网站的动态新闻数据库怎么做/推广专员
介绍求解P-中值问题的Matlab工具箱yalmip。

1
优化问题的建模与求解
现实生活中,有很多问题可以描述成优化问题,然后利用运筹优化的知识加以解决。它们通常遵循以下流程:
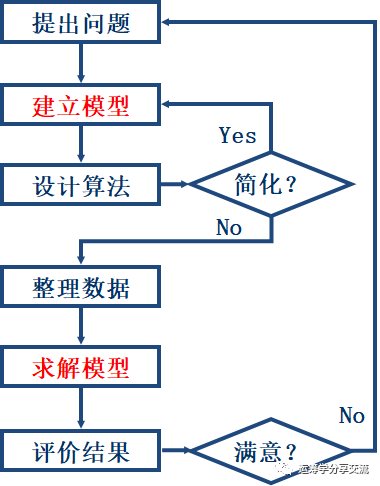
从上述流程中,可以看出,比较核心的两个步骤是:建模(modeling)和求解(solve)。
对于单纯形法,内点算法等成熟经典的运筹优化算法,现在有很多成熟的软件或者工具包,一般不需要自己去从头编程实现相应的算法。这些成熟的软件或者工具包,我们称之为求解器(solver)。常见的solver有lingo, cplex, gurobi, glpk,lpsolve, scip,matlab optimization toolbox等。
但是,实际问题成千上万万,它们的约束、目标等各不相同。如果要solver去适应不同问题,那么,它就没法干活了。因此,这些solver大都是针对比较通用标准的格式来编写算法,并对外提供接口。
不同的solver有不同的编程语言和接口,你想用不同的solver去求解同一个问题的时候,不得不去学习不同solver的专用语言,这就使得建模和求解即冗余又浪费精力。
比如,用matlab optimization toolbox求解LP问题,它的接口是:
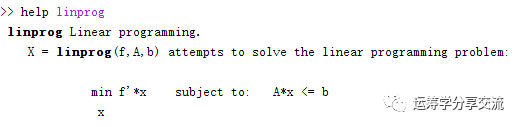
比如,使用 LPSolve解决线性规划问题,需要把所有约束显性地列出来。
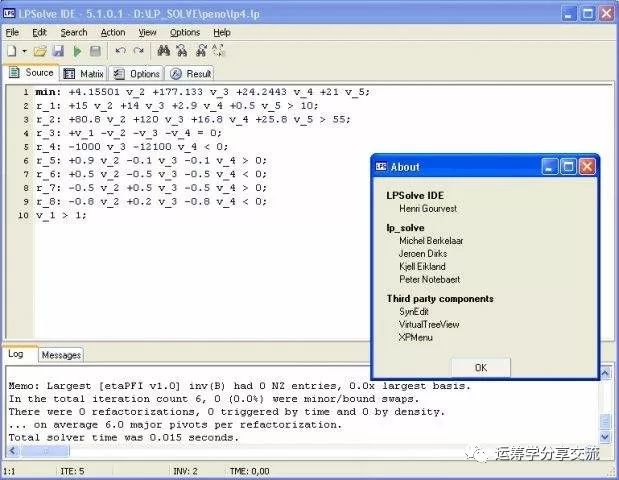
换句话说,要用上述两种solver求解LP问题,必须把约束系数矩阵A列出来。然而,很多实际问题的规模太大或者其他原因(如二维变量Xij),直接列出矩阵A是不太现实。但是,我们可以根据问题的数学模型,结合编程语言,使用for、if等建立所有的约束条件,这个过程就是在计算机层面实现对优化问题的“建模”。
那么,是否有一种方法,能够实现建模和求解的分离呢?也就是说,是否存在一种编程语言,可以对大部分的优化问题,用统一、简洁的建模语言来建模;然后,通过API或参数配置,调用不同的solver或自动选择合适的solver来求解。这类语言通常称为代数建模语言或优化建模语言。比如,AMPL,GNU MathProg, OPL,yalmip等。
2
yalmip概述
yalmip是由Johan Löfberg开发的一个免费开源的Matlab toolbox。虽然yalmip是matlab的一个toolbox,但更像是一个优化建模工具,或者说优化建模语言,通过它来统一建模,然后再调用其他solver来求解。
有了yalmip,我们不需要专门学习CPLEX、GUROBI、LINGO、GLPK、lpsolve等不同solver的建模语言,只需通过简单的参数配置或Matlab的API,即可实现对不同solver的调用,从而降低优化建模的学习难度。
3
yalmip的安装
yalmip的安装比较简单,可从https://yalmip.github.io/下载,并解压至matlab/toolbox或者你想要的路径,通过"设置路径"->“添加并包含子文件夹”来添加路径。
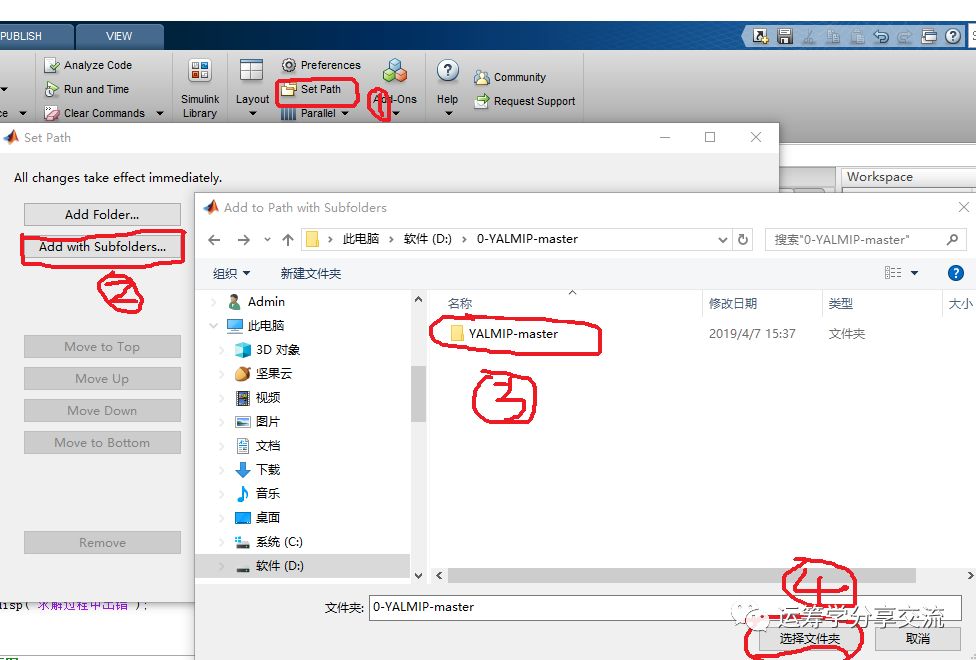
安装完yalmip,可以通过在命令行窗口中调用yalmitest,检查yalmip是否成功安装,并且可以查看yalmip所有支持的solver以及它们是否安装。
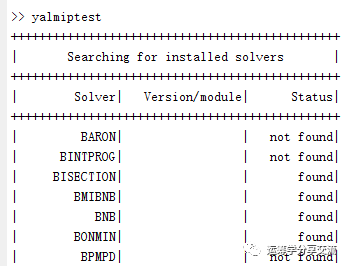
4
yalmip的使用
yalmip的建模比较简单,是与数学建模一致的。通常来讲,yalmip包含以下几个步骤。
4.1 决策变量
设置连续型变量:x = sdpvar(m, n, [option]),创建m*n的连续变量,option是一些参数设定
设置整数型变量:x = intvar(m, n, [option])
设置0-1型变量:x = binvar(m, n, [option])
X = sdpvar(1,2);4.2 约束条件
yalmip的约束条件比较简单、直接。比如,添加x1+x2<=1,x1>=x2
Constraint = [X(1)+X(2)<=1;X(1)-X(2)>=2];4.3 目标函数
yalmip的目标函数比较简单、直接。比如,要表达目标函数 z=x1+x2
Z = X(1)-2*X(2);4.4 参数设置
使用sdpsettings来设置参数,比如选定求解器(sovler),以及信息输出的级别(verbose)
在命令行中输入doc sdpsettings查看详细信息
ops = sdpsettings('verbose',2,'solver','scip');4.5 问题求解
yalmip默认求解min Z型问题。求max Z型问题,只需转换为min -Z即可
使用optimize(constraint,target,options)来调用
constraint:约束条件;target:目标函数;options:参数设置
sol = optimize(Constraint,Z,ops);feasible solution found by trivial heuristic after 0.0 seconds, objective value 2.000000e+05
presolving:
(round 1, fast) 0 del vars, 0 del conss, 0 add conss, 0 chg bounds, 0 chg sides, 0 chg coeffs, 1 upgd conss, 0 impls, 0 clqs
(round 2, fast) 1 del vars, 1 del conss, 0 add conss, 2 chg bounds, 0 chg sides, 0 chg coeffs, 1 upgd conss, 0 impls, 0 clqs
presolving (3 rounds: 3 fast, 1 medium, 1 exhaustive):
1 deleted vars, 1 deleted constraints, 0 added constraints, 2 tightened bounds, 0 added holes, 0 changed sides, 0 changed coefficients
0 implications, 0 cliques
presolved problem has 2 variables (0 bin, 0 int, 0 impl, 2 cont) and 2 constraints
2 constraints of type
Presolving Time: 0.00
transformed 1/1 original solutions to the transformed problem space
time | node | left |LP iter|LP it/n| mem |mdpt |frac |vars |cons |cols |rows |cuts |confs|strbr| dualbound | primalbound | gap
* 0.0s| 1 | 0 | 2 | - | 195k| 0 | - | 2 | 2 | 2 | 2 | 0 | 0 | 0 | 2.500000e+00 | 2.500000e+00 | 0.00
0.0s| 1 | 0 | 2 | - | 195k| 0 | - | 2 | 2 | 2 | 2 | 0 | 0 | 0 | 2.500000e+00 | 2.500000e+00 | 0.00
SCIP Status : problem is solved [optimal solution found]
Solving Time (sec) : 0.02
Solving Nodes : 1
Primal Bound : +2.50000000000000e+00 (2 solutions)
Dual Bound : +2.50000000000000e+00
Gap : 0.00 4.6 结果分析
分析结果是否有问题
if sol.problem== 0
solution = value(X) % 查看X的值
objective = value(Z) % 查看Z的值else
display('求解过程中出错');
sol.info
yalmiperror(sol.problem)endsolution =
1.5000 -0.5000
objective =
2.50004.7 其他命令
check: 检查约束条件是否满足
value: 查看变量或表达式的值
assign: 给变量调试赋值
5
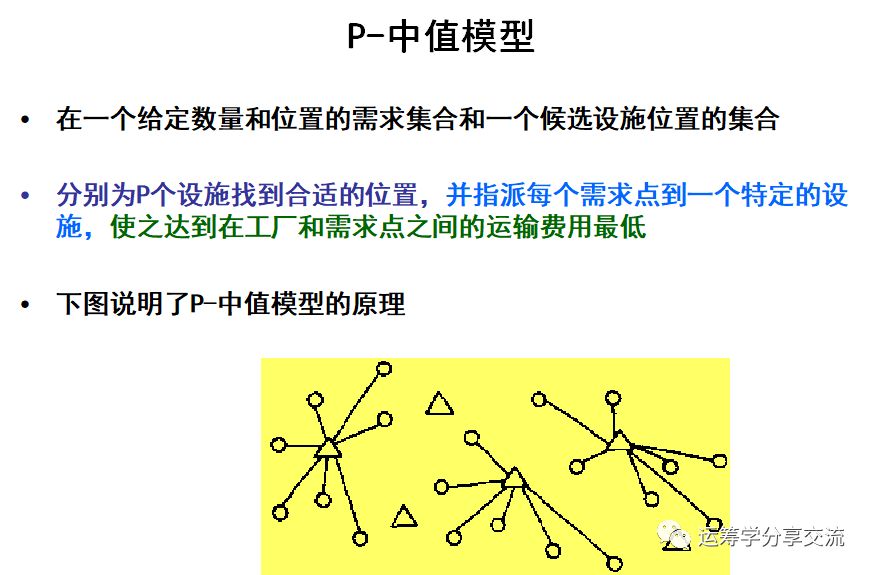
用yalmip求解P-中值问题
5.1 P-中值问题P-中值问题是指:在备选设施集合里,如何选择p个设施,使所有需求点得到服务,并且需求点到其最近设施的加权距离总和最小。


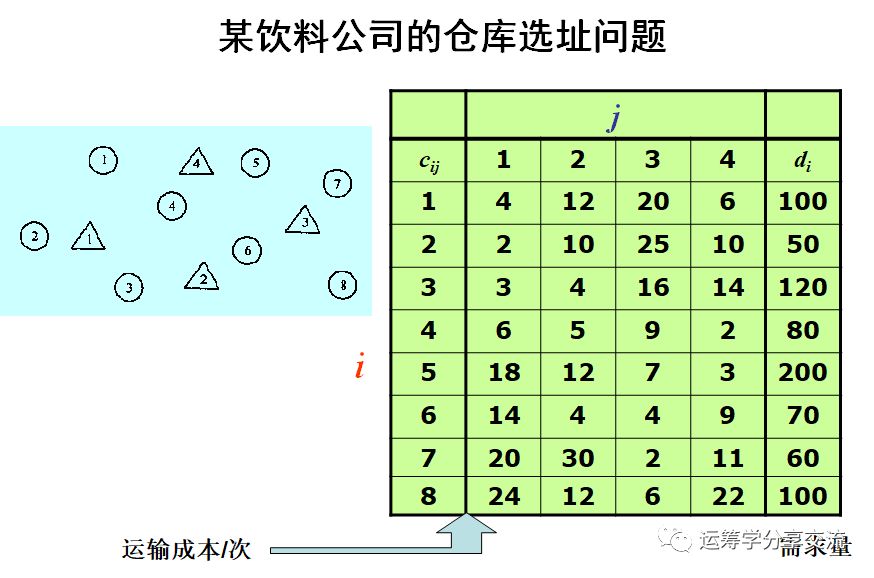
5.4 Matlab代码初始化
clc
cla
clf
clear all
close all添加路径
if isempty(which('sdpvar'))
yalmip_path = 'G:\0-YALMIP-master\YALMIP-master\' ; % yalmip toolbox的根目录
addpath(genpath(yalmip_path)) % yalmip toolbox的子目录end问题参数
data = [...
4 12 20 6 100;
2 10 25 10 50;
3 4 16 14 120;
6 5 9 2 80;
18 12 7 3 200;
14 4 4 9 70;
20 30 2 11 60;
24 12 6 22 100;
];
location = [...
14,38;
8,33;
13,30;
17,8;
22,15;
2,8;
23,1;
11,13;
10,28;
10,26;
7,22;
39,18]; % 需求点和候选设施点坐标
[nb_demand,n] = size(data); % nb_demand: 需求数量
nb_location = n -1; % nb_location: 候选设施数量
p = 2; % p: 待建设施数量
demand = data(:,end); % 需求数据
cost = data(:,1:nb_location); % 成本数据决策变量
X = binvar(nb_location,1,'full'); % Xj: 1,在候选点j建设施;0,不在候选点j建设施
Y = binvar(nb_demand,nb_location,'full'); % Yij: 1,需求点i由候选点j服务;0,需求点i不由候选点j服务目标函数
Z = 0;for i = 1:nb_demandfor j = 1:nb_location
Z = Z+demand(i)*cost(i,j)*Y(i,j);endend% Z= sum(demand.*sum(cost.*Y,2)); % 目标函数约束条件
Constraint = []; % 约束条件集合% 只有p个设施
Constraint=[Constraint,sum(X)==p];% 每个需求点只有一个设施服务for i=1:nb_demand
Constraint = [Constraint,sum(Y,2) == 1];end% 未被选中的候选设施不服务客户for i=1:nb_demandfor j=1:nb_location
Constraint=[Constraint,Y(i,j)<=X(j)]; % 每个城市都是出发地endend参数设置
ops = sdpsettings('verbose',2,'solver','scip'); % 调用开源SCIP solver 问题求解
sol = optimize(Constraint,Z,ops);% sol = solvesdp(Constraints,Z,ops);
if sol.problem== 0
value(X)
value(Z)else
disp('求解过程中出错');endpresolving:
(round 1, fast) 0 del vars, 0 del conss, 0 add conss, 0 chg bounds, 0 chg sides, 0 chg coeffs, 1 upgd conss, 0 impls, 40 clqs
(round 2, fast) 1 del vars, 1 del conss, 0 add conss, 2 chg bounds, 0 chg sides, 0 chg coeffs, 1 upgd conss, 0 impls, 40 clqs
(round 3, exhaustive) 1 del vars, 57 del conss, 0 add conss, 2 chg bounds, 0 chg sides, 0 chg coeffs, 1 upgd conss, 0 impls, 40 clqs
(round 4, exhaustive) 1 del vars, 57 del conss, 0 add conss, 2 chg bounds, 0 chg sides, 0 chg coeffs, 41 upgd conss, 0 impls, 40 clqs
(0.0s) probing cycle finished: starting next cycle
presolving (5 rounds: 5 fast, 3 medium, 3 exhaustive):
1 deleted vars, 57 deleted constraints, 0 added constraints, 2 tightened bounds, 0 added holes, 0 changed sides, 0 changed coefficients
0 implications, 40 cliques
presolved problem has 36 variables (36 bin, 0 int, 0 impl, 0 cont) and 41 constraints
40 constraints of type
1 constraints of type
transformed objective value is always integral (scale: 10)
Presolving Time: 0.01
time | node | left |LP iter|LP it/n| mem |mdpt |frac |vars |cons |cols |rows |cuts |confs|strbr| dualbound | primalbound | gap
T 0.0s| 1 | 0 | 0 | - | 395k| 0 | - | 36 | 41 | 36 | 41 | 0 | 0 | 0 | -- | 9.520000e+03 | Inf
* 0.0s| 1 | 0 | 22 | - | 391k| 0 | - | 36 | 41 | 36 | 41 | 0 | 0 | 0 | 3.740000e+03 | 3.740000e+03 | 0.00
0.0s| 1 | 0 | 22 | - | 391k| 0 | - | 36 | 41 | 36 | 41 | 0 | 0 | 0 | 3.740000e+03 | 3.740000e+03 | 0.00
SCIP Status : problem is solved [optimal solution found]
Solving Time (sec) : 0.01
Solving Nodes : 1
Primal Bound : +3.74000000000000e+03 (2 solutions)
Dual Bound : +3.74000000000000e+03
Gap : 0.00
ans =
1
0
1
0
ans =
3740结果展示
plot(location(1:nb_demand,1),location(1:nb_demand,2),'ro');
hold on;
plot(location(nb_demand+1:nb_demand+nb_location,1),location(nb_demand+1:nb_demand+nb_location,2),'bs');
hold on;for i=1:nb_demandfor j=1:nb_locationif value(Y(i,j))==1
plot([location(i,1),location(nb_demand+j,1)],[location(i,2),location(nb_demand+j,2)],'-g');endendend去除路径
if exist('yalmip_path','var')
rmpath(genpath(yalmip_path));endPublished with MATLAB® R2015b

