手机单页网站通用模板/站长之家域名解析

　　跟谁不会树链刨分一样 我也会。

树链刨分其实就是对树的每一条链都进行规划然后分轻重链。一般都是线段树维护的较多。

第一步 先求出这颗树的重儿子son[x] f[x] x节点的父亲 d[x] 节点的深度 size[x] 以x为根节点的儿子数

inline void dfs(int x,int father)
{d[x]=d[father]+1;f[x]=father;sz[x]=1;for(int i=lin[x];i;i=nex[i]){int tn=ver[i];if(tn==father)continue;dfs(tn,x);sz[x]+=sz[tn];if(sz[tn]>sz[son[x]])son[x]=tn;}return;
}

第二步 把重儿子轻儿子连成链 让链上的点连续加到线段树里好操作。

一般要求的是 top[x] x所在链的顶端 id[x] x的新编号 a[cnt] 在当前编号下的权值

inline void dp(int x,int father)
{id[x]=++cnt;a[cnt]=v[x];top[x]=father;if(son[x])dp(son[x],father);for(int i=lin[x];i;i=nex[i])if(tn!=father&&tn!=son[x])dp(tn,tn);
}

接下来是求LCA  例：求两点LCA 如果在同一条链上 显然输出深度较浅的那个即可。

如果不同 那其中一个top较深的向上跳不断的跳直到两点在同一链上此时输出深度小的即可。

关键是路径上的修改及查询 这个就是线段树维护路径进行区间修改了 这里的建树有一种动态开点般的建树。尽管没有什么用但是还是有点用的。

好吧 是有比较大的作用的空间能节省不少。 两倍空间还是可以省掉的。

第三步 对树上的链进行操作的话 树刨求LCA一下边往上跑边 在线段树进行修改。

查询时同理向上跳也进行和的累计、至于子树之内的直接线段树查询和线段树修改即可 因为他们的id号是连在一起的 然后调用就是

1 id[x] id[x]+sz[x]-1 z 这样进行子树->区间修改和查询即可。

//#include<bits/stdc++.h>
#include<iostream>
#include<iomanip>
#include<cmath>
#include<cstdio>
#include<ctime>
#include<queue>
#include<stack>
#include<vector>
#include<cctype>
#include<utility>
#include<algorithm>
#include<cstring>
#include<string>
#include<map>
#include<set>
#include<bitset>
#include<deque>
#include<cstdlib>
#define ll long long
#define db double
#define min(x,y) (x>y?y:x)
#define max(x,y) (x>y?x:y)
#define INF 2147483646
#define tn ver[i]
#define l(x) t[x].l
#define r(x) t[x].r
#define sum(x) t[x].sum
#define tag(x) t[x].tag
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline ll read()
{ll x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}return x*f;
}
inline void put(ll x)
{x<0?putchar('-'),x=-x:0;ll num=0;char ch[70];while(x)ch[++num]=x%10+'0',x/=10;num==0?putchar('0'):0;while(num)putchar(ch[num--]);putchar('\n');return;
}
const ll MAXN=100002;
ll n,m,root,mod,len,cnt;
ll lin[MAXN<<1],nex[MAXN<<1],ver[MAXN<<1];
ll v[MAXN],f[MAXN],sz[MAXN],son[MAXN],d[MAXN];
ll a[MAXN],id[MAXN],top[MAXN];
struct wy
{ll l,r,sum;ll tag;
}t[MAXN<<2];
inline void add(ll x,ll y)
{ver[++len]=y;nex[len]=lin[x];lin[x]=len;
}
inline void dfs(ll x,ll father)
{d[x]=d[father]+1;f[x]=father;sz[x]=1;for(ll i=lin[x];i;i=nex[i]){if(tn==father)continue;dfs(tn,x);sz[x]+=sz[tn];if(sz[tn]>sz[son[x]])son[x]=tn;}return;
}
inline void dp(ll x,ll father)
{id[x]=++cnt;a[cnt]=v[x];top[x]=father;if(!son[x])return;dp(son[x],father);for(ll i=lin[x];i;i=nex[i])if(tn!=f[x]&&tn!=son[x])dp(tn,tn);
}
inline void build(ll p,ll l,ll r)
{l(p)=l;r(p)=r;if(l==r){sum(p)=a[l];return;}ll mid=(l+r)>>1;build(p<<1,l,mid);build(p<<1|1,mid+1,r);sum(p)=(sum(p<<1)+sum(p<<1|1))%mod;return;
}
inline void pushdown(ll p)
{ll mid=(l(p)+r(p))>>1;sum(p<<1)=(sum(p<<1)+(mid-l(p)+1)*tag(p))%mod;sum(p<<1|1)=(sum(p<<1|1)+(r(p)-mid)*tag(p))%mod;tag(p<<1)=(tag(p<<1)+tag(p))%mod;tag(p<<1|1)=(tag(p<<1|1)+tag(p))%mod;tag(p)=0;return;
}
inline void change(ll p,ll l,ll r,ll k)
{if(l<=l(p)&&r>=r(p)){sum(p)=(sum(p)+(r(p)-l(p)+1)*k%mod)%mod;tag(p)=(tag(p)+k)%mod;return;}ll mid=(l(p)+r(p))>>1;if(tag(p))pushdown(p);if(l<=mid)change(p<<1,l,r,k);if(r>mid)change(p<<1|1,l,r,k);sum(p)=(sum(p<<1)+sum(p<<1|1))%mod;return;
}
inline void Tchange(ll x,ll y,ll z)
{ll fx=top[x],fy=top[y];while(fx!=fy){if(d[fx]<d[fy])swap(x,y),swap(fx,fy);change(1,id[fx],id[x],z);x=f[fx];fx=top[x];}if(d[x]<d[y])swap(x,y);change(1,id[y],id[x],z);return;
}
inline ll ask(ll p,ll l,ll r)
{if(l<=l(p)&&r>=r(p))return sum(p);ll mid=(l(p)+r(p))>>1;ll cnt=0;if(tag(p))pushdown(p);if(l<=mid)cnt=(cnt+ask(p<<1,l,r))%mod;if(r>mid)cnt=(cnt+ask(p<<1|1,l,r))%mod;return cnt;
}
inline ll Task(ll x,ll y)
{ll ans=0;ll fx=top[x],fy=top[y];while(fx!=fy){if(d[fx]<d[fy])swap(x,y),swap(fx,fy);ans=(ans+ask(1,id[fx],id[x]))%mod;x=f[fx];fx=top[x];}if(d[x]<d[y])swap(x,y);ans=(ans+ask(1,id[y],id[x]))%mod;return ans;
}
int main()
{//freopen("1.in","r",stdin);n=read();m=read();root=read();mod=read();for(ll i=1;i<=n;++i)v[i]=read()%mod;for(ll i=1;i<n;++i){ll x,y;x=read();y=read();add(x,y);add(y,x);}dfs(root,0);//for(ll i=1;i<=n;++i)put(son[i]);
    dp(root,root);build(1,1,cnt);for(ll i=1;i<=m;++i){ll p,x,y,z;p=read();switch(p){case 1:x=read();y=read();z=read();Tchange(x,y,z);break;case 2:x=read();y=read();put(Task(x,y));break;case 3:x=read();z=read();change(1,id[x],id[x]+sz[x]-1,z);break;case 4:x=read();put(ask(1,id[x],id[x]+sz[x]-1));break;}}return 0;
}

这道题可以利用上面的LCA做法成功解决。

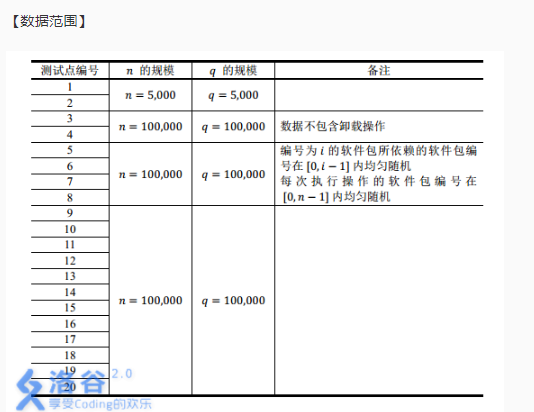
这道题询问的是 树上的某条链的状态和以某个为根的子树的状态。显然对于链直接求LCA 时更新。

对于以某个子树为根 我们可以直接在线段树中搞即可。查询和改变状态是一体的不必分开写，直接一起写了即可。省一倍常数。

//#include<bits/stdc++.h>
#include<iostream>
#include<iomanip>
#include<cmath>
#include<cstdio>
#include<ctime>
#include<queue>
#include<stack>
#include<vector>
#include<cctype>
#include<utility>
#include<algorithm>
#include<cstring>
#include<string>
#include<map>
#include<set>
#include<bitset>
#include<deque>
#include<cstdlib>
#define ll long long
#define db double
#define min(x,y) (x>y?y:x)
#define max(x,y) (x>y?x:y)
#define INF 2147483646
#define tn ver[i]
#define l(x) t[x].l
#define r(x) t[x].r
#define sum(x) t[x].sum
#define tag(x) t[x].tag
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}return x*f;
}
inline void put(int x)
{x<0?putchar('-'),x=-x:0;int num=0;char ch[70];while(x)ch[++num]=x%10+'0',x/=10;num==0?putchar('0'):0;while(num)putchar(ch[num--]);putchar('\n');return;
}
const int MAXN=100002;
int n,m,len,cnt;
int lin[MAXN],nex[MAXN],ver[MAXN];
int f[MAXN],top[MAXN],son[MAXN],d[MAXN];
int sz[MAXN],id[MAXN];
char a[15];
struct wy
{int l,r;int sum;int tag;
}t[MAXN<<2];
void add(int x,int y)
{ver[++len]=y;nex[len]=lin[x];lin[x]=len;
}
inline void dfs(int x,int father)
{d[x]=d[father]+1;sz[x]=1;f[x]=father;for(int i=lin[x];i;i=nex[i]){if(tn==father)continue;dfs(tn,x);sz[x]+=sz[tn];if(sz[tn]>sz[son[x]]||son[x]==0)son[x]=tn;}
}
inline void dp(int x,int father)
{id[x]=++cnt;top[x]=father;if(!son[x])return;dp(son[x],father);for(int i=lin[x];i;i=nex[i])if(tn!=f[x]&&tn!=son[x])dp(tn,tn);return;
}
inline void build(int p,int l,int r)
{l(p)=l;r(p)=r;if(l==r)return;int mid=(l+r)>>1;build(p<<1,l,mid);build(p<<1|1,mid+1,r);
}
inline void pushdown(int p)
{int mid=(l(p)+r(p))>>1;if(tag(p)==1){sum(p<<1)=(mid-l(p)+1);sum(p<<1|1)=(r(p)-mid);tag(p<<1)=tag(p<<1|1)=1;}else {sum(p<<1)=0;sum(p<<1|1)=0;tag(p<<1)=tag(p<<1|1)=-1;}tag(p)=0;return;
}
inline int askchange(int p,int l,int r,int k)
{int cnt=0;if(l<=l(p)&&r>=r(p)){cnt=((r(p)-l(p)+1)-sum(p));sum(p)=(r(p)-l(p)+1);tag(p)=k;return cnt;}int mid=(l(p)+r(p))>>1;if(tag(p))pushdown(p);if(l<=mid)cnt+=askchange(p<<1,l,r,k);if(r>mid)cnt+=askchange(p<<1|1,l,r,k);sum(p)=sum(p<<1)+sum(p<<1|1);return cnt;
}
inline int Tchange(int x)
{int ans=0;int fx=top[x],fy=top[0];while(fx!=fy){ans+=askchange(1,id[fx],id[x],1);x=f[fx];fx=top[x];}ans+=askchange(1,id[0],id[x],1);return ans;
}
inline int askmodify(int p,int l,int r,int k)
{int cnt=0;if(l<=l(p)&&r>=r(p)){cnt=sum(p);sum(p)=0;tag(p)=k;return cnt;}int mid=(l(p)+r(p))>>1;if(tag(p))pushdown(p);if(l<=mid)cnt+=askmodify(p<<1,l,r,k);if(r>mid)cnt+=askmodify(p<<1|1,l,r,k);sum(p)=sum(p<<1)+sum(p<<1|1);return cnt;
}
int main()
{//freopen("1.in","r",stdin);n=read();for(int i=1;i<n;++i){int x;x=read();add(x,i);}dfs(0,0);dp(0,0);//for(int i=0;i<n;++i)put(son[i]);build(1,1,cnt);m=read();for(int i=1;i<=m;++i){int x;scanf("%s",a+1);x=read();if(a[1]=='i')put(Tchange(x));else put(askmodify(1,id[x],id[x]+sz[x]-1,-1));}return 0;
}

并没有一次AC的原因1：线段树查询的时候l写成mid+1 r写成mid 

                                  2：查LCA时应该是id[0]而并非id[1]

                                  3: 线段树的区间仍应该是1到n并非0到n-1

这道题是一个很简单的链上的最大权值和权值和 和一个非常简单的单调修改。

我20min写完 发现样例过了 交了上去 发现AC了 码力还不错。

//#include<bits/stdc++.h>
#include<iostream>
#include<iomanip>
#include<cmath>
#include<cstdio>
#include<ctime>
#include<queue>
#include<stack>
#include<vector>
#include<cctype>
#include<utility>
#include<algorithm>
#include<cstring>
#include<string>
#include<map>
#include<set>
#include<bitset>
#include<deque>
#include<cstdlib>
#define ll long long
#define db double
#define INF 2147483646
#define tn ver[i]
#define l(x) t[x].l
#define r(x) t[x].r
#define sum(x) t[x].sum
#define w(x) t[x].w
#define maximum(x,y) (x>y?x:y)
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}return x*f;
}
inline void put(int x)
{x<0?putchar('-'),x=-x:0;int num=0;char ch[70];while(x)ch[++num]=x%10+'0',x/=10;num==0?putchar('0'):0;while(num)putchar(ch[num--]);putchar('\n');return;
}
const int MAXN=30002;
int n,m,len,cnt;
int lin[MAXN<<1],nex[MAXN<<1],ver[MAXN<<1];
int f[MAXN],top[MAXN],son[MAXN],d[MAXN];
int sz[MAXN],id[MAXN],a[MAXN],v[MAXN];
char b[10];
struct wy
{int l,r;int sum;int w;
}t[MAXN<<2];
inline int max(int x,int y){return x>y?x:y;}
void add(int x,int y)
{ver[++len]=y;nex[len]=lin[x];lin[x]=len;
}
inline void dfs(int x,int father)
{d[x]=d[father]+1;sz[x]=1;f[x]=father;for(int i=lin[x];i;i=nex[i]){if(tn==father)continue;dfs(tn,x);sz[x]+=sz[tn];if(sz[tn]>sz[son[x]])son[x]=tn;}
}
inline void dp(int x,int father)
{id[x]=++cnt;top[x]=father;a[cnt]=v[x];if(!son[x])return;dp(son[x],father);for(int i=lin[x];i;i=nex[i])if(tn!=f[x]&&tn!=son[x])dp(tn,tn);return;
}
inline void build(int p,int l,int r)
{l(p)=l;r(p)=r;if(l==r){sum(p)=a[l];w(p)=a[l];return;}int mid=(l+r)>>1;build(p<<1,l,mid);build(p<<1|1,mid+1,r);w(p)=maximum(w(p<<1),w(p<<1|1));sum(p)=sum(p<<1)+sum(p<<1|1);
}
inline void change(int p,int x,int k)
{if(l(p)==r(p)){sum(p)=k;w(p)=k;return;}int mid=(l(p)+r(p))>>1;if(x<=mid)change(p<<1,x,k);else change(p<<1|1,x,k);w(p)=maximum(w(p<<1),w(p<<1|1));sum(p)=sum(p<<1)+sum(p<<1|1);return;
}
inline int ask(int p,int l,int r)
{if(l<=l(p)&&r>=r(p))return w(p);int mid=(l(p)+r(p))>>1;int cnt=-INF;if(l<=mid)cnt=max(cnt,ask(p<<1,l,r));if(r>mid)cnt=max(cnt,ask(p<<1|1,l,r));return cnt;
}
inline int ask1(int p,int l,int r)
{if(l<=l(p)&&r>=r(p))return sum(p);int mid=(l(p)+r(p))>>1;int cnt=0;if(l<=mid)cnt+=ask1(p<<1,l,r);if(r>mid)cnt+=ask1(p<<1|1,l,r);return cnt;
}
inline int Task(int x,int y)
{int ans=-INF;int fx=top[x],fy=top[y];while(fx!=fy){if(d[fx]<d[fy])swap(x,y),swap(fx,fy);ans=max(ans,ask(1,id[fx],id[x]));x=f[fx];fx=top[x];}if(d[x]<d[y])swap(x,y);ans=max(ans,ask(1,id[y],id[x]));return ans;
}
inline int Task1(int x,int y)
{int ans=0;int fx=top[x],fy=top[y];while(fx!=fy){if(d[fx]<d[fy])swap(x,y),swap(fx,fy);ans+=ask1(1,id[fx],id[x]);x=f[fx];fx=top[x];}if(d[x]<d[y])swap(x,y);ans+=ask1(1,id[y],id[x]);return ans;
}
int main()
{//freopen("1.in","r",stdin);n=read();for(int i=1;i<n;++i){int x,y;x=read();y=read();add(x,y);add(y,x);}for(int i=1;i<=n;++i)v[i]=read();dfs(1,0);dp(1,1);build(1,1,cnt);m=read();for(int i=1;i<=m;++i){int x,y;scanf("%s",b+1);x=read();y=read();if(b[1]=='C')change(1,id[x],y);else{if(b[2]=='M')put(Task(x,y));else put(Task1(x,y));}}return 0;
}

这道题是一个树刨裸题当然树上差分也是可以做的因为只有一次区间询问。直接剖即可。

没有一次A的原因：1数组开小了 2 tag没有++而是等于1了。

//#include<bits/stdc++.h>
#include<iostream>
#include<iomanip>
#include<cmath>
#include<cstdio>
#include<ctime>
#include<queue>
#include<stack>
#include<vector>
#include<cctype>
#include<utility>
#include<algorithm>
#include<cstring>
#include<string>
#include<map>
#include<set>
#include<bitset>
#include<deque>
#include<cstdlib>
#define ll long long
#define db double
#define INF 2147483646
#define tn ver[i]
#define l(x) t[x].l
#define r(x) t[x].r
#define w(x) t[x].w
#define tag(x) t[x].tag
#define max(x,y) (x>y?x:y)
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}return x*f;
}
inline void put(int x)
{x<0?putchar('-'),x=-x:0;int num=0;char ch[70];while(x)ch[++num]=x%10+'0',x/=10;num==0?putchar('0'):0;while(num)putchar(ch[num--]);putchar('\n');return;
}
const int MAXN=50002;
int n,m,len,cnt;
int lin[MAXN<<1],nex[MAXN<<1],ver[MAXN<<1];
int f[MAXN],top[MAXN],son[MAXN],d[MAXN];
int sz[MAXN],id[MAXN];
struct wy
{int l,r;int w;int tag;
}t[MAXN<<2];
void add(int x,int y)
{ver[++len]=y;nex[len]=lin[x];lin[x]=len;
}
inline void dfs(int x,int father)
{d[x]=d[father]+1;sz[x]=1;f[x]=father;for(int i=lin[x];i;i=nex[i]){if(tn==father)continue;dfs(tn,x);sz[x]+=sz[tn];if(sz[tn]>sz[son[x]])son[x]=tn;}
}
inline void dp(int x,int father)
{id[x]=++cnt;top[x]=father;if(!son[x])return;dp(son[x],father);for(int i=lin[x];i;i=nex[i])if(tn!=f[x]&&tn!=son[x])dp(tn,tn);return;
}
inline void build(int p,int l,int r)
{l(p)=l;r(p)=r;if(l==r)return;int mid=(l+r)>>1;build(p<<1,l,mid);build(p<<1|1,mid+1,r);
}
inline void pushdown(int p)
{w(p<<1)+=tag(p);w(p<<1|1)+=tag(p);tag(p<<1)+=tag(p);tag(p<<1|1)+=tag(p);tag(p)=0;
}
inline void change(int p,int l,int r)
{if(l<=l(p)&&r>=r(p)){++w(p);++tag(p);return;}if(tag(p))pushdown(p);int mid=(l(p)+r(p))>>1;if(l<=mid)change(p<<1,l,r);if(r>mid)change(p<<1|1,l,r);w(p)=max(w(p<<1),w(p<<1|1));return;
}
inline void Tchange(int x,int y)
{int fx=top[x],fy=top[y];while(fx!=fy){if(d[fx]<d[fy])swap(x,y),swap(fx,fy);change(1,id[fx],id[x]);x=f[fx];fx=top[x];}if(d[x]<d[y])swap(x,y);change(1,id[y],id[x]);return;
}
int main()
{//freopen("1.in","r",stdin);n=read();m=read();for(int i=1;i<n;++i){int x,y;x=read();y=read();add(x,y);add(y,x);}dfs(1,0);dp(1,1);build(1,1,cnt);for(int i=1;i<=m;++i){int x,y;x=read();y=read();Tchange(x,y);}put(w(1));return 0;
}

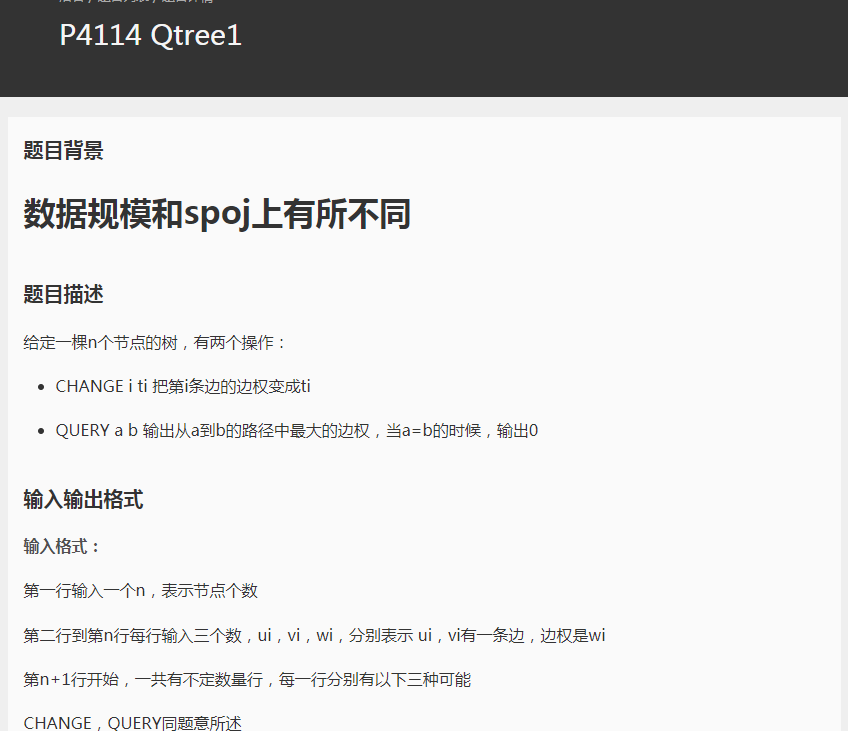
这道题还是一个树链刨分 不过 需要点边转换一下也不是很麻烦，记录好边的位置即可。

第一次没有AC的原因：while写成if 我是真的菜！！！我是个SB。

//#incldue<bits/stdc++.h>
#include<iostream>
#include<queue>
#include<iomanip>
#include<cctype>
#include<cstdio>
#include<deque>
#include<utility>
#include<cmath>
#include<ctime>
#include<cstring>
#include<string>
#include<cstdlib>
#include<vector>
#include<algorithm>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#define l(x) t[x].l
#define r(x) t[x].r
#define sum(x) t[x].sum
#define INF 2147483646
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}return x*f;
}
inline void put(int x)
{x<0?putchar('-'),x=-x:0;int num=0;char ch[50];while(x)ch[++num]=x%10+'0',x/=10;num==0?putchar('0'):0;while(num)putchar(ch[num--]);putchar('\n');return;
}
const int MAXN=100002;
int n,cnt,len;
int w[MAXN],d[MAXN],son[MAXN],b[MAXN],pos[MAXN];
int f[MAXN],sz[MAXN],top[MAXN],id[MAXN];
int lin[MAXN<<1],nex[MAXN<<1],ver[MAXN<<1],e[MAXN<<1];
char a[10];
struct wy
{int l,r;int sum;
}t[MAXN<<2];
inline int max(int x,int y){return x>y?x:y;}
inline void add(int x,int y,int z)
{ver[++len]=y;nex[len]=lin[x];lin[x]=len;e[len]=z;
}
inline void dfs(int x,int father)
{sz[x]=1;f[x]=father;d[x]=d[father]+1;for(int i=lin[x];i;i=nex[i]){int tn=ver[i];if(tn==father)continue;dfs(tn,x);w[tn]=e[i];pos[(i+1)>>1]=tn;sz[x]=sz[x]+sz[tn];if(sz[son[x]]<sz[tn])son[x]=tn;}
}
inline void dp(int x,int father)
{top[x]=father;id[x]=++cnt;b[cnt]=w[x];if(!son[x])return;dp(son[x],father);for(int i=lin[x];i;i=nex[i]){int tn=ver[i];if(tn!=f[x]&&tn!=son[x])dp(tn,tn);}return;
}
inline void build(int p,int l,int r)
{l(p)=l;r(p)=r;if(l==r){sum(p)=b[l];return;}int mid=(l+r)>>1;build(p<<1,l,mid);build(p<<1|1,mid+1,r);sum(p)=max(sum(p<<1),sum(p<<1|1));return;
}
inline void change(int p,int l,int k)
{if(l(p)==r(p)){sum(p)=k;return;}int mid=(l(p)+r(p))>>1;if(l<=mid)change(p<<1,l,k);else change(p<<1|1,l,k);sum(p)=max(sum(p<<1),sum(p<<1|1));
}
inline int ask(int p,int l,int r)
{if(l<=l(p)&&r>=r(p))return sum(p);int mid=(l(p)+r(p))>>1;int cnt=-INF;if(l<=mid)cnt=max(cnt,ask(p<<1,l,r));if(r>mid)cnt=max(cnt,ask(p<<1|1,l,r));return cnt;
}
inline int Task(int x,int y)
{int ans=-INF;int fx=top[x],fy=top[y];while(fx!=fy){if(d[fx]<d[fy])swap(x,y),swap(fx,fy);ans=max(ans,ask(1,id[fx],id[x]));x=f[fx];fx=top[x];}if(id[x]==id[y])return ans;if(d[x]<d[y])swap(x,y);ans=max(ans,ask(1,id[y]+1,id[x]));return ans;
}
int main()
{//freopen("1.in","r",stdin);n=read();for(int i=1;i<n;++i){int x,y,z;x=read();y=read();z=read();add(x,y,z);add(y,x,z);}dfs(1,0);dp(1,1);//for(int i=1;i<=n;++i)put(id[i]);//for(int i=1;i<=n;++i)put(b[id[i]]);build(1,1,cnt);while(1){int x,y;scanf("%s",a+1);if(a[1]=='D')break;x=read();y=read();if(a[1]=='C')change(1,id[pos[x]],y);if(a[1]=='Q'){if(x==y){puts("0");continue;}put(Task(x,y));}}return 0;
}

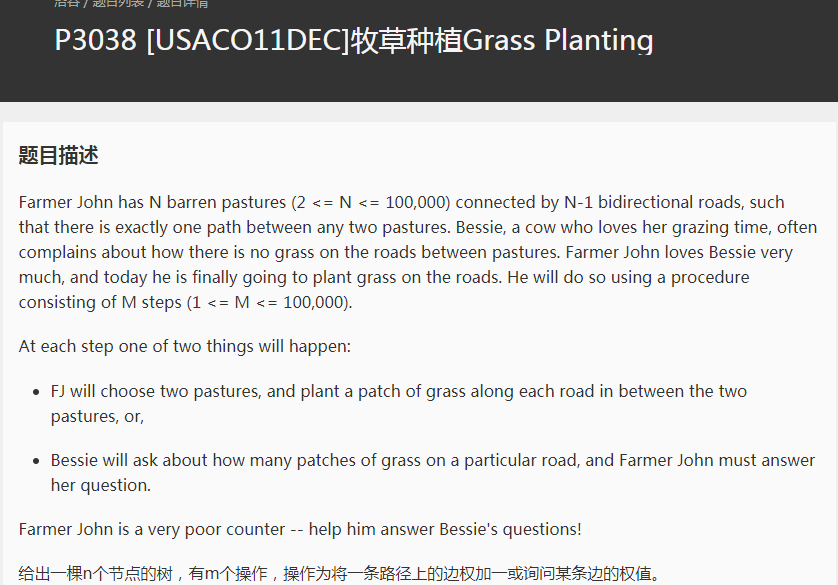
这道题就很简单了 是一个点边转换 后就是区间修改单点查询 可以直接线段树搞mlog^2n 复杂度不太优秀。

//#incldue<bits/stdc++.h>
#include<iostream>
#include<queue>
#include<iomanip>
#include<cctype>
#include<cstdio>
#include<deque>
#include<utility>
#include<cmath>
#include<ctime>
#include<cstring>
#include<string>
#include<cstdlib>
#include<vector>
#include<algorithm>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#define l(x) t[x].l
#define r(x) t[x].r
#define sum(x) t[x].sum
#define INF 2147483646
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}return x*f;
}
inline void put(int x)
{x<0?putchar('-'),x=-x:0;int num=0;char ch[50];while(x)ch[++num]=x%10+'0',x/=10;num==0?putchar('0'):0;while(num)putchar(ch[num--]);putchar('\n');return;
}
const int MAXN=100002;
int n,m,cnt,len;
int d[MAXN],son[MAXN];
int f[MAXN],sz[MAXN],top[MAXN],id[MAXN];
int lin[MAXN<<1],nex[MAXN<<1],ver[MAXN<<1];
char a[2];
struct wy
{int l,r;int sum;//既是值也是mark
}t[MAXN<<2];
inline int max(int x,int y){return x>y?x:y;}
inline void add(int x,int y)
{ver[++len]=y;nex[len]=lin[x];lin[x]=len;
}
inline void dfs(int x,int father)
{sz[x]=1;f[x]=father;d[x]=d[father]+1;for(int i=lin[x];i;i=nex[i]){int tn=ver[i];if(tn==father)continue;dfs(tn,x);sz[x]=sz[x]+sz[tn];if(sz[son[x]]<sz[tn])son[x]=tn;}
}
inline void dp(int x,int father)
{top[x]=father;id[x]=++cnt;if(!son[x])return;dp(son[x],father);for(int i=lin[x];i;i=nex[i]){int tn=ver[i];if(tn!=f[x]&&tn!=son[x])dp(tn,tn);}return;
}
inline void build(int p,int l,int r)
{l(p)=l;r(p)=r;if(l==r)return;int mid=(l+r)>>1;build(p<<1,l,mid);build(p<<1|1,mid+1,r);return;
}
inline void pushdown(int p)
{sum(p<<1)+=sum(p);sum(p<<1|1)+=sum(p);sum(p)=0;return;
}
inline void change(int p,int l,int r)
{if(l<=l(p)&&r>=r(p)){++sum(p);return;}if(sum(p))pushdown(p);int mid=(l(p)+r(p))>>1;if(l<=mid)change(p<<1,l,r);if(r>mid)change(p<<1|1,l,r);return;
}
inline int ask(int p,int l)
{if(l(p)==r(p))return sum(p);int mid=(l(p)+r(p))>>1;if(sum(p))pushdown(p);if(l<=mid)return ask(p<<1,l);else return ask(p<<1|1,l);
}
inline void Tchange(int x,int y)
{int fx=top[x],fy=top[y];while(fx!=fy){if(d[fx]<d[fy])swap(x,y),swap(fx,fy);change(1,id[fx],id[x]);x=f[fx];fx=top[x];}if(id[x]==id[y])return;if(d[x]<d[y])swap(x,y);change(1,id[y]+1,id[x]);
}
int main()
{//freopen("1.in","r",stdin);n=read();m=read();for(int i=1;i<n;++i){int x,y;x=read();y=read();add(x,y);add(y,x);}dfs(1,0);dp(1,1);//for(int i=1;i<=n;++i)put(id[i]);//for(int i=1;i<=n;++i)put(b[id[i]]);build(1,1,cnt);for(int i=1;i<=m;++i){int x,y;scanf("%s",a+1);x=read();y=read();if(a[1]=='P')Tchange(x,y);if(a[1]=='Q'){if(id[x]<id[y])swap(x,y);put(ask(1,id[x]));}}return 0;
}

一次AC了。

当然我其实是直接想树上差分 求LCA计算贡献如何计算呢 考虑树状数组 先对这棵树进行规划 直接dfs序即可然后差分的进行 即可。

但是这是不支持区间查询的 而树刨支持哦。线段树dfs序也是可以的不过需要差分一下线段树然后就没了。

其实这些只要不卡常树刨都能写而且维护的东西还更多。dfs序的特点是出和进都是可控的 不懂得话可画图模拟。

搞了半天 这些讨论的都没有什么意义和价值 不妨直接硬上树刨吧。

这道题 被我秒了 其实就是区间修改罢了。

//#incldue<bits/stdc++.h>
#include<iostream>
#include<queue>
#include<iomanip>
#include<cctype>
#include<cstdio>
#include<deque>
#include<utility>
#include<cmath>
#include<ctime>
#include<cstring>
#include<string>
#include<cstdlib>
#include<vector>
#include<algorithm>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#define l(x) t[x].l
#define r(x) t[x].r
#define sum(x) t[x].sum
#define INF 2147483646
#define tn ver[i]
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}return x*f;
}
inline void put(int x)
{x<0?putchar('-'),x=-x:0;int num=0;char ch[50];while(x)ch[++num]=x%10+'0',x/=10;num==0?putchar('0'):0;while(num)putchar(ch[num--]);putchar('\n');return;
}
const int MAXN=300002;
int n,m,len,cnt;
int lin[MAXN<<1],nex[MAXN<<1],ver[MAXN<<1];
int f[MAXN],top[MAXN],son[MAXN],d[MAXN],a[MAXN];
int sz[MAXN],id[MAXN],ans[MAXN],pos[MAXN];
struct wy
{int l,r;int sum;
}t[MAXN<<2];
void add(int x,int y)
{ver[++len]=y;nex[len]=lin[x];lin[x]=len;
}
inline void dfs(int x,int father)
{d[x]=d[father]+1;sz[x]=1;f[x]=father;for(int i=lin[x];i;i=nex[i]){if(tn==father)continue;dfs(tn,x);sz[x]+=sz[tn];if(sz[tn]>sz[son[x]])son[x]=tn;}
}
inline void dp(int x,int father)
{id[x]=++cnt;pos[cnt]=x;top[x]=father;if(!son[x])return;dp(son[x],father);for(int i=lin[x];i;i=nex[i])if(tn!=f[x]&&tn!=son[x])dp(tn,tn);return;
}
inline void build(int p,int l,int r)
{l(p)=l;r(p)=r;if(l==r)return;int mid=(l+r)>>1;build(p<<1,l,mid);build(p<<1|1,mid+1,r);
}
inline void pushdown(int p)
{sum(p<<1)+=sum(p);sum(p<<1|1)+=sum(p);sum(p)=0;return;
}
inline void change(int p,int l,int r)
{if(l<=l(p)&&r>=r(p)){++sum(p);return;}if(sum(p))pushdown(p);int mid=(l(p)+r(p))>>1;if(l<=mid)change(p<<1,l,r);if(r>mid)change(p<<1|1,l,r);return;
}
inline void Tchange(int x,int y)
{int fx=top[x],fy=top[y];while(fx!=fy){if(d[fx]<d[fy])swap(x,y),swap(fx,fy);change(1,id[fx],id[x]);x=f[fx];fx=top[x];}if(d[x]<d[y])swap(x,y);change(1,id[y],id[x]);return;
}
inline void modify(int p,int l,int r)
{if(l==r){ans[pos[l]]+=sum(p);return;}int mid=(l+r)>>1;if(sum(p))pushdown(p);modify(p<<1,l,mid);modify(p<<1|1,mid+1,r);return;
}
int main()
{//freopen("1.in","r",stdin);n=read();for(int i=1;i<=n;++i)a[i]=read();for(int i=1;i<n;++i){int x,y;x=read();y=read();add(x,y);add(y,x);}++ans[a[1]];--ans[a[n]];dfs(1,0);dp(1,1);build(1,1,cnt);for(int i=1;i<n;++i)//最后一个地点不用加考虑加的区间为[a[i],a[i+1])直接在答案数组中减去即可。--ans[a[i]],Tchange(a[i],a[i+1]);modify(1,1,cnt);for(int i=1;i<=n;++i)put(ans[i]);return 0;
}

一遍AC 码力不错 写的时候有点慌一些地方一直调错。

值得一提的是此题完全没有必要树刨+线段树 直接LCA+树上差分即可。（复杂度更优秀）果然数据结构学傻人。

忆对中秋丹桂丛。花在杯中。月在杯中。