教育课程网站建设/湛江seo推广外包

期末考完来复健辣

A. Polycarp and the Day of Pi

给出一串π的数字，判断从前向后数连续几位是正确的。

思路：题目说明最多30位，然后样例很贴心的给了一个30位的，那就直接贴过来遍历判断就好啦！

AC Code：

#include <bits/stdc++.h>typedef long long ll;
const int N = 1e5 + 5;
int t;
std::string s;int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);std::cin >> t;while(t --) {std::cin >> s;std::string ans = "314159265358979323846264338327";int pos = -1;for(int i = 0; i < std::min(s.length(), ans.length()); i ++) {if(s[i] != ans[i]) {pos = i;break;}}if(pos == -1)pos = s.length();std::cout << pos << '\n';}return 0;
}

B. Taisia and Dice

有一个具有n个数字的数组，每一个数字都小于等于6，给出所有数字的和和随即去掉一个数后数组的和，构造一个满足条件的数组。

思路：有一个数不能动，就是去掉的数，这个数的大小是确定的；剩下的和，平均数给剩下的n-1个数，余数遍历加上即可。

AC Code：

#include <bits/stdc++.h>typedef long long ll;
const int N = 1e5 + 5;
int t, n, s, r;
int a[N];int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);std::cin >> t;while(t --) {std::cin >> n >> s >> r;a[0] = s - r;int res = r % (n - 1);for(int i = 1; i < n; i ++) {a[i] = r / (n - 1);if(res)a[i] ++, res --;}for(int i = 0; i < n; i ++) {std::cout << a[i] << " \n"[i == n - 1];}}return 0;
}

C. Premutation

给出n个具有n-1个数的数组，每个数组都是原数组随机去掉一个位置的数剩下的，且每个位置恰好去掉过一次，根据给出的n个数组，求原数组。

思路：因为每个数组都是仅去掉一个数的，只要找出第一个数是什么，然后加上后面的数即可。

AC Code：

#include <bits/stdc++.h>typedef long long ll;
const int N = 105;
int t, n;
int a[N][N], cnt[N];int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);std::cin >> t;while(t --) {std::cin >> n;for(int i = 1; i <= n; i ++)cnt[i] = 0;for(int i = 1; i <= n; i ++) {for(int j = 1; j < n; j ++) {std::cin >> a[i][j];}}int pos;for(int i = 1; i <= n; i ++) {cnt[a[i][1]] ++;if(cnt[a[i][1]] > 1) {pos = a[i][1];break;}}std::cout << pos;for(int i = 1; i <= n; i ++) {if(a[i][1] != pos) {pos = i;break;}}for(int i = 1; i < n; i ++) {std::cout << ' ' << a[pos][i]; }std::cout << '\n';}return 0;
}

D. Matryoshkas

给出n个数，每一段都由连续的数组成，求最少有多少段数。

思路：对于不相连的数，每一连续数段的贡献是个数最多的那个数，但是也有种情况需要注意，即1 1 2 3 3这种情况，3不能与前面直接计算，特别判断即可。

AC Code：

#include <bits/stdc++.h>typedef long long ll;
typedef std::pair<int, int> PII;
const int N = 2e5 + 5;
int t, n;
int a[N];int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);std::cin >> t;while(t --) {std::cin >> n;std::map<int, int> mp;std::vector<PII> vec;for(int i = 1; i <= n; i ++) {std::cin >> a[i];mp[a[i]] ++;}for(auto [x, y] : mp) {PII b = std::make_pair(x, y);vec.push_back(b);}std::sort(vec.begin(), vec.end());int len = vec.size();ll ans = 0;int max = vec[0].second;for(int i = 1; i < len; i ++) {if(vec[i].first == vec[i - 1].first + 1 && max >= vec[i - 1].second && vec[i].second > vec[i - 1].second)ans += max - vec[i - 1].second, max = vec[i].second;else if(vec[i].first == vec[i - 1].first + 1)max = std::max(max, vec[i].second);elseans += max, max = vec[i].second;}ans += max;std::cout << ans << '\n';}return 0;
}

os：特殊情况条件判错了wa了一发QAQ

E. Vlad and a Pair of Numbers

给出一个数x，求满足a xor b = (a + b) / 2 = x的任意一组a和b，注意其中的除以2不是取整。

思路：根据题意，可以得到的条件是a + b = x * 2，a xor b = x，那么x二进制下的为1的位必须只有一个数有。那剩下的x，必须一个数一半体现在数中，且这一半的二进制位是1的不能与x是1的位置重合。当然，x不是偶数时，直接判断-1即可。

AC Code：

#include <bits/stdc++.h>typedef long long ll;
const int N = 35;
int t, x;
int cnt[N];int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);std::cin >> t;while(t --) {std::cin >> x;for(int i = 1; i <= 31; i ++) {cnt[i] = 0;if(x >> (i - 1) & 1)cnt[i] ++;}if(x & 1) {std::cout << -1 << '\n';continue;}int h = x >> 1;bool flag = true;for(int i = 1; i <= 31; i ++) {if((h >> (i - 1) & 1) && cnt[i]) {flag = false;break;}}if(!flag) {std::cout << -1 << '\n';continue;}std::cout << x + (x / 2) << ' ' << x / 2 << '\n';}return 0;
}

F. Timofey and Black-White Tree

给出一棵树，其中c点为黑色，其他点为白色，现在要将其中所有的白点染成黑色，每次选择一个白点，求每次染完色后的树的正值。正值是指最近的两个黑色点之间的距离。

思路：可以考虑对于每个点直接BFS求最短路。对于复杂度的可行性，可以这样理解：对于每一个点求最短路，因为若是每次路程最大，那最后应该是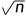次染色，即最多是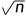次扩展，而对于这样，每次更新节点dis值都会至少减少1，所以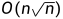的复杂度，完全可以通过。

解释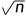：例如1 2 3 4 5 6 7连成一条线的情况，最多次数是先1,7，后如果还要保证染色次数最多，那必然是3，这样求的。

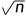AC Code：

#include <bits/stdc++.h>typedef long long ll;
#define INF 0x3f3f3f3f
const int N = 2e5 + 5;
int t, n;
int a[N], dis[N];
std::vector<int> vec[N];int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);std::cin >> t;while(t --) {std::cin >> n >> a[1];for(int i = 1; i <= n; i ++) {vec[i].clear();dis[i] = INF;}for(int i = 2; i <= n; i ++) {std::cin >> a[i];}for(int i = 1; i < n; i ++) {int u, v;std::cin >> u >> v;vec[u].push_back(v);vec[v].push_back(u);}int ans = INF;for(int i = 1; i <= n; i ++) {ans = std::min(ans, dis[a[i]]);if(i > 1)std::cout << ans << " \n"[i == n];std::queue<int> q;q.push(a[i]);dis[a[i]] = 0;while(!q.empty()) {int now = q.front();q.pop();for(auto x : vec[now]) {if(dis[now] + 1 < dis[x] && dis[now] + 1 <= ans) {dis[x] = dis[now] + 1;q.push(x);}}}}}return 0;
}