当前位置：首页 > news >正文

微网站制作工具有哪些/深圳推广公司哪家最好

news 2025/6/30 7:05:11

微网站制作工具有哪些,深圳推广公司哪家最好,python基础教程人民邮电出版社,wordpress 客服线性分类相关文章： 1、Fisher线性判别分析(LDA)[1]2、广义模型与线性模型& 判别分析 [2]3、逻辑回归[3]4、线性分类模型简介5、感知机原理及代码复现6、概率生成模型本文主要包含以下内容： 1 简介2 固定基函数3 逻辑回归4 迭代加权最小二乘5 多类逻辑…

线性分类相关文章： 1、Fisher线性判别分析(LDA)^[1]2、广义模型与线性模型& 判别分析 ^[2]3、逻辑回归^[3]4、线性分类模型简介5、感知机原理及代码复现6、概率生成模型

本文主要包含以下内容：

1 简介
2 固定基函数
3 逻辑回归
4 迭代加权最小二乘
5 多类逻辑回归
6 概率单位回归
7 规范的链接函数

1 简介

对于二分类问题，我们已经看到，对于类条件分布的广泛选择，类的后验概率可以写成作用于的线性函数的logistic sigmoid函数。

同样，对于多类的情况，类的后验概率是线性函数的softmax变换。对于类条件密度的具体选择，我们使用最大似然来确定密度的参数以及类先验，然后使用贝叶斯定理找到类后验概率。

然而，另一种方法是明确地使用广义线性模型的函数形式，并用最大似然法直接确定其参数。我们将看到，有一种有效寻找这样的解的算法称为迭代重加权最小二乘(iterative reweighted least squares)，或IRLS。

间接来找到一个广义线性模型的参数的方法，通过拟合类条件密度和类先验分开，然后应用贝叶斯定理，代表生成(generative)模型的一个例子，因为我们可能需要这样一个模型并通过从边际分布中抽取的值生成合成数据。

在直接方法中，我们最大化一个通过条件分布定义的似然函数，它代表了一种判别(discriminative)训练的形式。

判别方法的一个优点是，通常需要确定的自适应参数更少，稍后我们将看到这一点。它还可能改进预测性能，特别是当类条件密度的假设给出一个接近真实分布的较差近似。

2 固定基函数

到目前为止，已经考虑了直接与原始输入向量一起工作的分类模型。但如果首先使用向量的基函数对输入进行固定的非线性转换，那么所有的算法都同样适用。所产生的决策边界在特征空间中是线性的，它们对应于原始空间中的非线性决策边界，如图12所示。

类在特征空间中是线性可分，不需要在原始观测空间中线性可分。在讨论线性回归模型，其中一个基函数通常设置为一个常数，即，所以相应的参数扮演偏差角色。

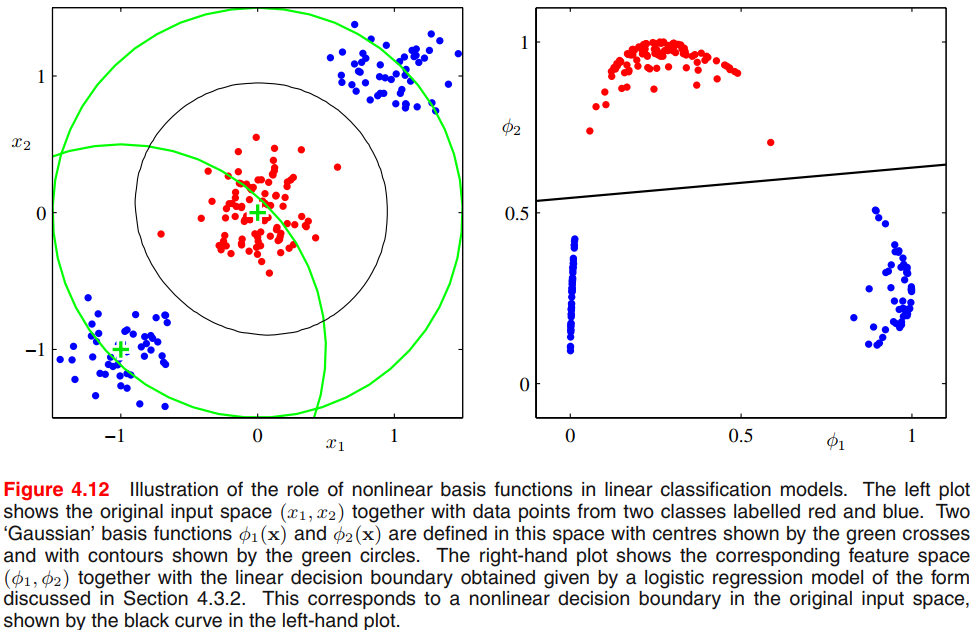
在许多实际问题中，类条件密度之间存在明显的重叠。这对应于后验概率至少对于的某些值不为0或1。在这种情况下，通过对后验概率进行精确建模，然后应用标准决策理论来获得最优解。

非线性转换，不能删除类重叠。事实上，它们可以增加重叠的程度，或者在原始观测空间中不存在的地方创造重叠。但适当的非线性选择可以使后验概率建模过程更容易。

这种固定的基函数模型有重要的限制，这些将在后面的文章中通过允许基函数本身适应数据来解决。尽管有这些限制，具有固定非线性基函数的模型在应用中扮演着重要的角色，并且对这种模型的讨论将引入许多关键的概念，以便理解它们更复杂的对等物。

3 逻辑回归

从考虑二分类问题开始处理广义线性模型。在关于生成方法的讨论中，我们看到在相当一般的假设下，类的后验概率可以写成作用于特征向量的线性函数的logistic sigmoid，因此：

。这里的是式59定义的logistic sigmoid函数。在统计学术语中，这种模型称为逻辑回归，但应强调这是一种分类模型，而不是回归模型。

对于一个维的特征空间，该模型具有个可调参数。相比之下，如果使用最大似然来拟合高斯类条件密度，对于均值将使用个参数，对于(共享)协方差矩阵将用。与类先验一起，它给出了个参数的总数，这些参数与成 二次增长，与逻辑回归中参数数量对的线性依赖形成对比。对于较大的值，直接使用logistic回归模型有明显的优势。

我们现在使用最大似然来确定logistic回归模型的参数。为了做到这一点，我们将利用logistic sigmoid函数的导数，它可以方便地用sigmoid函数本身来表示：

式

对于数据集，其中，，，似然函数可以写为：

其中，。通常，我们可以通过对概率取负对数来定义一个误差函数，从而得到交叉熵(cross entropy)误差函数的形式：

其中，，取误差函数关于的梯度，得到：

使用了式88。可以看到，涉及logistic sigmoid的导数的因子已经被消除，导致对数似然的梯度的简化形式。特别是，数据点对梯度的贡献是由目标值与模型的预测之间的误差乘以基函数向量给出的。与式13的比较表明，它与线性回归模型的平方和误差函数的梯度具有完全相同的形式。

如果需要，我们可以利用结果式91来给出一个顺序算法，其中模式一次只给出一个，其中每个权向量都使用式22更新，其中是式91中的第项。

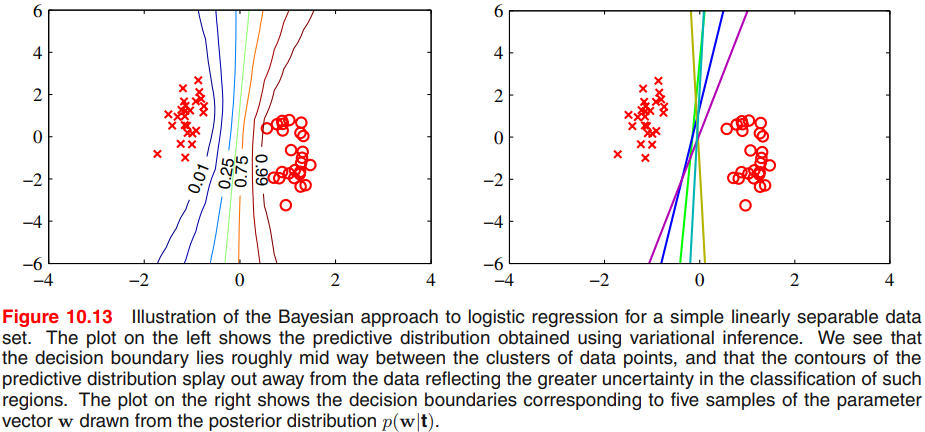
值得注意的是，对于线性可分离的数据集，最大似然可能表现出严重的过拟合。这是因为最大似然解出现在对应于的超平面上，相当于，将两类分离，的大小趋于无穷时。在这种情况下，logistic sigmoid函数在特征空间中变得无限陡峭，对应一个Heaviside阶跃函数，从而使每个类的每个训练点的后验概率。

此外，这些解通常是连续的，因为任何分离的超平面都会在训练数据点上产生相同的后验概率，如图10.13所示。最大似然性并不能使一个解决方案优于另一个解决方案，在实践中找到哪种解决方案将取决于优化算法的选择和参数初始化。需要注意的是，即使数据点的数量比模型中的参数的数量大，只要训练数据集是线性可分的，问题就会出现。奇异点可以通过包含一个先验和为找到一个映射解决方案来避免，或者等效地通过增加一个正则化项到误差函数。

4 迭代加权最小二乘

在线性回归模型的情况下，在高斯噪声模型的假设下的最大似然解导致一个封闭形式的解。这是对数似然函数对参数向量的二次依赖的结果。

对于logistic回归，由于logistic sigmoid函数的非线性，不再有一个封闭形式的解。但对二次型的背离并不明显。准确地说，误差函数是凹的，因此有唯一的最小值。

此外，利用对对数似然函数局部二次逼近的Newton-Raphson迭代优化方案，可以有效地最小化误差函数。最小化函数的Newton-Raphson更新形式为：

其中是Hessian矩阵，其元素包含对分量的二阶导数。

首先，将Newton-Raphson方法应用于具有平方和误差函数(式12)的线性回归模型(式3)。该误差函数的梯度和Hessian为：

式中是的设计矩阵，其第行由给出。则Newton Raphson的更新形式为：

我们认为它是标准的最小二乘解。在这种情况下，误差函数是二次的，因此Newton Raphson公式一步就给出了精确解。

现在让我们对logistic回归模型的交叉熵误差函数式90应用Newton-Raphson更新。由式91我们可以看到，这个误差函数的梯度和Hessian为：

使用了式88。同时，引入了的对角矩阵，其元素为：

式

可以看到，Hessian不再是常数，而是通过加权矩阵依赖于，这与误差函数不再是二次的事实相对应。使用属性，由logistic sigmoid函数的形式可知，对于任意向量有，所以Hessian矩阵是正定的。由此可以得出，误差函数是的凸函数，因此有唯一的最小值。

logistic回归模型的Newton-Raphson更新公式变为：

其中是维向量，其元素为：

可以看到，更新公式式99采用加权最小二乘的正规方程形式。因为权重矩阵不是恒定的，而是取决于参数向量，我们必须迭代地应用正规方程，每次使用新的权向量计算修订权重矩阵。由于这个原因，该算法被称为迭代重加权最小二乘(iterative reweighted least squares)，或IRLS。与加权最小二乘问题一样，对角加权矩阵的元素可以解释为方差，因为logistic回归模型中的均值和方差为：

这里使用了的属性。事实上，可以将IRLS解释为变量空间中线性化问题的解。对应于的第个元素的量可以被简单地解释为该空间的有效目标值，该目标值是通过在当前工作点附近对logistic sigmoid函数进行局部线性逼近而得到的：

5 多类逻辑回归

在对多类生成模型的讨论中，对于类分布后验概率是由特征变量的线性函数的softmax变换给出的，因此：

式中激活为：

式

利用极大似然分别确定类条件密度和类先验，然后利用贝叶斯定理找到相应的后验概率，从而隐式确定参数。这里考虑使用极大似然直接确定该模型的参数。要做到这一点，我们需要对所有激活的导数，即：

式中是单位矩阵元素。

接下来我们写下似然函数。最容易做到的是使用编码方案，其中属于类的特征向量的目标向量是一个二进制向量，除元素等于1外，其它元素都为零，则似然函数为：

式中，是的目标矩阵，矩阵元素为。则取负对数得到：

这被称为多类问题的交叉熵(cross-entropy)误差函数。

我们现在采取误差函数对每个参数向量的梯度。利用 softmax函数的导数结果式106，得到：

式中利用了。再一次，我们看到梯度的形式与线性模型的平方和误差函数和logistic回归模型的交叉熵误差的形式相同，即误差乘以基函数的乘积。同样，我们可以使用它来制定一个顺序算法，在这个算法中，模式一次呈现一个，其中每个权值向量都使用式22来更新。

我们已经看到，对于一个数据点，线性回归模型的对数似然函数对参数向量的导数采用误差乘以特征向量的形式。同样，对于logistic sigmoid激活函数与交叉熵误差函数式90的组合，以及softmax激活函数与多类交叉熵误差函数式108的组合，我们再次得到了同样简单的形式。这是一个更一般的结果的例子。

为了找到一个批处理算法，我们再次求助于Newton-Raphson更新来得到对应的多类问题的IRLS算法。这需要计算由大小为的块组成的Hessian矩阵，其中块为：

与二类问题一样，多类logistic回归模型的Hessian矩阵是正定的，因此误差函数具有唯一的最小值。

6 概率单位回归

已经看到，对于由指数族描述的广泛的类条件分布，后验类概率的结果由作用于特征变量的线性函数的logistic(或softmax)变换给出。但并不是所有的类条件密度的选择都能产生简单形式的后验概率(例如如果使用高斯混合模型来对类条件密度建模)。这表明，其他类型的判别概率模型值得探索。但我们将回到两类的情况，并再次保持在广义线性模型的框架内，因此：

式

式中，是激活函数。

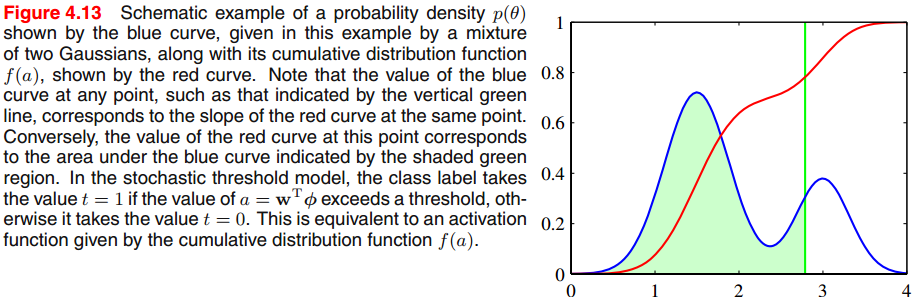
对链接函数激励一个替换选择的方法是考虑一个噪声阈值模型，如下所示。对于每一个输入，计算，然后根据下面的公式设定目标值：

如果的值是从概率密度中抽取的，则相应的激活函数将由累积分布函数给出：

式

正如图13所示。

作为一个具体的例子，假设密度是由一个零均值，单位方差的高斯给出。其累积分布函数为：

式

这被称为probit函数。它呈s形，并与图9中的logistic sigmoid函数进行比较。使用更一般的高斯分布不会改变模型，因为这相当于线性系数的重新缩放。许多数值包提供了一个密切相关的函数的评估：

被称为erf 函数或误差函数(不要与机器学习模型的误差函数混淆)。它与probit函数有关：

基于probit激活函数的广义线性模型称为probit回归。

我们可以使用最大似然确定这个模型的参数。在实际应用中，probit回归的结果与logistic回归的结果相似。

可能发生在实际应用的一个问题是异常值，可由如输入向量的测量误差或目标值的错误标记引起。因为这样的点可能在离理想决策边界的错误一侧很远，它们会严重地扭曲分类器。逻辑和概率单位回归模型在这方面表现不同因为当时，logistic sigmoid函数的尾部近似于渐近衰减，而对于probit激活函数来说，它们像一样衰减，因此probit模型对异常值更加敏感。

但logistic模型和probit模型都假设数据被正确标记。标签错误的影响是很容易融入一个概率模型通过引入目标值在错值浮动的概率，导致数据点的目标值分布形式为：

式中是输入向量的激活函数。可能提前设置，或者它可能被视为可以从数据中推断的超参数。

7 规范的链接函数

对于含有高斯噪声分布的线性回归模型，其负对数似然值对应的误差函数为式12。如果我们从数据点对误差函数的贡献对参数向量求导，它的形式是误差乘以特征向量，其中。

同样，对于logistic sigmoid激活函数与交叉熵误差函数(式90)的组合，以及softmax激活函数与多类交叉熵误差函数(式108)的组合，我们再次得到了同样简单的形式。现在表明，这是一个一般的结果，假设条件分布的目标变量来自指数族，以及相应激活函数的选择称为规范链接函数(canonical link function)。

我们再次使用指数族分布的限制形式式84。这里将指数族分布的假设应用于目标变量，而不是应用于输入向量。因此，考虑了目标变量的条件分布的形式：

使用与推导结果式32相同的论证，看到的条件均值用表示是：

因此，和必须有关联，用来表示这种关系。

我们定义了一个广义线性模型(generalized linear model)，其中是输入(或特征)变量的线性组合的非线性函数，因此：

式

式中在机器学习中叫激活函数，在统计中叫链接函数。

现在考虑这个模型的对数似然函数，它是的函数：

式中我们假设所有的观测都有一个共同的尺度参数(例如对应于高斯分布的噪声方差)，所以独立于。对数似然对模型参数的导数是：

其中，对使用和结果式119。我们现在看到，如果为所给的链接函数选择一个特殊的形式，就会有一个相当大的简化：

式

这使，因此。也因为，，因此。在这种情况下，误差函数的梯度减小为：

对于高斯函数，而对于logistic模型。