一、题目链接
http://codeforces.com/gym/101490
二、题面


三、题意
给你一个图,n个点,m条边,一个x,从顶点1走到顶点n。假设从顶点1走到顶点n的最短路为d,x代表你可以选择的路径的长度范围:[d, d * (1 + x%)]。让你求出在所有长度在此区间内的路径,路径上最大的边的最小值。如图所示:
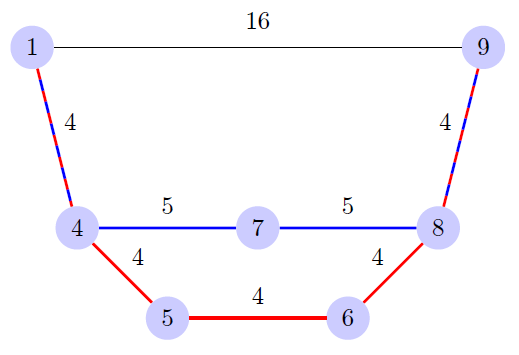
从顶点1到顶点9的最短距离为16。所以,可选的路径范围是:[16, 18.4]。可以发现,1->4->7->8->9这条路径的长度为18,是在此区间内的,而且这条路径上的边最大值为5。而另一条有效路径是1->9,边最大值是16。所以,答案是5。
四、思路
先跑一遍最短路算法,得到从顶点1到顶点n的最短路径。然后,二分最大边权,把大于枚举值mid的边全部删掉,再跑最短路,如果从1到n的最短路在[d, d * (1 + x%)]范围内,说明枚举的mid是有效的。最后输出枚举的最小的最大值即可。
删边怎么删呢?千万别用set或者vector之类的容器去模拟删除,这样复杂度会大很多。快速的方法是:使用两个图,一个是原图,另一个是二分最大边权的图,每次枚举一个mid时,都用原图来筛选,把大于mid的边直接过滤掉就OK了。
为什么这样是正确的呢?因为答案是满足单调性的。(现在我只能这么写。有些感觉上的东西实在是表达不出来呀。)
五、源代码
#include<bits/stdc++.h> using namespace std; typedef long long LL; typedef pair<int, LL> PLL;//first:邻接点,second:和邻接点之间的边权。 const int MAXN = 1e4 + 10; vector<PLL> g[2][MAXN]; int n, m, x; double minl, maxl; typedef pair<LL, int> P;//跑dijstra算法必备的。 LL d[MAXN];LL djst(int s, int which) {priority_queue<P, vector<P>, greater<P> > que;memset(d, 0x3f, sizeof(d));d[s] = 0;que.push(P(0, s));while(!que.empty()) {P p = que.top();que.pop();int v = p.second;if(d[v] < p.first)continue;for(int i = 0, sz = g[which][v].size(); i < sz; ++i) {PLL pll = g[which][v][i];if(d[pll.first] > d[v] + pll.second) {d[pll.first] = d[v] + pll.second;que.push(P(d[pll.first], pll.first));}}}return d[n]; }bool test(LL mid){for(int i = 0;i < MAXN;++i)g[1][i].clear();for(int i = 1;i <= n;++i){for(int j = 0, sz = g[0][i].size();j < sz;++j){PLL pll = g[0][i][j];if(pll.second <= mid)g[1][i].push_back(pll);}}LL dis = djst(1, 1);double ddis = (double)dis;if(ddis > minl && ddis < maxl)return true;if(fabs(ddis - minl) < 1e-10 || fabs(ddis - maxl) < 1e-10)return true;return false; }int main() { #ifndef ONLINE_JUDGEfreopen("Einput.txt", "r", stdin); #endif // ONLINE_JUDGEint a, b;LL c;while(~scanf("%d%d%d", &n, &m, &x)) {for(int i = 0; i < MAXN; ++i)g[0][i].clear();for(int i = 1; i <= m; ++i) {scanf("%d%d%lld", &a, &b, &c);g[0][a].push_back(make_pair(b, c));g[0][b].push_back(make_pair(a, c));}minl = (double)djst(1, 0);maxl = minl * (1.0 + x * 1.0 / 100.0);LL low = -1, high = 1LL << 60, mid;while(low < high - 1){mid = (low + high) / 2;if(test(mid))high = mid;else low = mid;}printf("%lld\n", high);}return 0; }
经验:long long类型的数值做数组下标也是没问题的。这样,在需要使用long long数据类型的题目中,通通使用long long数据类型,包括for循环,这样可以省去各种麻烦的类型转换操作。尤其是使用C/C++语言,编译器没有自动类型转换的情况下。
