当前位置：首页 > news >正文

免费的网站认证/软文范例大全500字

news 2025/6/30 14:40:16

免费的网站认证,软文范例大全500字,web页面显示wordpress,局域网网站原文 1 原理简介微分方程可以写成2部分： 第一部分满足初始和边界条件并包含不可调节参数第二部分不会影响第一部分，这部分涉及前馈神经网络，包含可调节参数(权重)。因此在构建微分方程的函数时，要满足上述两个条件&#xff…

原文

1 原理简介

微分方程可以写成2部分：

第一部分满足初始和边界条件并包含不可调节参数
第二部分不会影响第一部分，这部分涉及前馈神经网络，包含可调节参数(权重)。

因此在构建微分方程的函数时，要满足上述两个条件，今天就来简单看下。

假设存在以下微分方程：

上述微分方程f对应着一个函数u(t)，同时满足初始条件u(0)=u_0，为此可以令：

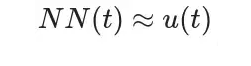
则NN(t)的导数为：

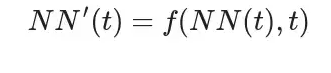
根据以上等式，NN(t)的导数近似于：

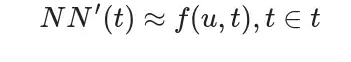
可以把上式转换成损失函数：

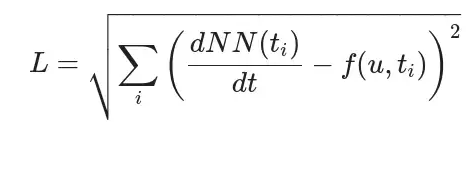
简而言之，就是已知微分函数，然后用神经网络去拟合该微分函数的原函数，然后用微分公式作为损失函数去逼近原微分函数。

微分公式：

此外，还需要将初始条件考虑进去：

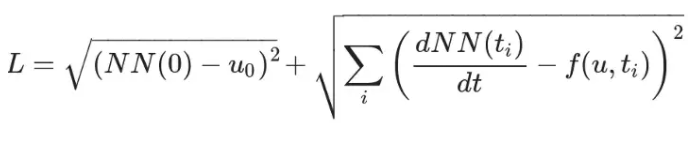
上述并不是一个好的方法，损失项越多会影响稳定性。为此会定义一个新函数，该函数要满足初始条件同时是t的函数：

则损失函数为：

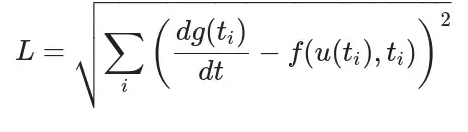
注意，神经微分网络目前主要是去近似一些简单的微分函数，复杂的比较消耗时间以及需要高算力。

2 实践

假设存在下述微分函数和网络：

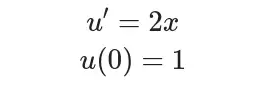
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as npnp.random.seed(123)
tf.random.set_seed(123)"""微分初始条件以及相应参数定义"""
f0 = 1 # 初始条件 u(0)=1# 用于神经网络求导,无限小的小数
inf_s = np.sqrt(np.finfo(np.float32).eps) learning_rate = 0.01
training_steps = 500
batch_size = 100
display_step = training_steps/10"""神经网络参数定义"""
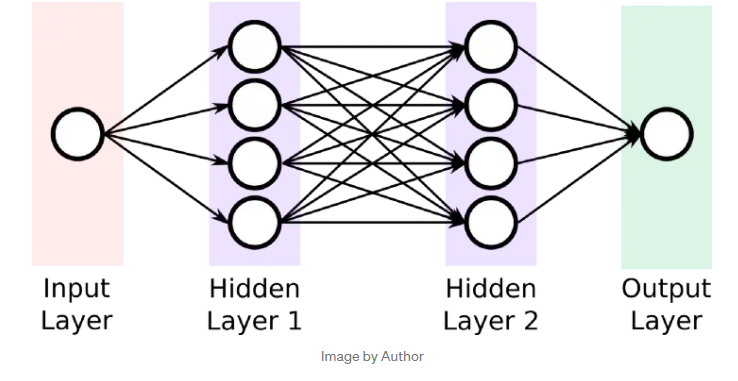
n_input = 1     # 输入维度
n_hidden_1 = 32 # 第一层输出维度
n_hidden_2 = 32 # 第二层输出维度
n_output = 1    # 最后一层输出维度
weights = {
'h1': tf.Variable(tf.random.normal([n_input, n_hidden_1])),
'h2': tf.Variable(tf.random.normal([n_hidden_1, n_hidden_2])),
'out': tf.Variable(tf.random.normal([n_hidden_2, n_output]))
}
biases = {
'b1': tf.Variable(tf.random.normal([n_hidden_1])),
'b2': tf.Variable(tf.random.normal([n_hidden_2])),
'out': tf.Variable(tf.random.normal([n_output]))
}
"""优化器"""
optimizer = tf.optimizers.SGD(learning_rate)"""定义模型和损失函数"""
"""多层感知机"""
def multilayer_perceptron(x):x = np.array([[[x]]],  dtype='float32')layer_1 = tf.add(tf.matmul(x, weights['h1']), biases['b1'])layer_1 = tf.nn.sigmoid(layer_1)layer_2 = tf.add(tf.matmul(layer_1, weights['h2']), biases['b2'])layer_2 = tf.nn.sigmoid(layer_2)output = tf.matmul(layer_2, weights['out']) + biases['out']return output"""近似原函数"""
def g(x):return x * multilayer_perceptron(x) + f0"""微分函数"""
def f(x):return 2*x"""定义损失函数逼近导数"""
def custom_loss():summation = []# 注意这里，没有定义数据，根据函数中t的范围选取了10个点进行计算for x in np.linspace(0,1,10):dNN = (g(x+inf_s)-g(x))/inf_ssummation.append((dNN - f(x))**2)return tf.reduce_mean(tf.abs(summation))"""训练函数"""
def train_step():with tf.GradientTape() as tape:loss = custom_loss()trainable_variables=list(weights.values())+list(biases.values())gradients = tape.gradient(loss, trainable_variables)optimizer.apply_gradients(zip(gradients, trainable_variables))"""训练模型"""
for i in range(training_steps):train_step()if i % display_step == 0:print("loss: %f " % (custom_loss()))"""绘图"""
from matplotlib.pyplot import figure
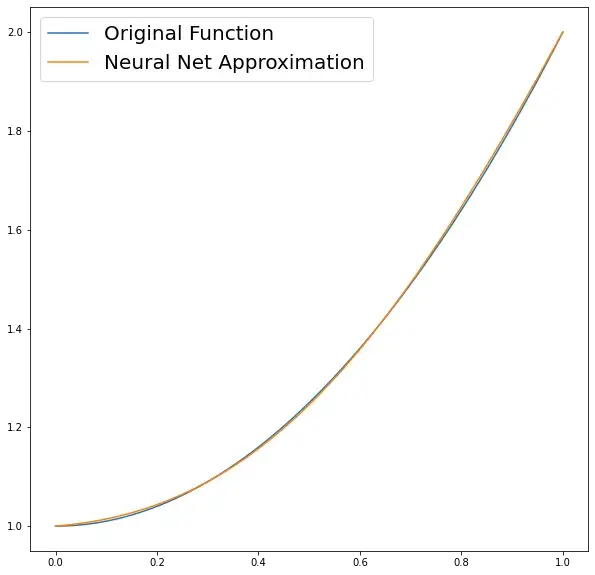
figure(figsize=(10,10))# True Solution (found analitically)
def true_solution(x):return x**2 + 1X = np.linspace(0, 1, 100)
result = []
for i in X:result.append(g(i).numpy()[0][0][0])S = true_solution(X)
plt.plot(X, S, label="Original Function")
plt.plot(X, result, label="Neural Net Approximation")
plt.legend(loc=2, prop={'size': 20})
plt.show()