第四章 多变量线性回归

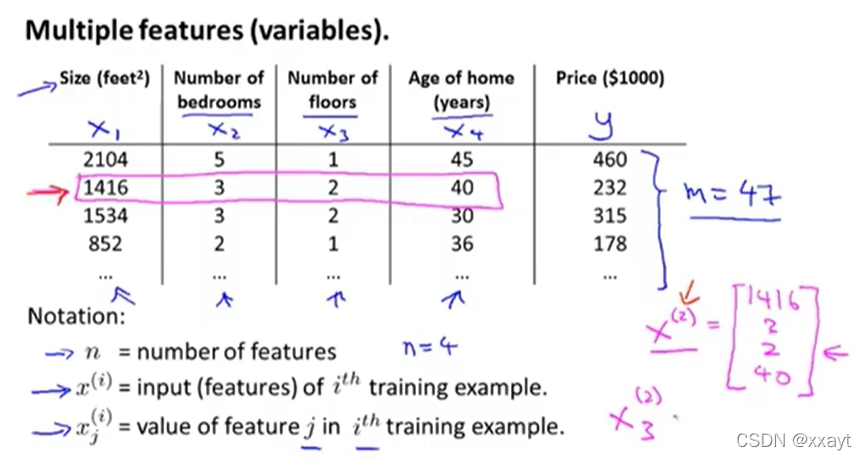
4.1 多变量 Multiple features

• 标记 Notation：
  • $n$：特征数量（变量数量）
  • $m$ ：样本数量
  • $x^{(i)}$ ：索引样本（一个 $n$ 维变量）
  • $x_j^{(i)}$：第 $i$ 个样本的第 $j$ 个特征量的值

• 函数变化：$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n$.
  • 内积 inner product 表示：设 $x_0=1$，则 $h_{\theta }(x)={\theta }^T\cdot x=\left[\begin{array}{c}{\theta }_0,{\theta }_1,{\theta }_2,...,{\theta }_n\end{array}\right]\cdot \left[\begin{array}{c}{x}_0\\ x_1\\ x_2\\ ...\\ x_n\end{array}\right]$，记为多元线性回归 Multivariate linear regression。

4.2 多元梯度下降法

Hypothesis：$h_{\theta }(x)={\theta }^{T}x={\theta }_0{x}_0+{\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n$

Parmeters：$\hat{\theta }={\theta }_0,{\theta }_1,...,{\theta }_n$

Cost function：$J({\theta }_0,{\theta }_1,...,{\theta }_n)=J(\hat{\theta })=\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }(x^{(i)})-y^{(i)}\right)}^2$

• 梯度下降法 Gradient Descent：当 $n\ge 1$ 时
  $$Repeat\left\{{\theta }_j:={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m\left(h_{\theta }(x^{(i)})-y^{(i)}\right)x_j^{(i)}\right\}j=0,1,...,n$$
  

• 特征缩放 Feature Scaling：

  • 目的：使得特征量范围相近，减少迭代次数，增加下降速度
  • 方法：使得每个特征量在 $[-1,1]$ 的范围内。（若大于 $[-3,3]$ 或小于 $[-\frac{1}{3},\frac{1}{3}]$ 时就需要除以最大值进行调整）
  

  • 均值归一化 Mean Normalization：先用 $x_i-{\mu }_i$ 代替 $x_i$ 来使平均值约为 $0$

    近似即可

    $$x_i⟵\frac{x-{\mu }_i}{s_i}=\frac{x-{\mu }_i}{\max -\min }$$

• 学习率 Learning Rate：$\alpha$

  Gradient descent：${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J(\theta )$

  • 自动收敛测试：$J({\theta }_k)-J({\theta }_{k+1})\le \epsilon$

  • 代价函数随迭代步数增加的变化曲线：

    1. 可判断梯度下降法是否已收敛（当曲线几乎平坦时）
       

    2. 可判断梯度下降法是否正常工作（保证曲线单调下降）。若曲线上升，说明需用更小的学习率

       

  • 总结：$\alpha$ 太小，导致收敛过慢。$\alpha$ 太大，可能导致代价函数 $J(\theta )$ 不下降或不收敛。

  • $\alpha$ 选择方法：三倍一取，即 $\alpha =0.001,0.003,0.01,0.03,0.1,0.3$

4.3 特征和多项式回归

• 选择特征 Choose Features：当预测房价时，已知临街宽度 frontage 与纵深宽度 depth 得到回归方程
  $$h_{\theta }(x)={\theta }_0+{\theta }_1\times \text{frontage}+{\theta }_2\times \text{depth}$$但是更好的回归方程应该为
  $$\begin{gathered} \text{area}=\text{frontage}\times \text{depth} \\ {h}_{\theta }(x)={\theta }_0+{\theta }_1\times \text{area} \end{gathered}$$即 area 为新的更合适的特征(变量)。

• 多项式回归 Polynomial Regression：利用线性回归拟合复杂函数（例：非线性函数）

  • 选择特征为初始特征的函数，代入回归方程中
  • 应用特征缩放：使不同函数的特征值可比较
    

4.4 正规方程

正规方程：一种求线性回归的代价函数 $J(\theta )$ 取最小值时的 $\theta$ 的解析解法，无需运行迭代方程

• 微积分求(偏)导，使(偏)导数为零，解方程。

  缺点：计算量太大

• 正规方程法 Normal equation：

  • 例题：样本数量 $m=4$ 的数据集

    方法：加入 $x_0$，使其均置为 $1$。建立设计矩阵 Design Matrix $X_{m\times (n+1)}$ 和 $y_m$，则
    $$\theta =(X^{T}x{)}^{-1}{X}^{T}y$$为函数取最小值时的解 $\theta$

    Matlab 代码：

    pinv(X' * X) * X' * y  # Octave
    

  • 优点：

    1. 不需要根据迭代次数最少尝试不同的学习率 $\alpha$
    2. 不需要迭代

  • 缺点：由于 $(X^{T}X{)}^{-1}$ 是 $n\times n$ 矩阵，计算逆矩阵复杂度为 $O(n^3)$，若 $n$ 很大时，计算将会很慢。一般 $n<10000$ 时可以用正规方程法。
    

• 正规方程的不可逆性：当 $(X^{T}X{)}^{-1}$ 为奇异 Singular 或退化矩阵 Degenerate Matrices 时

  Octave 内使用 pinv() 函数（即伪逆函数 pseudo-inverse），可无视是否可逆

  • 主要原因：
    1. 存在冗余变量 Redundant Features：即线性相关
       方法：删除相关变量
    2. 变量太多(数据太少)：即 $m\le n$
       方法：删除变量或使用正则化 Regularization
       即线性相关