前言：

关于BP以及链式法则的意义不用多说，cs231n也专门提供了两个PDF，非常有用，建议看一下。
一个是derivations BP and vectorization，讲述了不同维度输入输出之间如何求导。
Derivatives, Backpropagation, and Vectorization
另一个是 BP for a linear layer，解决了一半全连接层的BP问题，基本可以解决所有神经网络的BP问题。
Backpropagation for a Linear Layer
这两个链接不翻墙也可以下。

Derivatives, Backpropagation, and Vectorization

这个前半部分介绍了不同形状的input output如何求导，后半部分和下一篇基本重复。
求导就是y的每个元素对x的每个元素求导。

1. y,x都是标量。显然$\frac{\partial y}{\partial x}$也是一个标量。
2. y是标量，x是一维向量。$\frac{\partial y}{\partial x}$也是一个向量，每个元素是y对x的每个维度的偏导。
3. y,x都是一维向量。$\frac{\partial y}{\partial x}$是一个矩阵$W$，$W_{i,j}$是$\frac{\partial y_i}{\partial x_j}$
4. y,x都是高维矩阵。$\frac{\partial y}{\partial x}$就是一个高维矩阵，形状为yx叉乘的维度。(这里他提出了一个广义矩阵的概念，就是将y,x的形状当成一个标量一样运算，但是实际上没有什么意义，后面可以看到在BP里面都是一个标量L对矩阵BP，高维矩阵作为中间过程有办法跳过。)

Backpropagation for a Linear Layer

这就是重点了。
重要性质
$\frac{\partial L}{\partial x}$,$\frac{\partial L}{\partial W}$,$\frac{\partial L}{\partial b}$是标量对一维向量 or 矩阵求导，不管中间套娃多少层其形状肯定和x，W，b一样。

如标题所言，linear layer。作者给出了下面一个可以代表所有情况的例子。

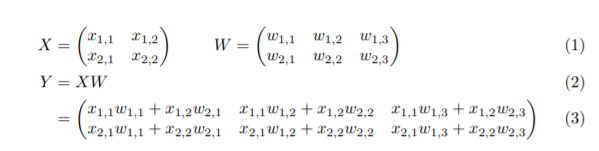
其中上游导数$\frac{\partial L}{\partial Y}$认为是已知的，是下面这样;

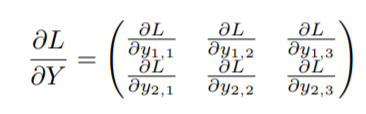
如果直接链式法则的话：
$\frac{\partial L}{\partial Y}$是一个（2,3）的矩阵。
$\frac{\partial Y}{\partial X}$是一个（2,3）$\times$（2,2）的四维矩阵。显然是难以表现。
但是仔细想想，最终的$\frac{\partial L}{\partial X}$是一个（2,2）的矩阵。四维矩阵只在中间过程中出现。所以作者就像能不能对矩阵中的单个元素进行分析，得到一些规律性的东西规避了高维矩阵。（这个思想非常有亮点，宏观微观的接合）

单个元素分析：
分析$\frac{\partial Y}{\partial X_{1,1}}$。
可以认为是$\sum _{forally}\frac{\partial L}{\partial Y}\frac{\partial Y}{\partial X_{1,1}}$。
具体展开带入：

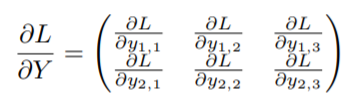
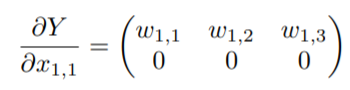
$$\frac{\partial L}{\partial X_{1,1}}=\frac{\partial L}{\partial Y_{1,1}}\frac{\partial Y_{1,1}}{\partial X_{1,1}}+\frac{\partial L}{\partial Y_{1,2}}\frac{\partial Y_{1,2}}{\partial X_{1,1}}+......+\frac{\partial L}{\partial Y_{2,3}}\frac{\partial Y_{2,3}}{\partial X_{1,1}}$$
其中后三项都是零，所以：
$$\frac{\partial L}{\partial X_{1,1}}=\frac{\partial L}{\partial Y_{1,1}}{w}_{1,1}+\frac{\partial L}{\partial Y_{1,2}}{w}_{1,2}+\frac{\partial L}{\partial Y_{1,3}}{w}_{1,3}$$
然后整合一下，通过目测法：

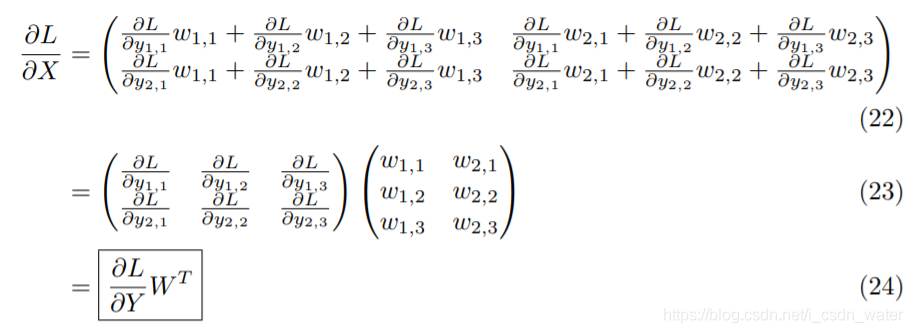
作者算这个$\frac{\partial L}{\partial X_{1,1}}$最后还是变成矩阵了，可能更加有道理，但是我的更好理解，至少对我来说。

结论

这个两个结论是最重要的，后面直接用不需要再依照元素分析了。
$$ifY=XW:$$
$$\frac{\partial L}{\partial W}=X^T\frac{\partial L}{\partial Y}$$
$$\frac{\partial L}{\partial W}=\frac{\partial L}{\partial Y}{W}^T$$