如何用rp做网站/sem推广软件哪家好

今晚的数学基础主要是概率论和一些常用的分布复习。关于概率论这块，我之前也整理过一点内容，可以点击：

今晚也简单对内容进行相对系统地复习呗～

我们最先接触概率论这块领域应该都是从抛硬币和掷骰子开始的吧，慢慢地接触集合、独立事件、相关事件、条件概率、贝叶斯公式等等，概率论与数理统计在大学还是一门比较广泛的课程，大多数的理工科专业都是会学习，相信大家对这块也是有了解，不过可能因为太久没有，有可能会有所忘记，下面就做一下简单的回顾。

1、集合运算 Set Operation

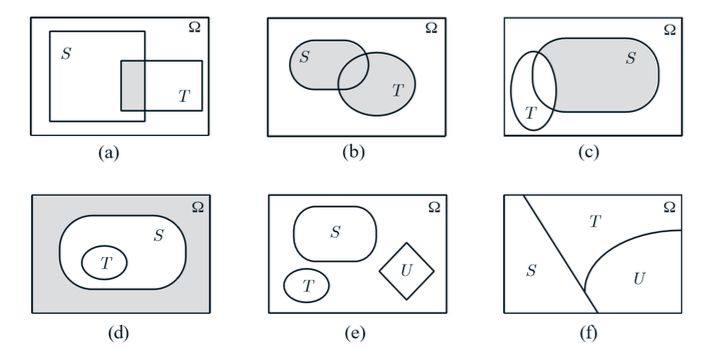
这里涉及到交集、并集、补集、全集等的概念，下面是一些例子，分别是：

(a) 阴影部分表示S和T的交集

(b) 阴影部分表示S和T的并集

(c) 阴影部分表示S独立与T的部分

(d) 阴影部分表示S和T的补集，其中T属于S

(e) 表示S和T和U相互独立，但并集小于全集

(f) 表示S和T和U相互独立，但并集就是全集

2、条件概率 Conditional Probability

条件概率十分常见，下面是关于它的一些定义。

当然，为了辅助理解，下面还有一个例子。

假设，你的邻居告诉你，他有2个小孩。

下面有2个假设，问：

1）他告诉你，其中有一个小孩是男孩，问另一个是女孩的概率？

2）如果你有天看到邻居门前有一个男孩在玩耍，问另一个是女孩的概率？

答案是2/3 和 1/2

3、全概率定理 Total Probability Theorem

下面是它的定义：

4、协方差 Covariance

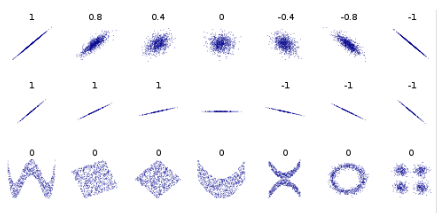
在概率论和统计学中，协方差用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。

期望值分别为E[X]与E[Y]的两个实随机变量X与Y之间的协方差Cov(X,Y)定义为：

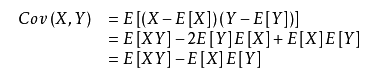
5、连续型概率密度函数 Continuous PDF

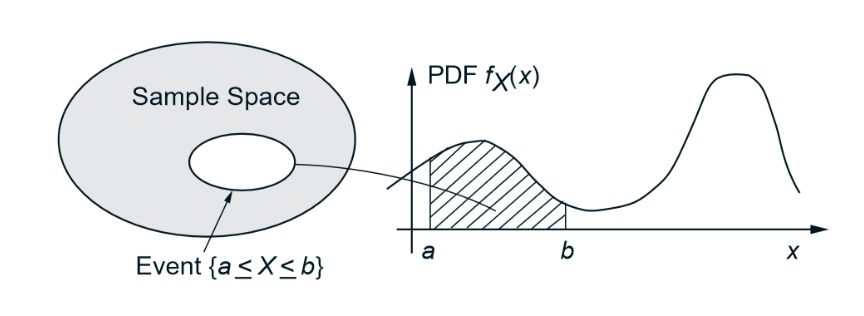
PDF，全称为robability density function，即概率密度函数，是一个描述这个随机变量的输出值，在某个确定的取值点附近的可能性的函数。而随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分。

图中阴影部分的面积为事件发生在a-b之间的概率大小。

6、伯努利分布 Bernoulli Distribution

又名两点分布或者0-1分布，是一个离散型概率分布，若伯努利试验成功，则伯努利随机变量取值为1。若伯努利试验失败，则伯努利随机变量取值为0。记其成功概率为p，则失败概率为q = 1 − p

7、二项分布 Binomial Distribution

二项分布就是重复n次独立的伯努利试验。在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变，则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布服从0-1分布。

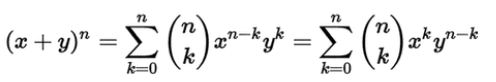
Pascal's triangle（中国叫杨辉三角），为二项分布展开式的系数。

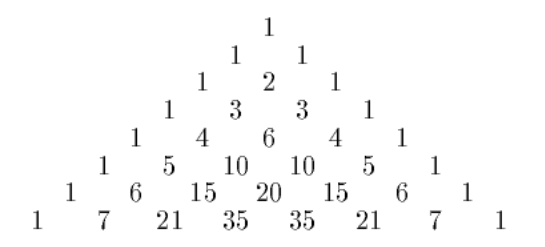
8、多项分布 Multinomial Distribution

多项式分布（Multinomial Distribution）是二项式分布的推广。

某随机实验如果有k个可能结局A1、A2、…、Ak，分别将他们的出现次数记为随机变量X1、X2、…、Xk，它们的概率分布分别是p1，p2，…，pk，那么在n次采样的总结果中，A1出现n1次、A2出现n2次、…、Ak出现nk次的这种事件的出现概率P有下面公式：

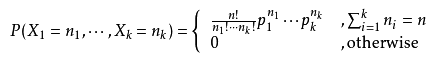
用另一种形式写为：

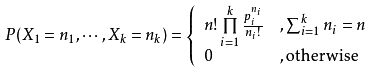
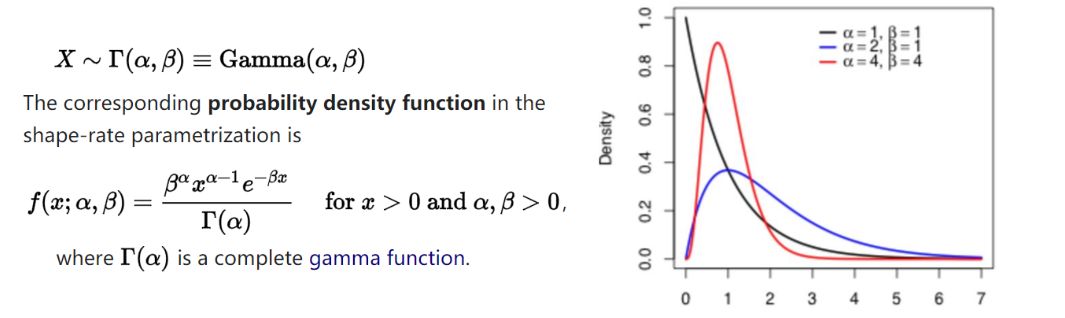
9、伽马分布 Gamma Distribution

伽玛分布（Gamma Distribution）是统计学的一种连续概率函数，是概率统计中一种非常重要的分布。“指数分布”和“χ2分布”都是伽马分布的特例。

Gamma分布中的参数α称为形状参数（shape parameter），β称为尺度参数（scale parameter）。

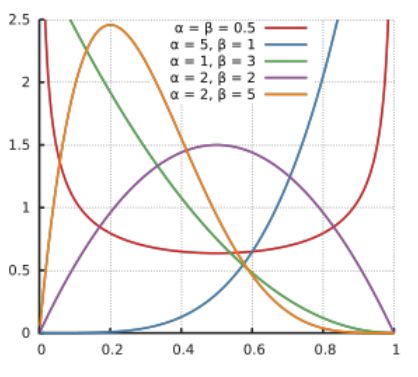
10、贝塔分布 Beta Distribution

贝塔分布（Beta Distribution) 是一个作为伯努利分布和二项式分布的共轭先验分布的密度函数。是指一组定义在  区间的连续概率分布，有两个参数  

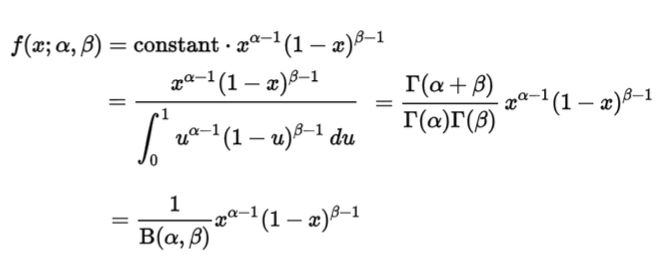
11、泊松分布 Poisson Distribution

泊松分布我们是经常见到的，其概率函数为：

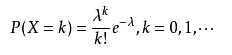
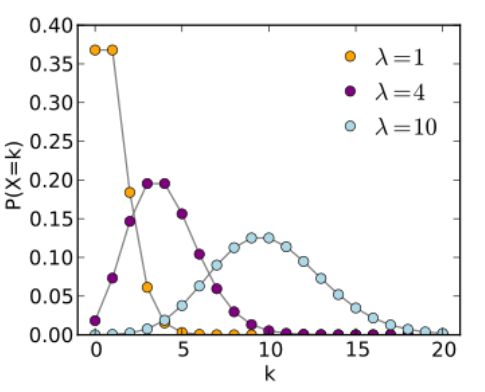
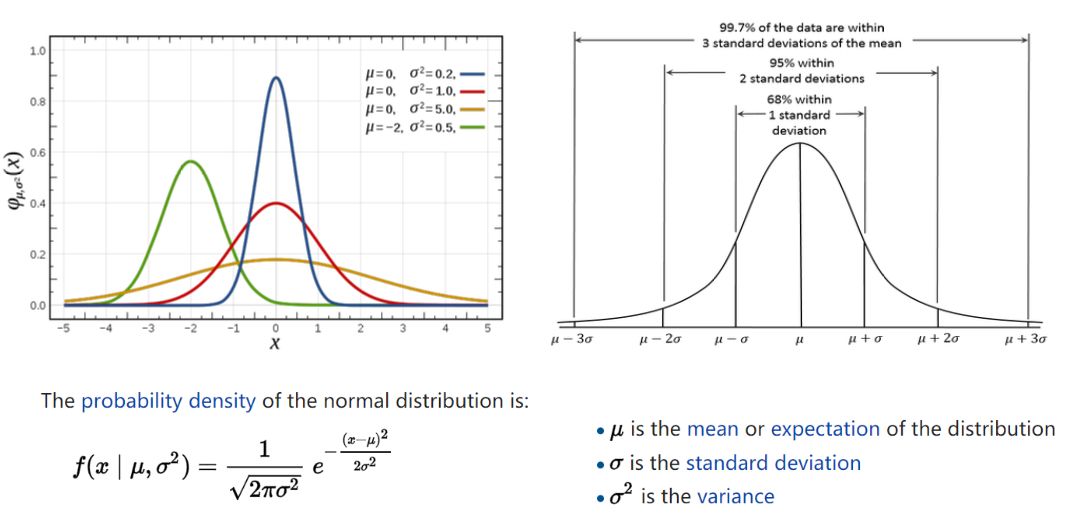
12、高斯分布 Gaussian (Normal) Distribution

即正态分布，最为常见了。

备注：内容来自于小象学院的《机器学习全新升级版》的课程内容，主讲人为秦曾昌老师。

—End—