c 网站开发案例详解百度云/爱链工具
高阶函数英文叫 Higher-order function,它的定义很简单,就是至少满足下列一个条件的函数:
- 接受一个或多个函数作为输入
- 输出一个函数
一、高阶函数实现AOP
AOP(面向切面编程)的主要作用就是把一些和核心业务逻辑模块无关的功能抽取出来,然后再通过“动态织入”的方式掺到业务模块种。这些功能一般包括日志统计,安全控制,异常处理等。AOP是Java Spring架构的核心。下面我们就来探索一下再Javascript种如何实现AOP
在JavaScript种实现AOP,都是指把一个函数“动态织入”到另外一个函数中,具体实现的技术有很多,我们使用Function.prototype来做到这一点。代码如下
/**
* 织入执行前函数
* @param {*} fn
*/
Function.prototype.aopBefore = function(fn){console.log(this)// 第一步:保存原函数的引用const _this = this// 第四步:返回包括原函数和新函数的“代理”函数return function() {// 第二步:执行新函数,修正thisfn.apply(this, arguments)// 第三步 执行原函数return _this.apply(this, arguments)}
}
/**
* 织入执行后函数
* @param {*} fn
*/
Function.prototype.aopAfter = function (fn) {const _this = thisreturn function () {let current = _this.apply(this,arguments)// 先保存原函数fn.apply(this, arguments) // 先执行新函数return current}
}
/**
* 使用函数
*/
let aopFunc = function() {console.log('aop')
}
// 注册切面
aopFunc = aopFunc.aopBefore(() => {console.log('aop before')
}).aopAfter(() => {console.log('aop after')
})
// 真正调用
aopFunc()二、currying(柯里化)
curring又称部分求值。一个curring的函数首先会接受一些参数,接受了这些参数之后,该函数并不会立即求值,而是继续返回另外一个函数,刚才传入的参数在函数形成的闭包中被保存起来。待到函数中被真正的需要求值的时候,之前传入的所有参数被一次性用于求值。
例子: 我们需要一个函数来计算一年12个月的消费,在每个月月末的时候我们都要计算消费了多少钱。正常代码如下
// 未柯里化的函数计算开销
let totalCost = 0
const cost = function(amount, mounth = '') {console.log(`第${mounth}月的花销是${amount}`)totalCost += amountconsole.log(`当前总共消费:${totalCost}`)
}
cost(1000, 1) // 第1个月的花销
cost(2000, 2) // 第2个月的花销
// ...
cost(3000, 12) // 第12个月的花销如果我们要计算一年的总消费,没必要计算12次。只需要在年底执行一次计算就行,接下来我们对这个函数进行部分柯里化的函数帮助我们理解
// 部分柯里化完的函数
const curringPartCost = (function() {// 参数列表let args = []return function (){/*** 区分计算求值的情况* 有参数的情况下进行暂存* 无参数的情况下进行计算*/if (arguments.length === 0) {let totalCost = 0args.forEach(item => {totalCost += item[0]})console.log(`共消费:${totalCost}`)return totalCost} else {// argumens并不是数组,是一个类数组对象let currentArgs = Array.from(arguments)args.push(currentArgs)console.log(`暂存${arguments[1] ? arguments[1] : '' }月,金额${arguments[0]}`)}}
})()
curringPartCost(1000,1)
curringPartCost(100,2)
curringPartCost()接下来我们编写一个通用的curring, 以及一个即将被curring的函数。代码如下
// 通用curring函数
const curring = function(fn) {let args = []return function () {if (arguments.length === 0) {console.log('curring完毕进行计算总值')return fn.apply(this, args)} else {let currentArgs = Array.from(arguments)[0]console.log(`暂存${arguments[1] ? arguments[1] : '' }月,金额${arguments[0]}`)args.push(currentArgs)// 返回正被执行的 Function 对象,也就是所指定的 Function 对象的正文,这有利于匿名函数的//递归或者保证函数的封装性return arguments.callee}}
}
// 求值函数
let costCurring = (function() {let totalCost = 0return function () {for (let i = 0; i < arguments.length; i++) {totalCost += arguments[i]}console.log(`共消费:${totalCost}`)return totalCost}
})()
// 执行curring化
costCurring = curring(costCurring)
costCurring(2000, 1)
costCurring(2000, 2)
costCurring(9000, 12)
costCurring()三、函数节流
JavaScript中的大多数函数都是用户主动触发的,一般情况下是没有性能问题,但是在一些特殊的情况下不是由用户直接控制。大量的调用容易引起性能问题。毕竟DOM操作的代价是非常昂贵的。下面将列举一些这样的场景:
window.resize事件mouse, input等事件- 上传进度
- ...
下面通过高阶函数的方式我们来实现函数节流
/**
* 节流函数
* @param {*} fn
* @param {*} interval
*/
const throttle = function (fn, interval = 500) {let timer = null, // 计时器 isFirst = true // 是否是第一次调用return function () {let args = arguments, _me = this// 首次调用直接放行if (isFirst) {fn.apply(_me, args)return isFirst = false}// 存在计时器就拦截if (timer) {return false}// 设置timertimer = setTimeout(function (){console.log(timer)window.clearTimeout(timer)timer = nullfn.apply(_me, args)}, interval)}
}
// 使用节流
window.onresize = throttle(function() {console.log('throttle')
},600)四、分时函数
节流函数为我们提供了一种限制函数被频繁调用的解决方案。下面我们将遇到另外一个问题,某些函数是用户主动调用的,但是由于一些客观的原因,这些操作会严重的影响页面性能,此时我们需要采用另外的方式去解决。
如果我们需要在短时间内在页面中插入大量的DOM节点,那显然会让浏览器吃不消。可能会引起浏览器的假死,所以我们需要进行分时函数,分批插入。
/**
* 分时函数
* @param {*创建节点需要的数据} list
* @param {*创建节点逻辑函数} fn
* @param {*每一批节点的数量} count
*/
const timeChunk = function(list, fn, count = 1){let insertList = [], // 需要临时插入的数据timer = null // 计时器const start = function(){// 对执行函数逐个进行调用for (let i = 0; i < Math.min(count, list.length); i++) {insertList = list.shift()fn(insertList)}}return function(){timer = setInterval(() => {if (list.length === 0) {return window.clearInterval(timer)}start()},200)}
}
// 分时函数测试
const arr = []
for (let i = 0; i < 94; i++) {arr.push(i)
}
const renderList = timeChunk(arr, function(data){let div =document.createElement('div')div.innerHTML = data + 1document.body.appendChild(div)
}, 20)
renderList()五、惰性加载函数
因为浏览器的差异性,我们要常常做各种各样的兼容,举一个非常简单常用的例子:在各个浏览器中都能够通用的事件绑定函数。
常见的写法是这样的:
// 常用的事件兼容
const addEvent = function(el, type, handler) {if (window.addEventListener) {return el.addEventListener(type, handler, false)}// for IEif (window.attachEvent) {return el.attachEvent(`on${type}`, handler)}
}这个函数存在一个缺点,它每次执行的时候都会去执行if条件分支。虽然开销不大,但是这明显是多余的,下面我们优化一下, 提前一下嗅探的过程:
const addEventOptimization = (function() {if (window.addEventListener) {return (el, type, handler) => {el.addEventListener(type, handler, false)}}// for IEif (window.attachEvent) {return (el, type, handler) => {el.attachEvent(`on${type}`, handler)}}
})()这样我们就可以在代码加载之前进行一次嗅探,然后返回一个函数。但是如果我们把它放在公共库中不去使用,这就有点多余了。下面我们使用惰性函数去解决这个问题:
// 惰性加载函数
let addEventLazy = function(el, type, handler) {if (window.addEventListener) {// 一旦进入分支,便在函数内部修改函数的实现addEventLazy = function(el, type, handler) {el.addEventListener(type, handler, false)}} else if (window.attachEvent) {addEventLazy = function(el, type, handler) {el.attachEvent(`on${type}`, handler)}}addEventLazy(el, type, handler)
}
addEventLazy(document.getElementById('eventLazy'), 'click', function() {console.log('lazy ')
})一旦进入分支,便在函数内部修改函数的实现,重写之后函数就是我们期望的函数,在下一次进入函数的时候就不再存在条件分支语句。
六、数组高阶函数reduce
6.1 reduce数组去重:遍历数组每一项,若值为数组则递归遍历,否则concat。
function flatten(arr) { return arr.reduce((result, item)=> {return result.concat(Array.isArray(item) ? flatten(item) : item);}, []);
}6.2 数值运算
假设有如下数组:
const arr = [1,2,3,4,5];求和:
const sum = arr.reduce((pre, cur) => pre + cur);
sum // 15求积:
const prod = arr.reduce((pre, cur) => pre * cur);
prod // 120求平均数:
const avrg = arr.reduce((pre, cur, i, a) => ( // 这里使用大括号{的话,不能省略return关键字i < a.length - 1 ? pre + cur : (pre + cur) / a.length
));
avrg // 3 如果这里的arr不是一个数值数组而是一个对象数组,每个对象包含一个值为数值类型的属性呢?我们只需要在回调函数中访问对象的对应属性并相加就可以了。需要注意的是初始值需要定义为与回调函数中使用pre参数时的默认类型相匹配,即数值类型的0, 否则可能得到意料之外的结果。
const objArr = [{name: "A",score: 80,
}, {name: "B",score: 75,
}, {name: "C",score: 90,
}];const scoreSum = objArr.reduce((pre, cur) => pre + cur.score, 0);
scoreSum // 245objArr.reduce((pre, cur) => pre + cur.score); // "[object Object]7590"也可以先对对象数组执行map函数得到数值数组,然后执行reduce求和:
const scoreSum1 = objArr.map(o => o.score).reduce((pre, cur) => pre + cur); // 2456.3 公倍数和公约数
首先明确这两个概念:对于a, b两个非零整数,a和b的最小公倍数(Least Common Multiple)是指可以被a和b整除的最小正整数;a和b的最大公约数(Greatest Common Divisor)是指能同时整除a和b的最大正整数。
一般求多个数之间的最大公约数,可以先求两个数之间的最大公约数,然后用此结果继续与下一个数求最大公约数,直到遍历所有数值;求多个数之间的最小公倍数也是相似的过程。但求两个数之间的最小公倍数,需要先确定最大公约数后,用它们的乘积除以它得到结果。
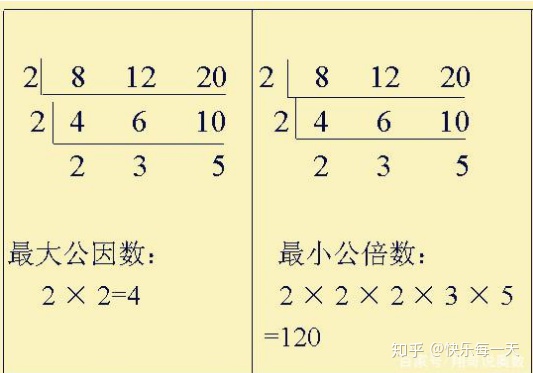
求两个数a, b的最大公约数和最小公倍数可以分别如下简单实现:
// 求两个数的最大公约数(欧几里得算法)
function maxDenom(a, b) {return b ? maxDenom(b, a % b) : a;
}// 求两个数的最小公倍数
function minMulti(a, b) {return a * b / maxDenom(a, b);
}求数组中多个数值的最大公约数和最小公倍数:
const data = [12, 15, 9, 6]const GCD = data.reduce(maxDenom)
CGD // 3const LCM = data.reduce(minMulti)
LCM // 1806.4 添加千位分隔符或四位空格
思路: 一串数字要从末尾开始向前数,每3个数字就加一个逗号,第一个数字前面一定不加逗号(有效的整数数值)。
function addSeparator(num) {const arr = [...String(num)]; // 数字转为数组const len = arr.length;return arr.reduceRight((tail, cur, i) => i === 0 || (len - i) % 3 !== 0 ? `${cur + tail}` : `,${cur + tail}`, "");
}addSeparator(12345678901) // "12,345,678,901"6.5 “大数”相加
这里的“大数”是我自己的叫法,是指数据本身位数很多,计算机的数值范围无法表示所以表示为字符串的一种“数值”。
为了保留完整结果,每一位的计算结果依然要作为字符串整合在一起,但是当前运算结果是否进位也需要传给下一个迭代,所以可以借助解构赋值,传递两个信息:[digit, tail], digit为1或0,表示后面的值相加后是否进位;tail表示已确定的各个位的计算结果。为了计算方便可以先把两个字符串倒序排列。
const s1 = '712569312664357328695151392';
const s2 = '8100824045303269669937';// 将字符串倒序并输出数值数组
function strToArrRvs(str) {return str.split("").map(x => +x).reverse();
}function addStr(a, b) {const [h, l] = (a.length > b.length ? [a, b] : [b, a]).map(strToArrRvs);// 用相对位数更多的字符串调用reducereturn h.reduce(([digit, tail], cur, idx, arr) => {const sum = cur + digit + (l[idx] || 0); // 如果遍历完成 直接输出结果, 否则输出数组用于下一次迭代return idx === arr.length - 1? sum + tail: [+(sum >= 10), sum % 10 + tail];}, [0, ""]);
}addStr('712569312664357328695151392','8100824045303269669937');
// "712577413488402631964821329"6.6 与位运算结合查找特征项
这里说的位运算包括按位与、按位或、按位异或这种二元运算符。在有一组数的情况下,因为它们满足“交换律”和“结合律”,使用reduce有时可以很方便地求解它们按位运算的结果,根据它们本身所具有的特性可能很容易地找到某些特征元素。
按位异或(对应位相异则返回1,否则返回0)a ^ b运算:
- 一个数与它自己按位异或将会得到0,因为它们每个对应位都是相同的,都会返回0,所有位都是0最后也会得到0;
- 一个数与0按位异或,则会得到这个数本身,因为对应位是0的还是0,对应位是1的还是1,相当于把这个数复制了一个。
案例:
一个整数数组中,只有一个数出现了奇数次,其他数都出现了偶数次,找到这个出现了奇数次的数。(类似变形题目如 有一个数出现了1次,其他数都出现了2次)
根据交换律和结合律,x ^ y ^ x ^ y ^ n等于(x ^ x) ^ (y ^ y) ^ n; 对所有数依次进行按位异或运算,所有出现两次的数运算结果最终还是0,而那个只出现一次的数和0按位异或得到它本身:
function findOnlyOne(arr) {return arr.reduce((pre, cur) => pre ^ cur);
}const array = [2,2,3,4,5,6,7,6,6,6,3,4,5];
findOnlyOne(array) // 7如果换成有一个数出现了5次,其他数都出现了3次呢?那就换另一种思路,如果把每个数都看作是二进制数字,它们最多不超过32位;如果能确定出现了3次的那个数在每个对应位上是0还是1,那也就确定了这个数。所以我们可以从低位到高位依次判断。
这里根据“按位与”运算的特征,两数在某位上都为1,该位返回1,否则返回0. 我们先确定一个仅在某位是1,其他位均为0的数作为标识数,然后每个数与它按位与之后再相加;假如出现了5次的数在这一位上是0,那结果一定是3的倍数(或0);否则对3取余一定为2(即5-3);
// 得到从0到31组成的数组
const iStore = (Array.from(new Array(32), (x, i) => i));
// 求解给定某特定标志数时的结果
function checkBit(flagNum, srcArr) {const bitSum = srcArr.reduce((sum, cur) => sum + (cur & flagNum), 0);return bitSum % 3 === 0 ? 0 : 1;
}// 对每一位执行求解
function checkArr(array) {const binaryStr = iStore.reduce((str, i) => checkBit(1 << i, array) + str, "");return parseInt(binaryStr, 2);
}checkArr([12,12,12,5,5,5,32,32,32,9,9,9,4,4,4,4,4]);
// 46.7 构建数组或对象
例如以下对象,我们希望改造成{name: value}的形式的对象
const info = [{name: "A",value: 4,}, {name: "B",value: 7,}, {name: "C",value: 10,}
];// 期望结果
{A: 4,B: 7,C: 10,
}
我们使用reduce,只需要一行就可以完成, 目的也会更明确:
const result = info.reduce((res, cur) => ({...res, [cur.name]: cur.value}), {});
result // {A: 4, B: 7, C: 10}构建一个新数组也是同样的道理,把空数组作为初始值,然后通过迭代向数组中添加元素,最终得到的就是想要的结果数组。
// result为上面得到的{A: 4, B: 7, C: 10}
const arrResult = Object.keys(result).reduce((accu, cur) => [...accu, {key: cur,value: result[cur]}], []);
arrResult // [{key: "A", value: 4}, {key: "B", value: 7}, {key: "C", value: 10}]6.8 数组元素去重
const sample = ["a", "b", "c", "a", "b", "d", "c"];
sample.reduce((acc, cur) => {if (!acc.includes(cur)) {acc.push(cur);}return acc;
}, []);参考:JavaScript中高阶函数的魅力 - 掘金
《Javascript设计模式》
