从零开始制作 wordpress 主题/seo每日工作

一、EKF原理
1.卡尔曼滤波原理(KF)

卡尔曼滤波是贝叶斯滤波的具体化，需要系统满足两个假设：

• 线性化假设：系统为线性系统，包含两个层面，即系统的状态转移函数为线性函数，系统的观测模型也为线性函数 。
  状态转移函数：系统从t-1时刻到t时刻不加观测量情况下状态量的变化，可以表示如下，
  $$x_t=A_t{x}_{t-1}+B_t{u}_t+{\epsilon }_t$$其中，$x_t$表示t时刻系统的状态量，若SLAM定位的对象是在二维平面上运动的轮式机器人，环境信息对应的是重要的特征点，则$$x_t=[\underset{\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{o}{\mathrm{t}}^{\prime }\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{e}}{\underbrace{x,y,\theta ,}}\underset{\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{r}\mathrm{k}1}{\underbrace{m_{1,x},m_{1,y}}},\cdots ,\underset{\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{r}\mathrm{k}\mathrm{n}}{\underbrace{m_{n,x},m_{n,y}}}{]}^T$$$u_t$表示SLAM系统里的控制量，可以理解为在t-1时刻发出的速度指令，也可以理解为在t时刻获取到的里程计信息。
  观测函数： 系统对测量值的预测，
  $$z_t=C_t{x}_t+{\delta }_t$$
• 高斯分布假设：系统的噪声服从高斯分布，主要包含三个部分，即状态转移函数噪声${\epsilon }_t$，观测模型噪声$\delta t$以及初始时刻系统状态量$x_{t_0}$均服从高斯分布，这就造成了以下三个概率，
  状态转移概率： 服从均值为0，协方差为$R_t$的高斯分布，
  $$p(x_t|x_{t-1},u_t)\sim N(0,R_t)$$观测概率： 服从均值为0，协方差为$Q_t$的高斯分布，$$p(z_t|x_t)\sim N(0,Q_t)$$初始时刻概率： 服从均值为$\mu 0$，协方差矩阵为${\Sigma }_0$的高斯分布，
  $$p(x_0)\sim N({\mu }_0,{\Sigma }_0)$$

整个KF的过程如上表所示，其中2,3两步为预测过程，表示在t时刻测量值到来之前，加入控制量$u_t$后对系统状态量的预测，而4,5,6三步为修正过程，表示综合测量信息对系统状态量预测值的修正，修正后的值即为该时刻的状态值，输出有两个方面，一个是均值${\mu }_t$，另一个是协方差${\Sigma }_t$，表示不确定度。

在看待状态估计问题中，一定不要把系统状态量看成是一个准确的值，应该将其看成一个分布，这个分布中每一个值都有可能是真实值，只不过有概率大小的区别。例如，KF里使用了高斯分布作为状态量的假设分布，而众所周知，高斯分布只需要两个量就可以描述，即均值和协方差矩阵。其中，高斯分布的均值概率最大，所以一般取均值作为系统状态量的估计值，而协方差矩阵则可以描述取均值的不确定度，在高维高斯分布里，协方差矩阵的样子为椭球形，若这个椭球越小，则代表真实值在均值附近的可能性就越大，此时不确定度就会变小，另一个角度看待这种变化就是变量被优化了。

卡尔曼滤波具体原理的推导，包括它是怎么从贝叶斯滤波根据上述假设变化的过程，可以参考Probabilistic Robotics:45-53。

2.扩展卡尔曼滤波原理(EKF)

在SLAM系统里，很难满足KF中线性化的假设，SLAM系统里的状态转移函数和观测模型均是非线性的，即，
$$\begin{array}{l}{x}_t=g(u_t,x_{t-1})+{\epsilon }_t\\ z_t=h(x_t)+{\delta }_t\end{array}$$EKF的做法是将上述的非线性函数进行泰勒展开并取前面两项近似为线性函数，即，
$$\begin{array}{l}g(u_t,x_{t-1})\approx g(u_t,{\mu }_{t-1})+g^{{}^{\prime }}(u_t,{\mu }_{t-1})(x_{t-1}-{\mu }_{t-1})\\ \\ =g(u_t,{\mu }_{t-1})+G_t(x_{t-1}-{\mu }_{t-1})\\ \\ h(x_t)\approx h({\bar{\mu }}_t)+h^{{}^{\prime }}({\bar{\mu }}_t)(x_t-{\bar{\mu }}_t)\\ \\ =h({\bar{\mu }}_t)+H_t(x_t-{\bar{\mu }}_t)\end{array}$$其中$G_t,H_t$为雅克比矩阵，$G_t=\frac{\partial g(u_t,x_{t-1})}{\partial x_{t-1}},H_t=\frac{\partial h(x_t)}{\partial x_t}$。
使用泰勒展开使得非线性函数近似线性化之后，就满足KF滤波线性化的条件了，所以后面的预测以及更新过程与KF相同。
$$\begin{array}{l}{A}_t\leftrightarrow G_t\\ C_t\leftrightarrow H_t\end{array}$$

二、SLAM里各个模型
1.机器人模型
为了方便说明，这里假设机器人为四轮移动机器人，其中前两个轮子为转向轮，后两个轮子为驱动轮，且假设其在二维的平面上运动，并且车身装有激光雷达等传感器，可对路标进行测量。

根据机器人模型的描述，可以明确机器人姿态量为$[x,y,\theta {]}^T$，并且定义输入的控制量为转向角$\gamma$和速度$V$。
这实际上相当于一个汽车的模型，后轮驱动，前轮转向，输入的转向角和速度相当于汽车的方向盘和油门。

2.运动模型
简化上图中的机器人模型：直线L表示机器人本体，前端车轮的速度归于中心点为$V$，规定转向角$\gamma$在$X_v$坐标轴上方为正（下图中的转向角为负）。

对上图表示的机器人的运动模型建立过程如下：
首先分析机器人位移$[x,y{]}^T$。将速度$V$向世界坐标系XY的两个方向分解，
$$\{\begin{array}{l}\dot{x}=V\cos (\theta +\gamma )\\ \dot{y}=V\sin (\theta +\gamma )\end{array}$$再分析机器人转角$\theta$。将速度$V$向机器人本体坐标系$X_v{Y}_v$分解，其中$V_{xv}$对转角$\theta$无影响，但$V_{xy}$可以看成是点$(x,y)$绕点E做圆周运动的线速度，则有，
$$\dot{\theta }=\frac{V_{yv}}{L}=\frac{V\sin (\gamma )}{L}$$
所以，机器人的运动模型为，
$$\{\begin{array}{l}\dot{x}=V\cos (\theta +\gamma )\\ \dot{y}=V\sin (\theta +\gamma )\\ \dot{\theta }=\frac{V\sin (\gamma )}{L}\end{array}$$由于真实情况的模型是离散的，所以对上式进行离散，
$$\{\begin{array}{l}\frac{x(k+1)-x(k)}{\Delta T}=V(k+1)\cos (\theta (k)+\gamma (k+1))\\ \\ \frac{y(k+1)-y(k)}{\Delta T}=V(k+1)\sin (\theta (k)+\gamma (k+1))\\ \\ \frac{\theta (k+1)-\theta (k)}{\Delta T}=\frac{V(k+1)\sin (\gamma (k+1))}{L}\end{array}$$进一步写成迭代形式，并且加入噪声，
$$\underset{\mathrm{k}+1时刻的状态}{\underbrace{\left[\begin{array}{l}x(k+1)\\ y(k+1)\\ \theta (k+1)\end{array}\right]}}=\underset{\mathrm{k}时刻状态}{\underbrace{\left[\begin{array}{l}x(k)\\ y(k)\\ \theta (k)\end{array}\right]}}+\underset{\mathrm{\Delta }\mathrm{T}内状态的变化量}{\underbrace{\left[\begin{array}{l}\Delta TV(k+1)\cos (\theta (k)+\gamma (k+1))\\ \Delta TV(k+1)\sin (\theta (k)+\gamma (k+1))\\ \frac{\Delta TV(k+1)\sin (\gamma (k+1))}{L}\end{array}\right]}}+\underset{\mathrm{k}+1时刻的噪声}{\underbrace{\left[\begin{array}{l}{q}_x(k+1)\\ q_y(k+1)\\ q_{\theta }(k+1)\end{array}\right]}}$$同样为了更加贴近于真实的情况，对最大的转向角和最大速度进行了限制，同时，为了方便仿真，把速度设置为某一定值，
$$\{\begin{array}{l}\left|\gamma \right|<{\gamma }_{\max }\\ \left|\dot{\gamma }\right|<{\dot{\gamma }}_{\max }\\ V=V_{const}\end{array}$$上面的两个式子即为该机器人的运动学模型。

3.观测模型
假设机器人上的传感器为激光雷达，返回的信息为路标点$i$相对于机器人的距离$z_r^i(k)$和角度$z_{\theta }^i(k)$，则根据图1，SLAM里的观测模型为，
$$h_i(x(k))+r_i(k)=\left[\begin{array}{l}\sqrt{{(x_i-x(k))}^2+{(y_i-y(k))}^2}\\ \arctan \left(\frac{y_i-y(k)}{x_i-x(k)}\right)-\theta (k)\end{array}\right]+\left[\begin{array}{l}{r}_r^i(k)\\ r_{\theta }^i(k)\end{array}\right]$$为了更加贴近实际情况，可以假设激光雷达的观测范围为车前半径为$a$的半圆内的landmark。

三、EKF在SLAM里的应用
1.明确EKF中各个模型对应于SLAM问题的含义
状态变量:如前，若地图采用的是特征地图(特征用点表示)，且机器人运动的自由度为3(在平面上运动)，则状态变量包含机器人位姿量和环境的点特征位置。
$$x_t=[\underset{\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{o}{\mathrm{t}}^{\prime }\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{e}}{\underbrace{x,y,\theta ,}}\underset{\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{r}\mathrm{k}1}{\underbrace{m_{1,x},m_{1,y}}},\cdots ,\underset{\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{r}\mathrm{k}\mathrm{n}}{\underbrace{m_{n,x},m_{n,y}}}{]}^T$$所以均值和方差为，

其中协方差矩阵的维度为$2n+3$，并且可以简写为，

状态转移函数:在SLAM里对应于机器人的运动模型。
观测模型:在SLAM里对应于机器人的观测模型。

2.EKF对SLAM系统状态量估计的大致原理描述

如上图，$R_k，R_{k+1}$表示$k，k+1$时刻机器人的位姿估计，$L_1，L_2，L_3$为机器人在$k$时刻观测到的三个特征点，在$k+1$时刻特征$L_2，L_3$又被观测到，并且同时还观测到了特征$L_4$。上图中的椭圆表示不确定度，表示真实值在椭圆范围内。那么，从$k$到$k+1$时刻，机器人根据运动模型可以估计出在$k+1$时刻的位姿$R_{k+1}$，但由于噪声的存在，误差较大，且会累计。但是由于$k+1$时刻的特征$L_2、L_3$又被观测得到，这种重复的观测会减弱这种误差的增加，从而得到更加精确的位置估计。

那么，这种利用重复观测优化系统状态量的方法就有滤波方法，当然，另外一种是图优化方法，这里只讲滤波。EKF是滤波方法的一种，它的本质其实是通过计算卡尔曼增益$K_t$来权衡模型的估计值和观测模型得到的值，以此来优化机器人位姿和环境特征点位置。而利用EKF，目的就是为了使上图的误差椭圆减小，使得机器人的状态估计更加精确（如下图）。

三、EKF_SLAM过程描述
.整个过程描述：
状态预测
数据关联
状态更新
1.状态预测：即EKF里的第2,3两步，用机器人的运动模型对机器人当前时刻的状态进行预测，即对EKF中的${\bar{\mu }}_t,{\bar{\Sigma }}_t$进行更新。

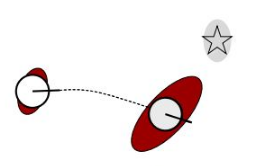
从这一幅图中可以看出，通过运动模型估计机器人位姿，它的不确定会增大，这是因为误差累计的原因。
由于仿真中的landmark是静止的，故${\bar{\mu }}_t$中的$m$和${\bar{\Sigma }}_t$中的${\Sigma }_{mm}$不需要更新，但下图中均值和协方差绿色的部分需要更新，即，

根据机器人的运动学模型更新均值，即，
$${\bar{x}}_R(t)=g_{x_R}(u_t,{\mu }_{t-1})=\left[\begin{array}{l}x(t-1)\\ y(t-1)\\ \theta (t-1)\end{array}\right]+\left[\begin{array}{l}\Delta T\cdot V(t)\cdot \cos (\theta (t-1)+\gamma (t))\\ \Delta T\cdot V(t)\cdot \sin (\theta (t-1)+\gamma (t))\\ \frac{\Delta TV(t)}{L}\sin (\gamma (t))\end{array}\right]$$
由于landmark静止，对协方差矩阵中的${\Sigma }_{mm}$不需要更新，所以，预测过程中的雅克比矩阵$G_t$可以写为，
$$G_t=\frac{\partial g(u_t,{\mu }_{t-1})}{\partial {\mu }_{t-1}}=\left[\begin{array}{lc}{G}_t^{x_R}& 0\\ 0& I\end{array}\right]$$并且其中$$\begin{array}{l}{G}_t^{x_R}=\frac{\partial g_{x_R}(u_t,x_R^{t-1})}{\partial x_R^{t-1}}=\frac{\partial }{\partial {\left[x,y,\theta \right]}^T}\left[\begin{array}{l}x+V\cdot dt\cdot \cos (\gamma +\theta )\\ y+V\cdot dt\cdot \sin (\gamma +\theta )\\ \theta +\frac{V\cdot dt\cdot \sin (\gamma )}{l}\end{array}\right]\\ \\ =\left[\begin{array}{lcc}1& 0& -V\cdot dt\cdot \sin (\gamma +\theta )\\ 0& 1& V\cdot dt\cdot \cos (\gamma +\theta )\\ 0& 0& 1\end{array}\right]\end{array}$$那么按照EKF第三步，协方差预测值如下，
$$\begin{array}{l}{\bar{\Sigma }}_t=G_t{\Sigma }_{t-1}{G}_t^T+R_t\\ \\ =\left[\begin{array}{lc}{G}_t^{x_R}& 0\\ 0& I\end{array}\right]\left[\begin{array}{lc}{\Sigma }_{x_R{x}_R}& {\Sigma }_{x_{R}m}\\ {\Sigma }_{m{x}_R}& {\Sigma }_{mm}\end{array}\right]\left[\begin{array}{lc}{(G_t^{x_R})}^T& 0\\ 0& I\end{array}\right]+R_t\\ \\ =\left[\begin{array}{lc}{G}_t^{x_R}{\Sigma }_{x_R{x}_R}{(G_t^{x_R})}^T& G_t^{x_R}{\Sigma }_{x_{R}m}\\ {(G_t^{x_R}{\Sigma }_{x_{R}m})}^T& {\Sigma }_{mm}\end{array}\right]+R_t\end{array}$$ 其中$$\begin{array}{l}{R}_t=\left[\begin{array}{lc}{R}_{x_R}& 0\\ 0& 0\end{array}\right]\\ \\ R_{x_R}=\left[\begin{array}{lcc}{\sigma }_x^2& 0& 0\\ 0& {\sigma }_y^2& 0\\ 0& 0& {\sigma }_{\theta }^2\end{array}\right]\end{array}$$这里的$R_{x_R}$是从状态变量的角度考虑的，若从控制输入量的角度考虑，即已知控制量的方差为${\sigma }_v^2,{\sigma }_{\gamma }^2$，则可以通过下式将控制量的协方差矩阵映射到机器人状态变量上来，
$$\begin{array}{l}{G}_t^u=\frac{\partial g_{x_R}(u_t,x_R^{t-1})}{\partial u_t}=\frac{\partial }{\partial u_t}\left[\begin{array}{l}x+V\cdot dt\cdot \cos (\gamma +\theta )\\ y+V\cdot dt\cdot \sin (\gamma +\theta )\\ \theta +\frac{V\cdot dt\cdot \sin (\gamma )}{l}\end{array}\right]\\ \\ =\left[\begin{array}{lc}dt\cdot \cos (\gamma +\theta )& -V\cdot dt\cdot \sin (\gamma +\theta )\\ dt\cdot \sin (\gamma +\theta )& V\cdot dt\cdot \cos (\gamma +\theta )\\ \frac{dt\cdot \sin (\gamma )}{l}& \frac{V\cdot dt\cdot \cos (\gamma )}{l}\end{array}\right]\\ \\ R_{x_R}=G_t^u\left[\begin{array}{lc}{\sigma }_v^2& 0\\ 0& {\sigma }_{\gamma }^2\end{array}\right](G_t^u{)}^T\end{array}$$
2.状态更新：即EKF里的第4,5,6三步，综合机器人的测量信息对机器人当前时刻的状态预测值进行修正，即对EKF中的${\bar{\mu }}_t,{\bar{\Sigma }}_t$进行修正，得到该时刻下的估计值。
实际过程中，第二步应该是数据关联，但为了方便说明，这里把状态更新步骤放在第二步进行说明。
根据机器人的观测模型，若第i个landmark在世界坐标系下的坐标为${\left[m_{i,x},m_{i,y}\right]}^T$，则在t时刻时，第i个landmark与机器人位置坐标的差值为${\delta }_x=m_{i,x}-x,{\delta }_y=m_{i,y}-y$，再令$q={\delta }_x^2+{\delta }_y^2$，那么根据观测模型可得，
$${\bar{z}}^i=\left(\begin{array}{l}{\bar{z}}_r^i\\ {\bar{z}}_{\theta }^i\end{array}\right)=h(\bar{\mu })=\left(\begin{array}{l}\sqrt{q}\\ \arctan 2({\delta }_x,{\delta }_y)-\theta \end{array}\right)$$其中${\bar{z}}_r^i$表示观测模型意义下landmark到机器人的欧式距离，${\bar{z}}_{\theta }^i$表示观测模型意义下landmark与机器人正方向之间的夹角。
下面计算观测模型的雅克比矩阵$H_t^i$，
首先明确输入的状态变量为：$\bar{\mu }=(x,y,\theta ,m_{i,x},m_{i,y})$
则其雅克比为，
$$\begin{array}{l}{H}_t^i=\frac{\partial h({\bar{\mu }}_t)}{\partial {\bar{\mu }}_t}=\frac{\partial }{\partial {\bar{\mu }}_t}\left(\begin{array}{l}\sqrt{{\delta }_x^2+{\delta }_y^2}\\ \arctan 2({\delta }_x,{\delta }_y)-\theta \end{array}\right)\\ \\ =\frac{1}{q}\left[\begin{array}{lcccc}-{\delta }_x\sqrt{q}& -{\delta }_y\sqrt{q}& 0& {\delta }_x\sqrt{q}& {\delta }_y\sqrt{q}\\ {\delta }_y& -{\delta }_x& -q& -{\delta }_y& {\delta }_x\end{array}\right]\end{array}$$在实际的观测过程中，landmark的数量一般不止一个，定义观测值$Z_t$如下，
Zt={z1,z2,⋯,zm}{Z_t} = \left\{ {{z_1},{z_2}, \cdots ,{z_m}} \right\}Zt​={z1​,z2​,⋯,zm​}如前定义，t时刻状态变量如下，
$${\mu }_t=[\underset{\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{o}{\mathrm{t}}^{\prime }\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{e}}{\underbrace{x,y,\theta ,}}\underset{\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{r}\mathrm{k}1}{\underbrace{m_{1,x},m_{1,y}}},\cdots ,\underset{\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{m}\mathrm{a}\mathrm{r}\mathrm{k}\mathrm{n}}{\underbrace{m_{n,x},m_{n,y}}}{]}^T$$根据观测模型和观测值的序列关系，假设观测值序列$Z_t$中的第i个landmark的观测值对应于${\mu }_t$中第j个landmark的状态值$(m_{j,x},m_{j,y})$，则可用一个数组$c$来维护观测值与状态值的对应关系，
$$\{\begin{array}{l}c[i]=ji\in [1,m],j\in [1,n]\mathrm{i}\mathrm{f}{z}_i\mathrm{c}\mathrm{a}\mathrm{n}\mathrm{b}\mathrm{e}\mathrm{f}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{n}{\mu }_t\\ c[i]=-1\mathrm{i}\mathrm{f}{z}_i\mathrm{c}\mathrm{a}\mathrm{n}\mathrm{n}\mathrm{o}\mathrm{t}\mathrm{b}\mathrm{e}\mathrm{f}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{n}{\mu }_t\end{array}$$这里需要注意的是$Z_t$中的每个landmark未必都能找到其相应的$(m_{j,x},m_{j,y})$，这种情况会发生在观测到新的landmark时(即，该landmark在之前从未被观测到过)。此时该landmark的状态值定义如下，

当然，寻找$Z_t$序列和${\mu }_t$序列对应的过程即为数据关联过程。可以用下面的这个函数表示，
$$c=associate(Z_t,{\mu }_t)$$在观察到多个landmark时，由于各个landmark之间静止且独立，所以对于第i个landmark的雅克比矩阵$H_t^i$而言，其与其他landmark的相关偏导均为零，即，

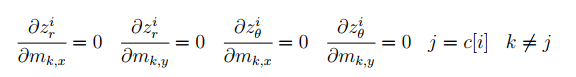
由此，此时的$H_t^i$可以写为，
$$H_t^i=\frac{1}{q}\left[\begin{array}{lcccc}-{\delta }_x\sqrt{q}& -{\delta }_y\sqrt{q}& 0& {\delta }_x\sqrt{q}& {\delta }_y\sqrt{q}\\ {\delta }_y& -{\delta }_x& -q& -{\delta }_y& {\delta }_x\end{array}\right]F_j$$并且其中$$F_j=\left[\begin{array}{lcccccc}1& 0& 0& 0\cdots 0& 0& 0& 0\cdots 0\\ 0& 1& 0& 0\cdots 0& 0& 0& 0\cdots 0\\ 0& 0& 1& 0\cdots 0& 0& 0& 0\cdots 0\\ 0& 0& 0& 0\cdots 0& 1& 0& 0\cdots 0\\ 0& 0& 0& \underset{2j-2}{\underbrace{0\cdots 0}}& 0& 1& \underset{2n-2}{\underbrace{0\cdots 0}}\end{array}\right]$$
至此，观测模型的雅克比$H_t$推导完毕，剩下来的只需要按照公式更新计算即可。

3.数据关联：在上面的状态更新阶段，需要对观测的landmark和状态向量中的landmark相匹配，这一过程就是数据关联。而数据关联的方法有很多，这里取两种讲一下。

一种是观测时数据自带唯一身份标签的。例如，在landmark上贴上二维码，使用相机读取二维码便可以确定landmark的ID。这种方法简单直接，但现实情况往往不是这样。

另外一种是观测数据不带身份标签。这时一个可行的算法是利用观测到的数据与已知的landmark间的相似度来确定，这更加符合实际情况。众所周知，一种可行的相似度度量方式是使用欧氏距离，即计算观测到的landmark坐标和所有已知的landmark间的欧式距离，求出最小距离即为对应的landmark。同时。可以通过设定阈值来判断该观测值是不是新的landmark，即若最小距离大于该阈值，则判定为新观测到的landmark。这一过程可表示如下，

但由于噪声的影响以及长度和角度量纲不一致的影响，若果简单的用欧式距离来衡量相似度很容易出错，所以这里可以用马氏距离来代替欧式距离，
$$d(x,y)=\sqrt{{(x-y)}^T{S}^{-1}(x-y)}$$其中，$x,y$服从同一分布，S表示该分布的协方差矩阵。所以，马氏距离考虑到了量纲和噪声的影响，比欧式距离更加合理。那么，与欧式距离类似，用马氏距离进行数据关联的过程如下，

当然数据关联的方法有很多，可以根据实际情况进行选取。

四、Matlab代码
有关EKF_SLAM的仿真，本文参考了EKF_SLAM算法实践一文，其文章与代码地址为https://github.com/Nrusher/EKF_SLAM。

这里放下结果，本文粗略的运行了程序，输出的机器人轨迹有三条：机器人轨迹的真实值(黑色虚线)，运动模型预测的机器人轨迹(蓝色虚线)，EKF滤波后的机器人轨迹(红色虚线)。

五、总结
EKF_SLAM是激光SLAM领域中最早期的成果之一。通过上述分析可以看出该方法的实质就是利用多次且重复的观测信息来减小机器人定位的不确定度，从而达到机器人位姿优化的目的。它主要有以下几个特点：
1.环境信息用landmark表示，地图为特征地图，稀疏且无法作为导航地图使用。
2.需要机器人的里程信息作为机器人下个时刻状态值的预测。
3.在修正误测的状态值时，需要数据关联，其精度与数据关联算法的精准度直接相关。

参考文献：
[1] SLAM笔记五——EKF-SLAM
[2] 从程序中学习EKF-SLAM（一）
[3] EKF_SLAM算法实践
[4] 概率机器人