网站制作 太原/东莞网络营销推广专业
一、模拟退火算法概述
模拟退火算法(Simulated Annealing,SA)多用以解决优化问题(寻找最优值),其退火过程可理解为:
①加温过程——设定初始温度
②等温过程——Metropolis抽样过程(Metropolis准则以一定的概率接受恶化解,使解空间覆盖更多的可能性,算法可以跳离局部最优,是收敛于全局最优的关键)
③降温过程——控制参数的下降
退火过程的能量变化目标函数
能量最低态最优解
1.SA算法步骤:
1.初始化:取初始温度T0足够大,令T= T0,任取初始解S1。(以一个解为起点,不需要在解空间初始多个解)
2.对当前温度T,重复第(3)~(6)步。
3.对当前解S1随机扰动产生一个新解S2。
4.计算S2的增量df= f(S2)- f(S1),其中f(S1)为S1的代价函数(适应度函数/目标函数)。
(模拟退火算法用以求最小值,若需要求最大值,取目标函数的负值为代价函数)
5.若增量df <0,则接受S2(较小的值)作为新的当前解,即S1 = S2,否则计算S2的接受概率exp(-df/T),即随机产生(0,1)区间上均匀分布的随机数rand,若exp(-df/T)> rand,也接受S2作为新的当前解S1=S2,否则保留当前解S1。
6.如果满足终止条件Stop,则输出当前解S1为最优解,结束程序,终止条件Stop通常取为在连续若千个Metropolis链中新解S2都没有被接受时终止算法或者是设定结束温度;否则按衰减函数衰减T(降温)后返回第(2)步。
(蓝色字体部分均由题目需求自己设计)
2.SA算法的特点
①与遗传算法、粒子群优化算法和蚁群算法等不同,模拟退火算法不属于群优化算法,不需要初始化种群操作。
②收敛速度较慢。(初始温度设置很大,终止温度设置的很小)
③温度管理(初始、终止温度的设置)、退火速度等对寻优结果均有影响。
二、TSP问题(Traveling Salesman Problem,旅行商问题)
问题描述:假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
基于模拟退火算法在Matlab中建立模型main.m:
%模拟退火算法求解旅行商问题
%%Ⅰ.清空环境变量
clear all
clc%%Ⅱ.导入城市数据(14个城市的横纵坐标数据)
X = [16.4700 96.100016.4700 94.440020.0900 92.540022.3900 93.370025.2300 97.240022.0000 96.050020.4700 97.020017.2000 96.290016.3000 97.380014.0500 98.120016.5300 97.380021.5200 95.590019.4100 97.130020.0900 92.5500];%%Ⅲ.计算距离矩阵D = Distance(X);%计算距离矩阵N = size(D,1);%城市的个数%%Ⅳ.初始化参数syms x %使用solve函数前先定义变量xT0 = 1e10;%初始温度Tend = 1e-30;%终止温度L = 2;%各温度下的迭代次数q = 0.9;%降温速率Time = ceil(double(solve(T0 *(0.9).^x == Tend)));%计算迭代的次数%Time = 132;count = 0;%迭代计数Obj = zeros(Time,1);%目标值矩阵初始化track = zeros(Time,N);%每代的最优路线矩阵初始化%%Ⅴ.随机产生一个初始路线S1 = randperm(N);%返回包含整数1:N的随机排列的向量DrawPath(S1,X)disp('初始种群中的一个随机值:')OutputPath(S1);%列出所走的路径顺序Rlength = PathLength(D,S1);disp(['总距离:',num2str(Rlength)]);%%Ⅵ.迭代优化while T0 > Tendcount = count +1;%更新迭代次数temp = zeros(L,N+1);%%%1.产生新解S2 = NewAnswer(S1);%%%2.Metropolis法则判断是否接受新解[S1,R] = Metropolis(S1,S2,D,T0);%Metropolis抽样算法%%%3.记录每次迭代过程的最优路线if count ==1 || R < Obj(count - 1)Obj(count) = R;%如果当前温度下最优路程小于上一路程,则记录当前路程elseObj(count) = Obj(count-1);%如果当前温度下最优路程大于上一路程,则记录上一路程endtrack(count,:) = S1;T0 = q*T0;%降温end%%Ⅶ.优化过程迭代图figureplot(1:count,Obj)xlabel('迭代次数')ylabel('距离')title('优化过程')%%Ⅷ.绘制最优路径图DrawPath(track(end,:),X)%%Ⅸ.输出最优解的路线和总距离disp('最优解:')S = track(end,:);p = OutputPath(S);disp(['总距离:',num2str(PathLength(D,S))]);其中,根据需要定义的函数有:
1)计算城市之间的距离矩阵的Distance.m
function D = Distance(citys)
%DISTANCE 计算两两城市之间的距离n = size(citys,1);
D = zeros(n,n);
for i=1:nfor j = i+1:nD(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));D(j,i) = D(i,j);%距离沿着对角线对称end
end
end2)绘制路径的DrawPath.m
function DrawPath(Route,citys)
%DRAWPATH 画路径函数
% Route待画路径 citys各城市坐标位置figure
plot([citys(Route,1);citys(Route(1),1)],...[citys(Route,2);citys(Route(1),2)],'o-');
grid onfor i = 1:size(citys,1)text(citys(i,1),citys(i,2),[' ' num2str(i)]);
endtext(citys(Route(1),1),citys(Route(1),2),' 起点');
text(citys(Route(end),1),citys(Route(end),2),' 终点');
end3)输出所走路径的函数OutputPath.m
function p = OutputPath(R)
%OUTPUTPATH 输出路径函数R = [R,R(1)];
N = length(R);
p = num2str(R(1));
for i =2:Np = [p,'->',num2str(R(i))];
end
disp(p)end4)计算每个个体的路径长度PathLength.m
function Length = PathLength(D,Route)
%PATHLENGTH 计算各个体Route的路径长度Length = 0;
n = size(Route,2);
for i = 1:(n-1)Length = Length + D(Route(i),Route(i+1));
end
Length = Length + D(Route(n),Route(1));
end5)产生一个新的路径解的NewAnswer.m
function S2 = NewAnswer(S1)
%NEWANSWER 加入扰动,产生一个新的路径N = length(S1);
S2 = S1;
a = round(rand(1,2)*(N-1)+1);%产生两个随机位置,用来交换
W = S2(a(1));
S2(a(1)) = S2(a(2));
S2(a(2)) = W;%得到一个新路径
end6)Metroplis抽样算法函数Metroplis.m
function [S,R] = Metropolis(S1,S2,D,T)
%Metroplis抽样算法
% 输入:S1——当前解;S2——新解;D——距离矩阵(两两城市之间的距离);T——当前温度
% 输出:S:下一个当前解;R——下一个当前解的路线距离R1 = PathLength(D,S1);%计算线路长度
N = length(S1);%得到城市的个数R2 = PathLength(D,S2);%计算线路长度
dC = R2 - R1;%计算能力之差
if dC < 0S = S2;R = R2;
elseif exp(-dC/T) >= rand %以exp(-dC/T)的概率接受新路线S = S2;R = R2;
else %不接受新路线S = S1;R = R1;
endend运行main.m得到的结果有:

随机初始化的一种路径

模拟退火算法得到的最优路径
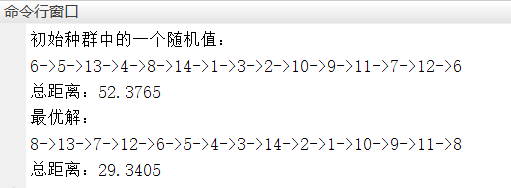
输出结果
