企业网站建设哪家好/近期的新闻消息

二进制搜索树(BSTs) 和AVL 树

基本数据结构
元素可以包含卫星数据，并且使用一个键来标识该元素。
对动态集 S 的操作：
Search(S, k)：返回带有键 k 的元素 x，或 NIL
Insert(S, x)：将元素 x 添加到 S
Delete(S, x)：从 S 中删除元素 x
最小值（S），最大值（S）：仅适用于全序集
Successor(S, x), Predecessor(S, x)：下一个或上一个元素

insert :: Ord a => a -> Tree a -> Tree a
insert a Empty = Node Empty a Empty
insert a (Node left root right)| a < root  = Node (insert a left) root right| otherwise = Node left root (insert a right)

直观地说：每个节点最多有两个子树。
我们可以递归地定义二进制树：它是一个定义为有限节点集的结构，使得树为空（无节点）或它由根节点、左子树和右子树组成
这种观点对于通过归纳证明关于树的陈述非常方便。

将列表转换为 BST（使用 foldr）

foldTree :: Ord a => [a] -> Tree a
foldTree = foldr insert Empty

树中的路径是由边链接的节点序列。 路径的长度是边的数量。
树的叶子是没有子节点的节点； 否则称为内部节点。
我们以显而易见的方式谈论兄弟姐妹、父母、祖先、后代。
树中节点的深度是从该节点到根的（简单）路径的长度。树的一个级别是一组相同深度的节点。
树中节点的高度是从该节点到叶子的最长路径的长度。一棵树的高度就是它的根的高度。
如果每个节点都是叶子或恰好有两个孩子，则二进制树是满的。
如果它已满并且所有叶子具有相同的水平，则它是完整的。

这个数据结构的定义是最好的:
data Tree a = Empty | Node (Tree a) a (Tree a)

深度和完整性
如果每个节点的两个子树大小相等，则二进制树是完整的。 定义一个决定二进制树是否完整的函数。
为了完成这个，一个典型的解决方案涉及一个高度函数：


平衡的二进制搜索树
什么是平衡树？
“如果每个子树都是平衡的，并且两个子树的高度最多相差一个，那么这棵树就是平衡的”

定义一个函数 balance :: [a] -> Tree a 将非空列表转换为平衡树。

检查二叉树是否平衡(是BST)

balanced :: (Ord a) => Tree a -> Bool
balanced Empty = True
balanced  (Node l root r)| not (balanced l) = False| not (balanced r) = False| abs ((height l) - (height r)) > 1 = False| otherwise = True

这个二叉树不平衡(不是BST)

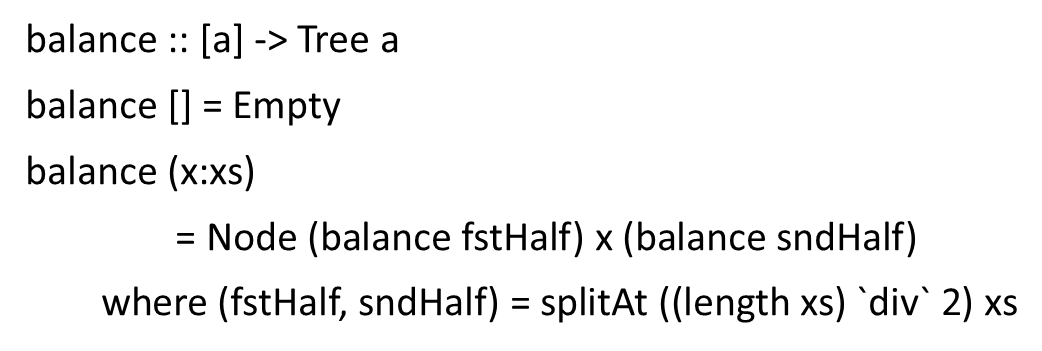
最简单的方法是将派生 Show 添加到您的类型定义中，以便获得结果

data Tree a = Empty | Node (Tree a) a (Tree a)deriving Show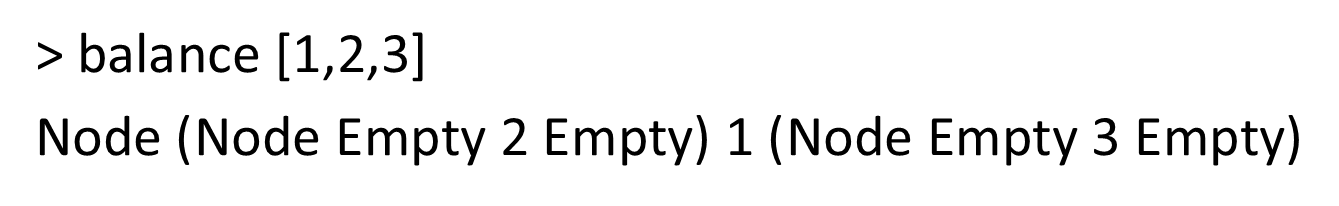

使 Tree 成为 Show 的一个实例！

结果看起来像这种格式:

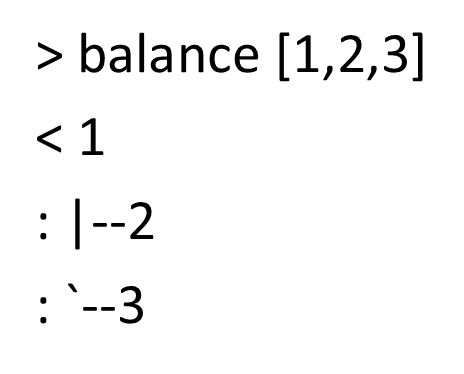
二进制搜索树(BSTs)
二进制树只有当它们是二进制搜索树时才真正有用。
提供家庭作业解决方案的平衡功能并不是很有用。
如果 y 是 x 的左子树中的一个节点，则 y.key ≤ x.key。
如果 y 是 x 的右子树中的一个节点，则 y.key ≥ x.key。
Search(S, k)：返回带有键 k 的元素 x，或 NIL
想法：与当前键比较并停止或向左或向右走。

插入一个元素

insert :: Ord a => a -> Tree a -> Tree a
insert a Empty = Node Empty a Empty
insert a (Node left root right)| a < root  = Node (insert a left) root right| otherwise = Node left root (insert a right)foldTree :: Ord a => [a] -> Tree a
foldTree = foldr insert Empty

寻找元素

contains :: Ord a => a -> Tree a -> Bool
contains a Empty = False
contains a (Node left root right)| a == root = True| a < root  = contains a left| otherwise = contains a right

平衡的 BST
所以现在 BST 搜索得到了改进，因为平均而言我只需要搜索一半。不过，我仍然可以进行完整搜索，因为我可以拥有树枝状的树
平衡的 BST 将提供更好的结果。

AVL 树
如果对于每个节点都满足以下条件，则二进制树称为 AVL 树：左子树的高度和右子树的高度最多相差 1。
我们如何确保这一点？ 在插入时平衡树：
就像在普通的二叉搜索树中一样工作。
但是树可能会变得不平衡，因此我们需要重新平衡.我们记录新元素的搜索路径，然后只要当前子树的高度增加，就可以备份搜索路径以重新平衡。

设 v 为当前节点，其右子树 x 在搜索路径上（左子树是对称的）
假设 𝑏𝑎𝑙 𝑣 ≔ 左高 - 右高
案例1：𝑏𝑎𝑙𝑣 =1。
v 的左子树在插入前高于右子树。插入 z 后，右子树的高度增加了，因此 v 处的子树现在是平衡的。v 的高度没有改变，因此完成了重新平衡。
案例2：𝑏𝑎𝑙𝑣 =0。
v 的两个子树在插入之前都是平衡的。
插入 z 后，右子树的高度增加了，因此现在𝑏𝑎𝑙𝑣 = -1。v 处的子树的高度增加了，因此我们需要继续在 v 的父级处重新平衡，以检查树上的不平衡情况。如果 v 是根，我们停止
情况 3：𝑏𝑎𝑙𝑣 = -1。
插入后，树变得不平衡：𝑏𝑎𝑙𝑣 = -2。
搜索路径包含节点 v、x、w，其子树的高度增加。我们根据 w 是 x 的右子树还是左子树来区分两种子情况。
子情况 3-1：w 是 x 的右子树。
由于“外部”问题，这棵树是不平衡的。
现在将树向左旋转：x 成为 v 的父节点，x 的左子树 B 成为 v 的子树。
子案例 3-2：w 是 x 的左子树。
由于“内部”问题，这棵树是不平衡的。
现在需要双重旋转来重新平衡树：在 x 处右旋转，然后在 v 处立即左旋转。

在最高级别

这里有新东西！
@notation… 在这里本质上意味着我们可以通过 t （对于整个树）或任何使用模式匹配的子组件来引用第二个参数。

将列表转换为 AVL 树

foldAVLTree :: Ord a => [a] -> Tree a
foldAVLTree = foldr avlInsert Empty

把它们放在一起……

balanced :: (Ord a) => Tree a -> Bool
balanced Empty = True
balanced  (Node l root r)| not (balanced l) = False| not (balanced r) = False| abs ((height l) - (height r)) > 1 = False| otherwise = Truerotate :: (Ord a) => Tree a -> Tree a
rotate Empty = Empty
rotate (Node l root r)| not (balanced l)= Node (rotate l) root r| not (balanced r)= Node l root (rotate r)| (height l) + 1 < (height r)&& (height (left r)) < (height (right r))= Node (Node l root (left r)) (value r) ((right r))| (height r) + 1 < (height l) && (height (right l)) < (height (left l))= Node ((left l)) (value l) (Node ((right l)) root r)
| (height l) + 1 < (height r)&& (height (left r)) > (height (right r))= Node (Node l root (left (left r))) (value l)(Node (right (left r)) (value r) (right r))| (height r) + 1 < (height l)&& (height (right l)) > (height (left l))= Node (Node (left l) (value l) (left (right l))) (value r)(Node (right (right l)) root r)| otherwise = Node l root rwhereleft (Node l root r) = lright (Node l root r) = rvalue (Node l root r) = root

BST 的其他特性
最小值：从根开始，向左走，直到左子树为 NIL。
最大值：从根开始，向右走，直到右子树为 NIL。
后继者：右子树中的最小值（如果存在）。
最大item/最小item

 -- Find the minimum item in a BSTminimum' :: Eq a => Tree a -> aminimum' Empty = error "Empty tree"minimum' (Node Empty root _) = rootminimum' (Node left root _) = minimum' left-- Find the maximum item in a BSTmaximum' :: Eq a => Tree a -> amaximum' Empty = error "Empty tree"maximum' (Node _ root Empty) = rootmaximum' (Node _ root right) = maximum' right-- Find the next largest item (to input value) in a BSTsuccessor :: Ord a => a -> Tree a -> asuccessor val (Node left root right)| val == root = minimum' right| val < root  = if val >= (maximum' left) then root else successor val left| otherwise = successor val right