每日一句：真正让人变好的选择过程都不会很舒服，所以人们明知道什么都不做，会比较轻松，但依旧选择追逐梦想。

---

前言

原数组: a[1], a[2], a[3], a[4], a[5], …, a[n]
前缀和: S[i] = a[1] +a[2] + a[3] + … + a[i]
前缀和能够快速的求出某一区间的和。

详细看下面的介绍。

一、一维前缀和

1.前缀和是什么？

用一个简单的列子去介绍

原数组: a[1], a[2], a[3], a[4], a[5], …, a[n]
前缀和: s[i] = a[1] + a[2] + a[3] + … + a[i]
前缀和就是用一个数组s去存数组a的前n项的和。
s[0] = 0
s[1] = a[1]
s[2] = a[1] + a[2]
s[n] = a[i] + a[2] + a[3] + …+a[n]
这样s[n]对应的就是a[1]—a[n]的和，s的每一项都这样对应，就构成了前缀和。
注：前缀和的下标一定要从1开始。

2.暴力做法

int n, m;cin >> n >> m;int sum = 0;for (int i = 1; i <= n; i++){cin >> a[i];}while (m--){int l, r;cin >> l >> r;sum = 0;for (int i = l; i <= r; i++){sum += a[i];}cout << sum << endl;}

这个就是用暴力的方法去做，也能求出区间[L,R]的和，但他的时间复杂度为O(n)那么当数据过于庞大的时候就会造成超时的情况。

暴力会超时。

3.前缀和求区间大小

如何利用前缀和去求区间大小呢？
有一个公式：s[r] - s[l - 1]。
就是这个公式，他的时间复杂度O(1)，这就要比暴力的做法快上很多了。

3.1如何构成前缀和的形式？

	for (int i = 1; i <= n; i++){s[i] = s[i - 1] + a[i];}

s[1] = s[0] + a[1];
s[2] = s[1] + a[2];
s[3] = s[2] + a[3];
s[n] = s[n - 1] + a[n]
去遍历a数组，把当前a[n]的数加上s[n-1]的数，就能得到s[n]，这个s[n]就是a[1，n]的和。

4.完整代码

#include <iostream>using namespace std;const int N = 1e6 + 10;int a[N],s[N];
//int main()//暴力做法
//{
//	int n, m;
//	cin >> n >> m;
//	int sum = 0;
//	for (int i = 1; i <= n; i++)
//	{
//		cin >> a[i];
//	}
//	while (m--)
//	{
//		int l, r;
//		cin >> l >> r;
//		sum = 0;
//		for (int i = l; i <= r; i++)
//		{
//			sum += a[i];
//		}
//		cout << sum << endl;
//	}
//	return 0;
//}
int main()//前缀和写法
{int n, m;cin >> n >> m;for (int i = 1; i <= n; i++){cin >> a[i];}for (int i = 1; i <= n; i++){s[i] = s[i - 1] + a[i];}while (m--){int l, r;cin >> l >> r;cout << s[r] - s[l - 1] << endl;}return 0;
}

例题acwing795.前缀和

二、二维前缀和

1.基本思路

二维前缀和是建立在一维前缀和的基础上实现的，唯一不同的就是，这个是二维的。

s[1][1] = s[0][1] + s[1][0] - s[0][0] + a[1][1];
s[2][2] = s[1][2] + s[2][1] - s[1][1] + a[2][2];
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
注：下标从1开始
这样理解可能有点困难，画个图就知道了。

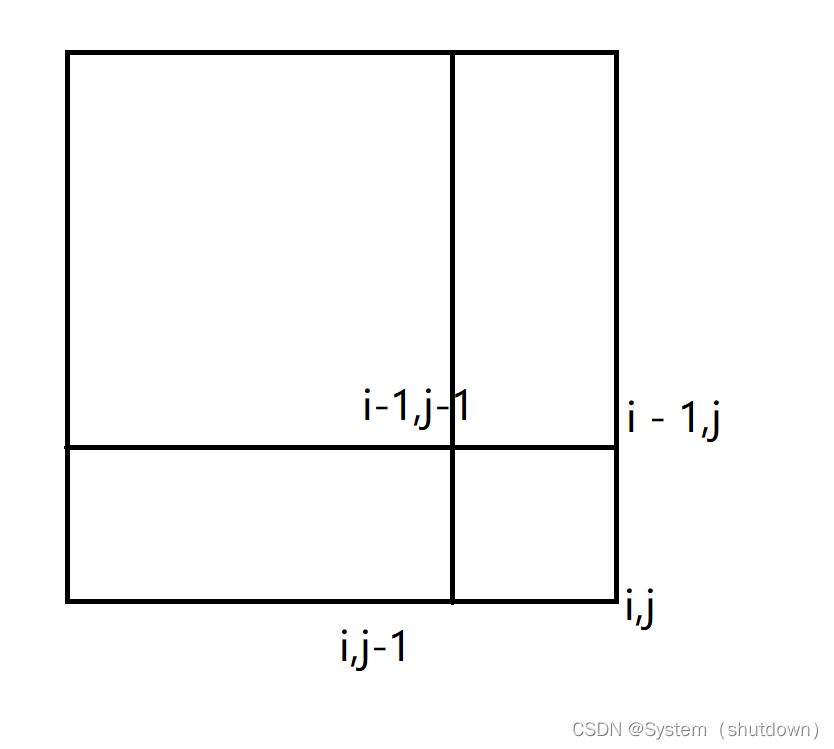
标红的区域代表的就是区间[i-1,j-1]的的和

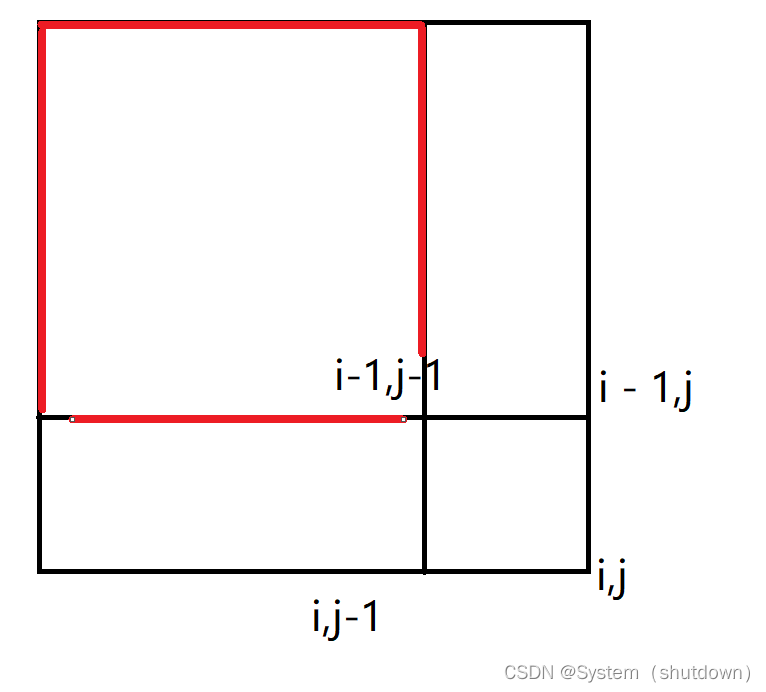
标绿的区域就是区间[i-1,j]的和

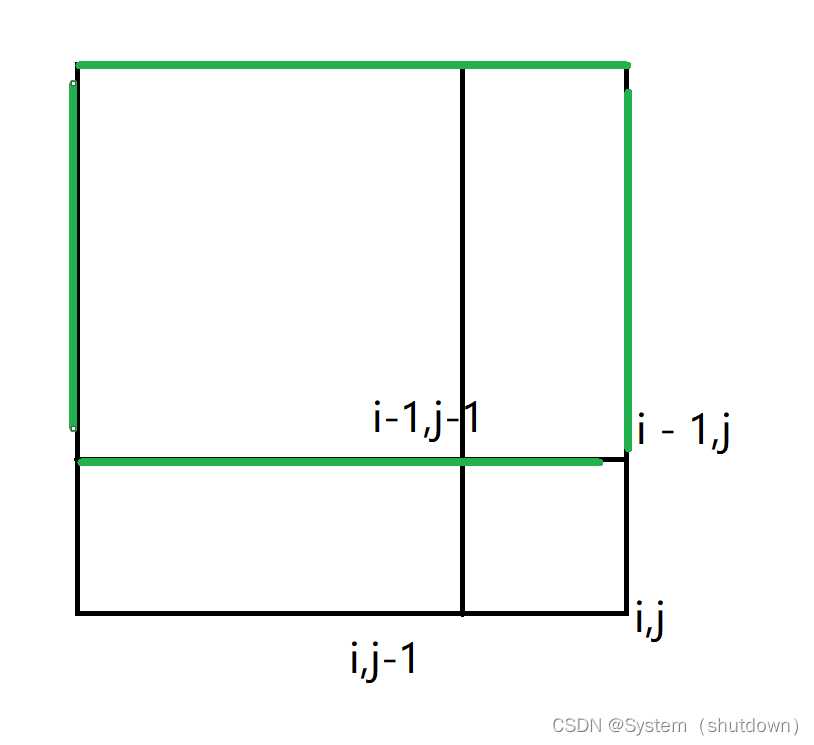
标蓝的区域就是区间[i,j-1]的和

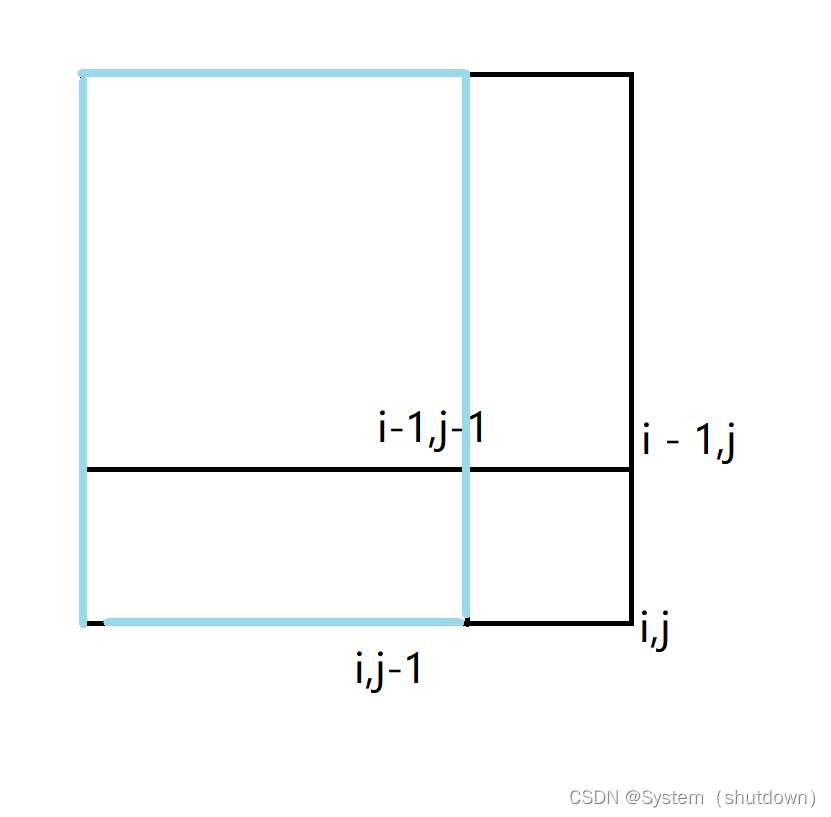
这个整体代表的就是区间[i,j]的和

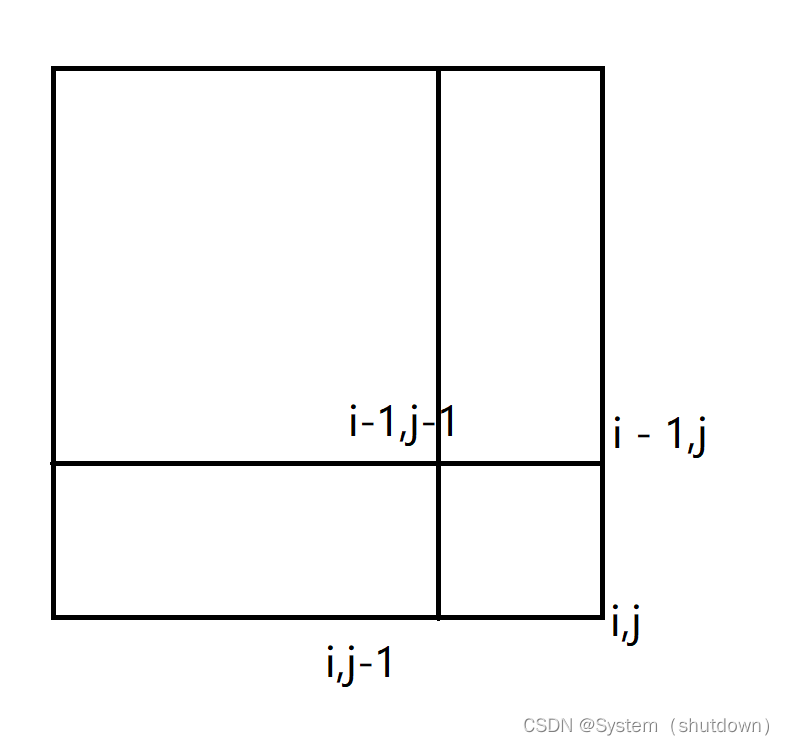
由此可以看出，在计算s[i,j]的和的时候，是不是把区间s[i-1,j-1]多算了一次，所以应该把s[i-1,j-1]减去一次，就能得到区间s[i,j]正确的区间和了。

2.完整代码

#include <iostream>using namespace std;const int N = 1e3 + 10;int a[N][N], s[N][N];int main()
{int n, m, q;cin >> n >> m >> q;for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){cin >> a[i][j];}}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];}}while (q--){int x1, x2, y1, y2;cin >> x1 >> y1 >> x2 >> y2;cout << s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1] << endl;}return 0;
}

例题acwing796.子矩阵的和

---

以上就是对前缀和的介绍，希望对大家有帮助。