平衡二叉树

首先生成一个二叉排序树

左旋转

右旋转

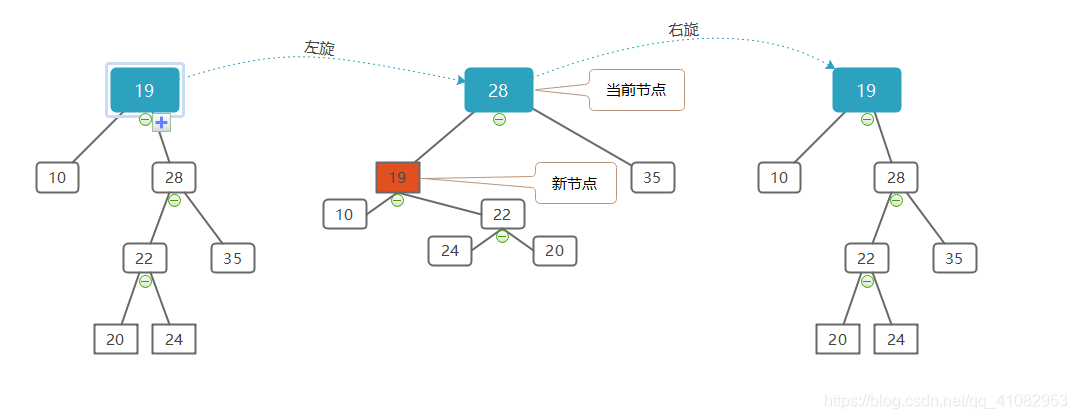
双旋转：

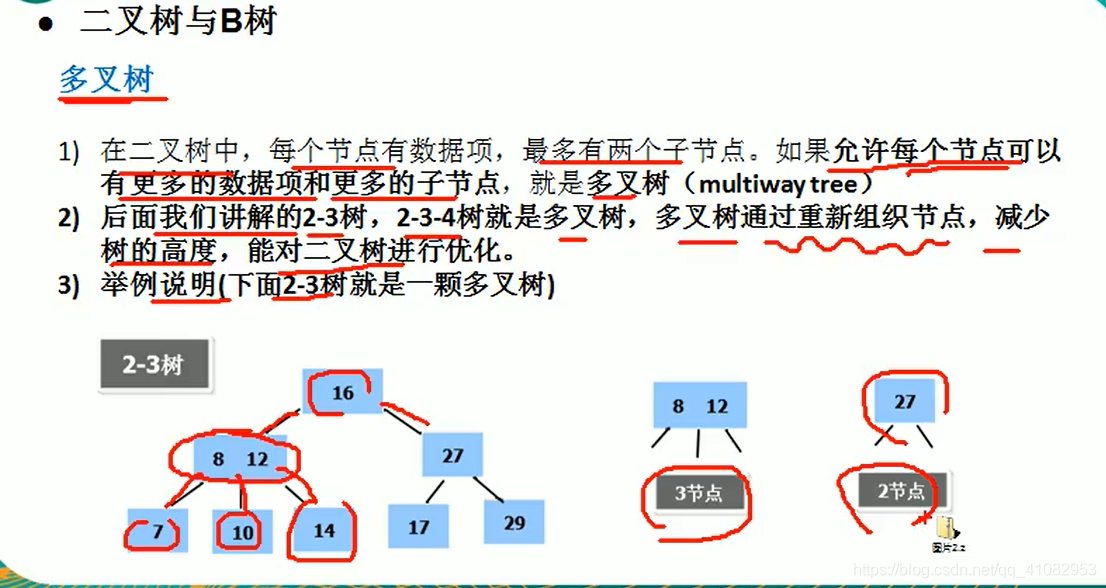
多叉树

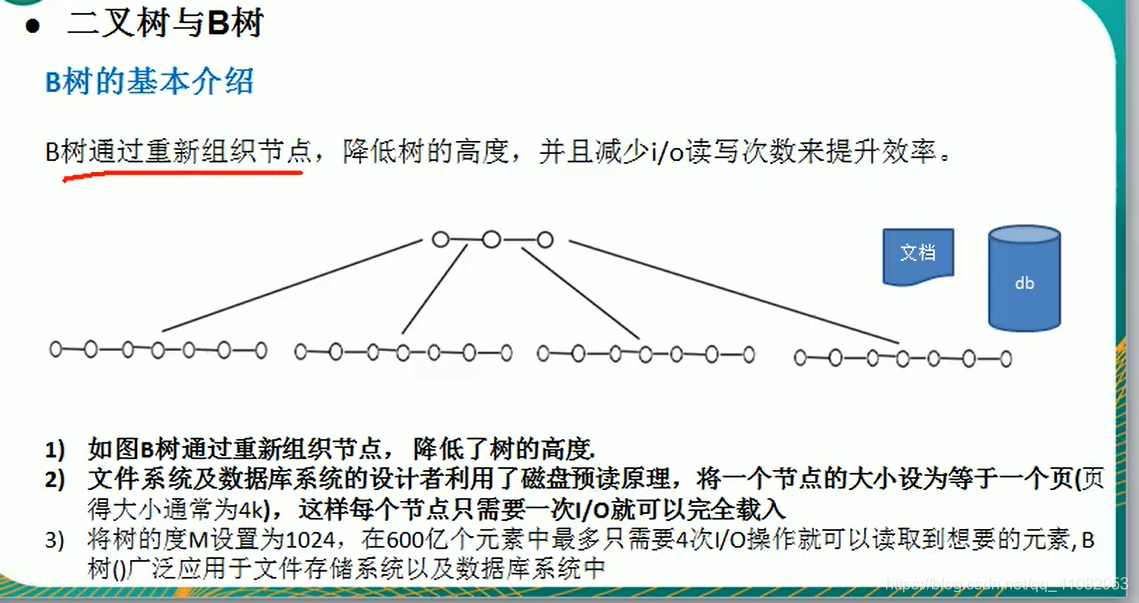
B树

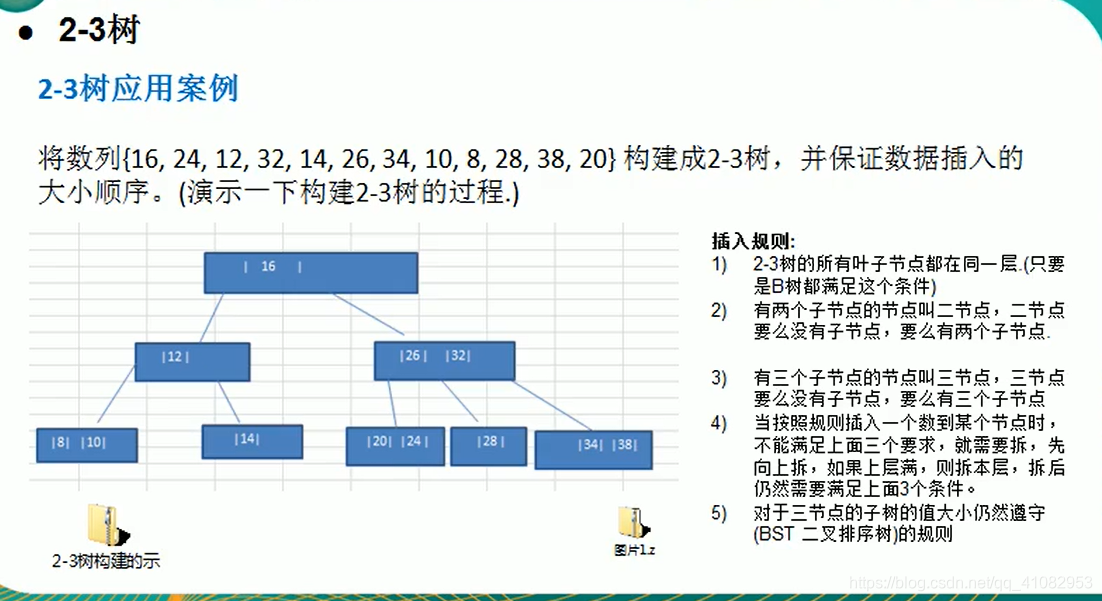
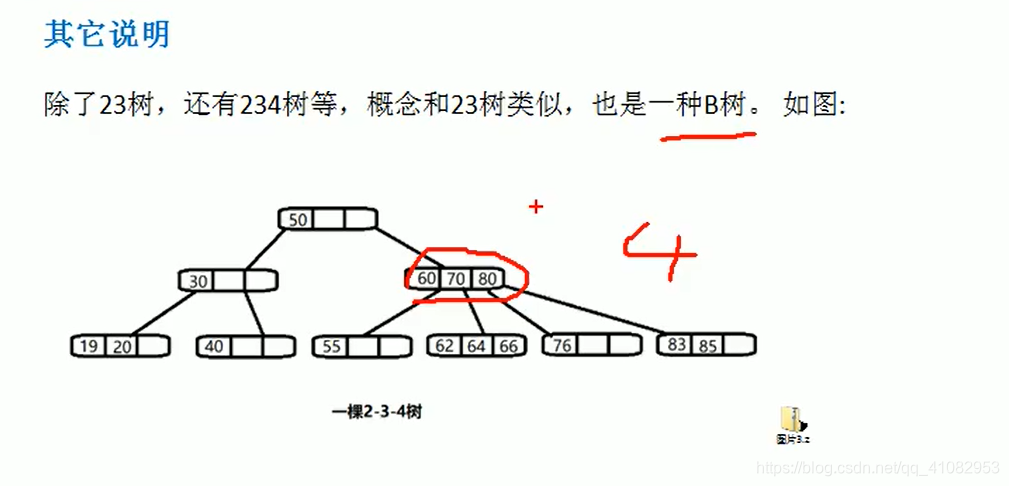
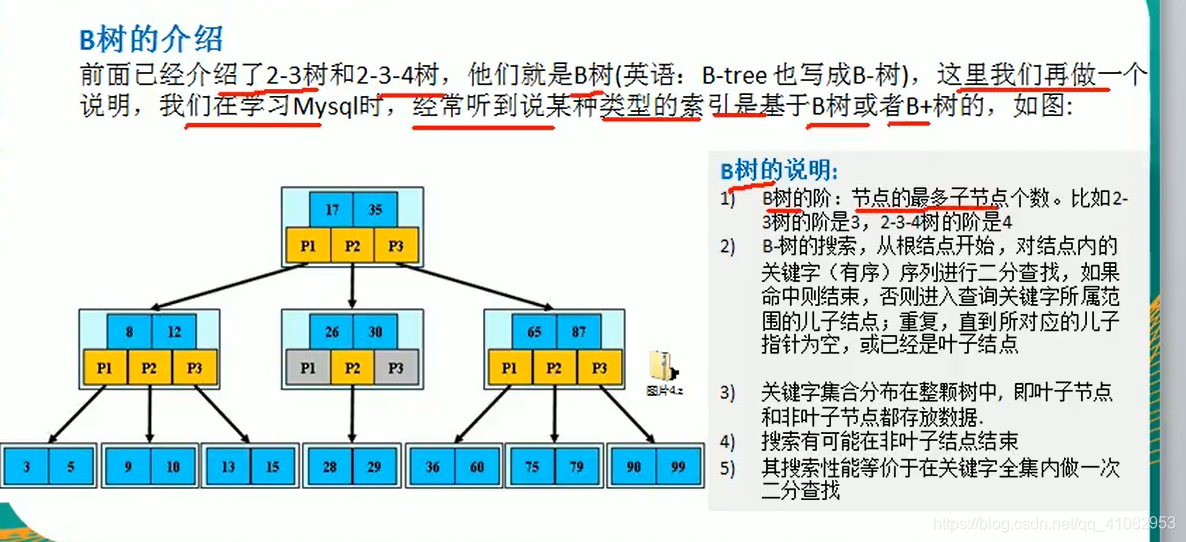
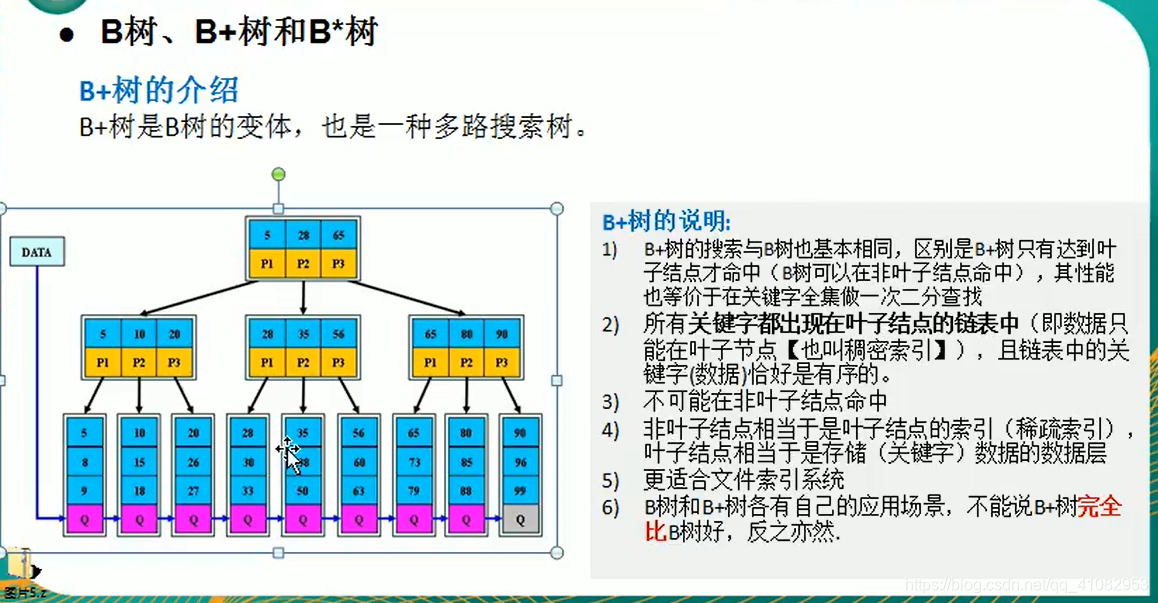
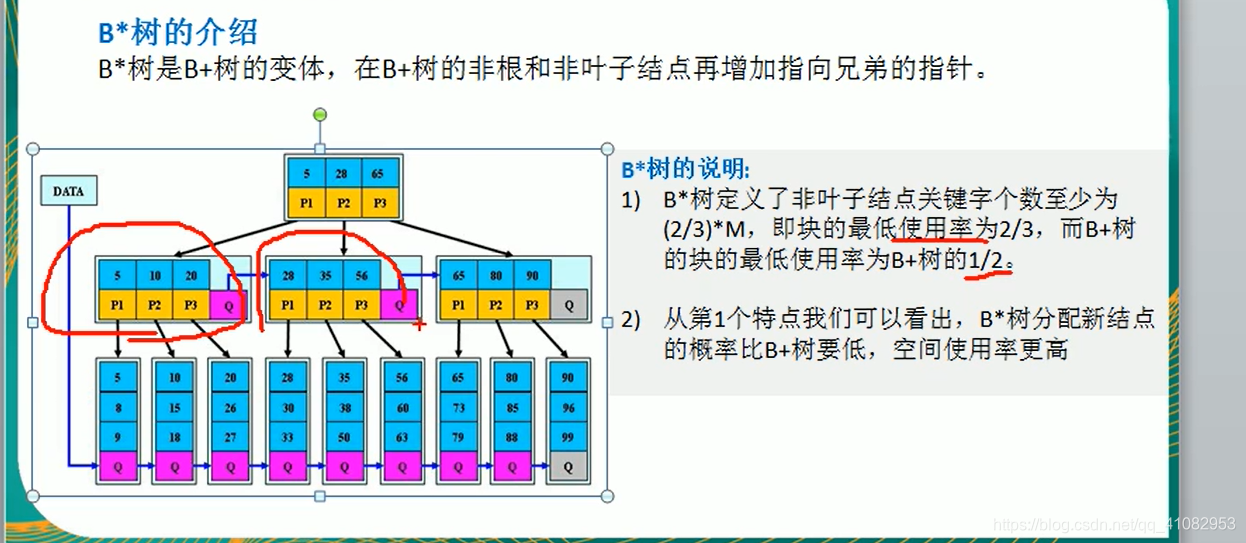
二叉排序树的插入和删除的代码：删除后没有判断在平衡的操作：

import java.util.*;
// 二叉平衡排序树
//1. 创建一个二叉排序树
//2. 删除其中某个节点
public class AVLTree {public static void main(String[] argv){AVLTreeList tree = new AVLTreeList();
//        tree.add(19);
//        tree.add(10);
//        tree.add(28);
//        tree.add(22);
//        tree.add(35);
//        tree.add(20);
//        tree.add(24);tree.add(10);tree.add(9);tree.add(8);tree.add(7);tree.add(6);tree.add(5);tree.add(4);tree.infixOrder();tree.sortOrder();
//        // 树的高度
//        System.out.println(tree.getRoot().height());
//        // 左子节点的高度
//        System.out.println(tree.getRoot().leftHeight());
//        // 右子节点的高度
//        System.out.println(tree.getRoot().rightHeight());//        // 查找要删除的节点
//        System.out.println(tree.searchDelParent(8));
//        // 查找要删除的父节点
//        System.out.println(tree.search(8));
//        System.out.println(tree.searchDelParent(7));// 删除叶子节点 10tree.delNode(10);tree.infixOrder();tree.sortOrder();// 删除单叶子节点9tree.delNode(9);tree.infixOrder();tree.sortOrder();// 删除双子节点5tree.delNode(5);tree.infixOrder();tree.sortOrder();// 删除根节点7tree.delNode(7);tree.infixOrder();tree.sortOrder();}}
// AVLTree管理
class AVLTreeList{// 根节点private Node root;public Node getRoot(){return root;}// 添加节点public void add(int num){if(root==null){root = new Node(num);}else{root.add(num);}//System.out.println(num+":");//this.infixOrder();//this.sortOrder();}// 中序遍历二叉树public void infixOrder(){if(root==null){return;}else{root.infixOrder();}System.out.println();}// 层序遍历二叉树：广度优先搜索public void sortOrder(){// List<List<Integer>> ret = new ArrayList <>();Queue<Node> queue = new LinkedList<>();queue.offer(this.root);while(!queue.isEmpty()){int length = queue.size();for(int i =0;i<length;i++){Node node = queue.poll();if(node.left!=null){queue.offer(node.left);}if(node.right!=null){queue.offer(node.right);}System.out.print(node+",");}System.out.println();}}// 查找要删除的节点public Node search(int num){if(root==null){return null;}return root.search(num);}// 查找要删除节点的父节点public Node searchDelParent(int num){if(root==null){return null;}return root.searchParent(num);}// 删除右子树最小的值并返回public int delRightTreeMin(Node rightTree){while(rightTree.left!=null){rightTree = rightTree.left;}delNode(rightTree.num);return rightTree.num;}// 删除节点：public void delNode(int num){if(root==null){return;}// 查找要删除节点Node delNode = search(num);if(delNode == null){return;}// 如果找到了要删除的节点 如果只有一个root节点，那么找到的就是root，直接删除if(root.left==null&&root.right==null){root = null;return;}// 找到删除节点的父节点Node delNodeParent = searchDelParent(num);// 如果删除节点是叶子节点// 如果删除节点有两个子节点// 如果删除节点只有一个节点if(delNode.left==null&&delNode.right==null){if(delNodeParent.left!=null&&delNodeParent.left==delNode){delNodeParent.left = null;}else if ((delNodeParent.right!=null)&&(delNodeParent.right==delNode)){delNodeParent.right = null;}}else if(delNode.left!=null&&delNode.right!=null){delNode.num = delRightTreeMin(delNode.right);}else{if(delNode.left!=null){if(delNodeParent!=null){if (delNodeParent.left==delNode) {delNodeParent.left=delNode.left;}else{delNodeParent.right=delNode.left;}}else{root = delNode.left;}}else{if(delNodeParent!=null){if (delNodeParent.left==delNode) {delNodeParent.left=delNode.right;}else{delNodeParent.right=delNode.right;}}else{root = delNode.right;}}}}
}// 二叉树节点
class Node implements Comparable<Node> {// 左右子节点指针public Node left;public Node right;// 存放的数据public int num;// Node构造器重载Node(int num){this.num = num;}// 返回树的高度public int height(){return Math.max(left==null?0:left.height(),right==null?0:right.height()) + 1;}// 返回左子树高度public int leftHeight(){if(left==null){return 0;}else{return left.height();}}// 返回右子树高度public int rightHeight(){if(right==null){return 0;}else{return right.height();}}// 添加节点：注意要写为添加Node而不是numpublic void add(int num){// 添加一个节点if(num>this.num){if(this.right==null){this.right = new Node(num);}else{this.right.add(num);}}else{if(this.left==null){this.left = new Node(num);}else{this.left.add(num);}}// 添加完节点后平衡二叉树// 左旋：如果左节点少于右节点高度，那么进行左旋if(this.leftHeight()+1<this.rightHeight()){// 如果右子树需要先进行右旋if(this.right!=null&&this.right.leftHeight()>this.right.rightHeight()){this.right.rightRotate();}leftRotate();return; // 可以先进行return没必要进行后面操作了}// 右旋if(this.leftHeight()>this.rightHeight()+1){// 如果左子树需要左旋要进行左旋if(this.left!=null&&this.left.rightHeight()>this.left.leftHeight()){this.left.leftRotate();}rightRotate();}}// 左旋public void leftRotate(){// 第一步新建一个临时节点Node temp = new Node(this.num);// 临时节点左子节点指向不变temp.left = this.left;// 临时节点右子节点指向当前节点的右子节点的左子节点temp.right = this.right.left;// 第二步当前节点的值设置为右子节点的值this.num = this.right.num;// 当前节点的左子节点指向新建的临时节点this.left = temp;// 当前节点的右子节点指向当前节点的右子节点的右子节点this.right = this.right.right;}// 右旋public void rightRotate(){Node temp = new Node(this.num);temp.right = this.right;temp.left = this.left.right;this.num = this.left.num;this.left = this.left.left;this.right = temp;}// 查找要删除的节点public Node search(int value){if(value == this.num){return this;}else if(value > this.num ){if(this.right==null){return null;}return this.right.search(value);}else {if (this.left==null){return null;}return this.left.search(value);}}// 查找父节点public Node searchParent(int num){if (this.left!=null&&num==this.left.num || this.right!=null&&num==this.right.num){return this;}else if(num<this.num&&this.left!=null){return this.left.searchParent(num);}else if(num>=this.num&&this.right!=null){return this.right.searchParent(num);}else{return null;}}// 比较节点大小的方法@Overridepublic int compareTo(Node o){return this.num-o.num;}// 打印节点@Overridepublic String toString(){return "Node:" + this.num;}// 中序遍历public void infixOrder(){// 先打印左子节点if(this.left!=null){this.left.infixOrder();}// 打印本节点System.out.print(this.num+",");// 打印右子节点if(this.right!=null){this.right.infixOrder();}}}