E - Alice, Bob, Oranges and Apples
CodeForces - 586E感觉是不是会跟橘子苹果之间的比例有什么关系
搜题解的时候发现了 Stern-Brocot tree
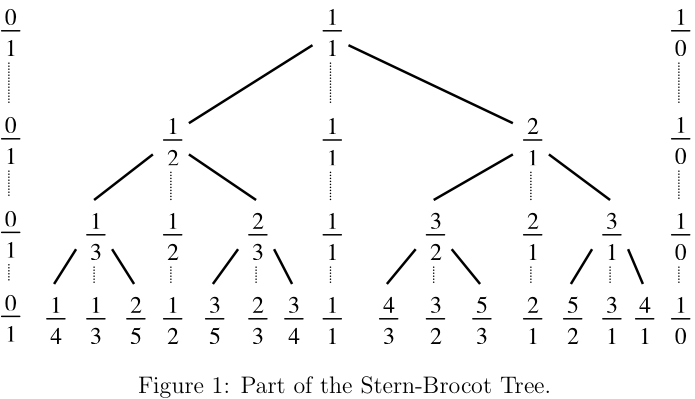
长这样 和我想的那个很类似 可开心了
但是后来看不懂题解什么意思
关于Stern树的一点结论是 每一层相邻的两个数a/b 和 c/d 可以得到下面一层的数(a+c)/(b+d)
而且分子分母一定是互质的
后来自己找规律 觉得如果x比y小就需要一次B操作 下面是代码
TLE on test 10
#include<iostream>
#include<stdio.h>
#include<algorithm>
#include<cmath>
#include<cstring>using namespace std;long long x, y;long long gcd(long long x, long long y)
{return (y == 0)? x : gcd(y, x % y);
}int main()
{while(scanf("%I64d%I64d", &x, &y) != EOF){if(gcd(x, y) != 1){cout<< "Impossible\n";}else{long long timea = 0, timeb = 0;while(abs(x-y) >= 1){if(x < y){if(timea){cout<<timea<<"A";timea = 0;}timeb++;y -= x;}else{if(timeb){cout<<timeb<<"B";timeb = 0;}timea++;x -= y;}}if(timea)cout<<timea<<"A"<<endl;if(timeb)cout<<timeb<<"B"<<endl;}}return 0;
}
T完了以后觉得自己真的怎么还是这么傻
也不估一下复杂度
又找到了新的题解 说直接模拟的
还是不太懂
先附在这里 晚点看
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;void work()
{LL a, b;scanf("%I64d%I64d", &a, &b);if(__gcd(a, b) != 1) {printf("Impossible\n");return;}while(a && b) {if(a < b) {LL t = b / a;if(a * t == b) printf("%I64dB", t-1);else printf("%I64dB", t);b -= t * a;}else {LL t = a / b;if(b * t == a) printf("%I64dA", t-1);else printf("%I64dA", t);a -= t * b;}}printf("\n");
}int main()
{
//freopen("data", "r", stdin);work();return 0;
}找trader问了一下思路 突然好像理解了!!!
先假设某一个状态橘子苹果数量是A和B且A<B
那么B肯定是由k次上一状态的A加上上一状态的B得到的
所以可以理解 A操作的次数就是B/A次 如果没有余数说明过头了要减1
