最近邻算法可以基于某数据实例的邻居来判定该实例的类型。k最近邻算法从距离该实例最近的k个邻居中找出最具代表性的类型，并将其赋给该数据实例。

本问将介绍k-NN算法的基础知识，并通过一个简单的例子——Mary对温度的偏好来理解和实现k-NN算法。在意大利的示例地图上，您将学习如何选择正确的k值，以使算法正确执行并达到最高的准确率。您将从房屋偏好的例子中学习如何重新调整k-NN算法的数值参数。在文本分类的例子中，您将学习如何选择一个好的标准来衡量数据点之间的距离，以及如何消除高维空间中不相关的维度以保证算法的正确执行。

1.1　Mary对温度的感觉

举个例子，如果Mary在10℃的时候感觉冷，但在25℃的时候感觉热，那么在22℃的房间里，最近邻算法猜测她会感到温暖，因为22℃比10℃更接近25℃。

前面的例子可以知道Mary什么时候感觉到热或冷，但当Mary被问及是否感到热或冷时，风速也是一个影响因素，如表1-1所示。

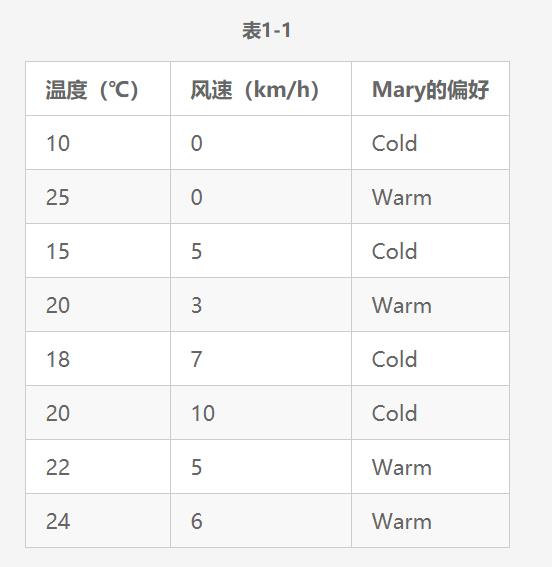
将该数据在图中表示，结果如图1-1所示。

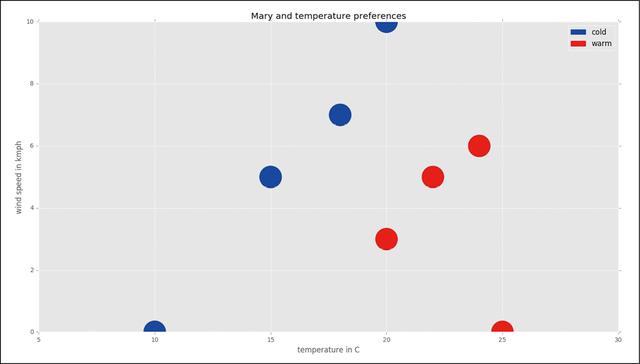
图1-1

现在，假设用1-NN算法判断Mary处在温度为16℃、风速为3km/h情况下的感觉，如图1-2所示。

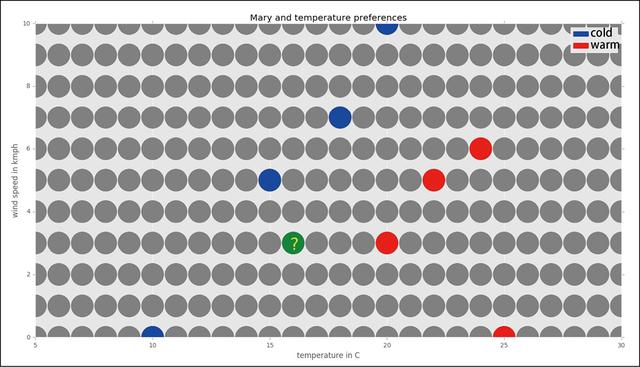
图1-2

简单起见，这里使用曼哈顿距离来度量网格上邻居节点之间的距离。节点N2=(x2，y2)与节点N1=(x1，y1)的曼哈顿距离d-Man定义为dMan=| x1 - x2 | + | y1 - y2 |。

现在用邻居间的距离来标记网格，如图1-3所示。看看哪个已知类型的邻居节点最接近目标节点。

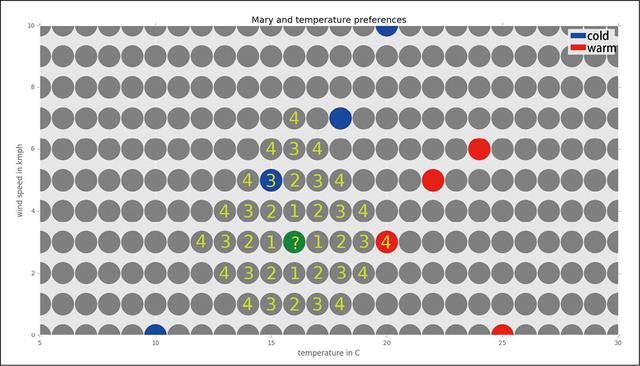
图1-3

很明显，最近邻居(类型已知)的温度为15℃(蓝)，风速为5km/h。它与目标节点的距离是3个单位，其类型是蓝色的(冷)。最接近的红色(热)邻居与目标节点相距4个单位。由于我们使用的是1邻近算法，所以我们只关注最近的一个邻居，因此目标节点的类型应该是蓝色的(冷)。

将上述过程作用于每个数据点，得到的完整图形如图1-4所示。

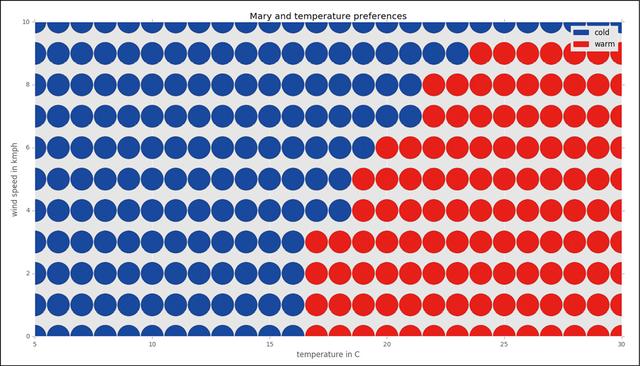
图1-4

请注意，有时某个数据点可被两个相同距离的已知类别(20℃和6km/h)隔开。在这种情况下，可以只选择其中一类或忽略这些边界情况。实际结果取决于算法的实现方式。

1.2　实现k最近邻算法

这里用Python实现k-NN算法来查找Mary的温度偏好。本节的最后还把Mary例子中由k-NN算法生成的数据可视化。完整可编译代码可以在本书提供的源代码中找到。最重要的部分如下：

# source_code/1/mary_and_temperature_preferences/knn_to_data.py# 将knn算法作用于输入数据# 假定输入的文本文件通过行来分隔# 每条数据都包含有温度、风速、类别(冷/热)import syssys.path.append('..')sys.path.append('../../common') import knn # noqaimport common # noqa# Program start# E.g. "mary_and_temperature_preferences.data"input_file = sys.argv[1]# E.g. "mary_and_temperature_preferences_completed.data"output_file = sys.argv[2]k = int(sys.argv[3])x_from = int(sys.argv[4])x_to = int(sys.argv[5])y_from = int(sys.argv[6])y_to = int(sys.argv[7])data = common.load_3row_data_to_dic(input_file)new_data = knn.knn_to_2d_data(data, x_from, x_to, y_from, y_to, k) common.save_3row_data_from_dic(output_file, new_data)# source_code/common/common.py# ***通用例程与函数的库***def dic_inc(dic, key): if key is None: pass if dic.get(key, None) is None: dic[key] = 1 else: dic[key] = dic[key] + 1# source_code/1/knn.py# ***实现knn算法的库***def info_reset(info): info['nbhd_count'] = 0 info['class_count'] = {}# 通过坐标x、y找到邻居的类型(假如该类型是已知的)def info_add(info, data, x, y): group = data.get((x, y), None) common.dic_inc(info['class_count'], group) info['nbhd_count'] += int(group is not None)# 将使用曼哈顿距离的k最近邻算法应用于2d数据# 数据字典的键是2d坐标，值是相应的类型# x、y是整数2d坐标，其范围为[x_from,x_to]×[y_from,y_to]def knn_to_2d_data(data, x_from, x_to, y_from, y_to, k): new_data = {} info = {} # 遍历整数坐标系的每个值 for y in range(y_from, y_to + 1): for x in range(x_from, x_to + 1): info_reset(info) # 从0开始，计算单位距离中每个类组的邻居数，直到至少找到具有已知类的k个邻居 for dist in range(0, x_to - x_from + y_to - y_from): # 计算[x, y]的所有邻居 if dist == 0: info_add(info, data, x, y) else: for i in range(0, dist + 1): info_add(info, data, x - i, y + dist - i) info_add(info, data, x + dist - i, y - i) for i in range(1, dist): info_add(info, data, x + i, y + dist - i) info_add(info, data, x - dist + i, y - i) # 如果它们到[x，y]的距离是相同的，那么最近的邻居可能多于k个。 # 当邻居数大于k个时，就从循环中跳出 if info['nbhd_count'] >= k: break class_max_count = None # 从k个最近的邻居中选择出现次数最多的类型 for group, count in info['class_count'].items(): if group is not None and (class_max_count is None or count > info['class_count'][class_max_count]): class_max_count = group new_data[x, y] = class_max_countreturn new_data

[输入]

上面的程序将使用下面的文件作为输入数据。该文件包含Mary对温度的已知偏好数据：

# source_code/1/mary_and_temperature_preferences/marry_and_temperature_preferences.data10 0 cold25 0 warm15 5 cold20 3 warm18 7 cold20 10 cold22 5 warm24 6 warm

[输出]

我们在mary_and_temperature_preferences.data这一数据集上执行k =1的k-NN算法。该算法对整数坐标系上的所有数据点进行分类，这一长方形坐标系的范围为(30-5=25)， (10-0=10)，因此总共有(25+1) × (10+1) 即 286个整数点(加一个边界点数)。使用wc命令可以发现输出文件正好包含286行，每个点有一个数据项。使用head命令可以显示输出文件的前10行。下一部分将输出文件中的所有数据可视化：

$ python knn_to_data.py mary_and_temperature_preferences.data mary_and_temperature_preferences_completed.data 1 5 30 0 10$ wc -l mary_and_temperature_preferences_completed.data 286 mary_and_temperature_preferences_completed.data$ head -10 mary_and_temperature_preferences_completed.data7 3 cold6 9 cold12 1 cold16 6 cold16 9 cold14 4 cold13 4 cold19 4 warm18 4 cold15 1 cold

[可视化]

本章前面所讲的可视化使用了matplotlib库。一个数据文件被加载，然后显示在一个分散的图中：

# source_code/common/common.py# 返回包含3个list的dict，分别包含x轴、 y轴与颜色数据def get_x_y_colors(data): dic = {} dic['x'] = [0] * len(data) dic['y'] = [0] * len(data) dic['colors'] = [0] * len(data) for i in range(0, len(data)): dic['x'][i] = data[i][0] dic['y'][i] = data[i][1] dic['colors'][i] = data[i][2] return dic# source_code/1/mary_and_temperature_preferences/mary_and_temperature_preferences_draw_graph.py import syssys.path.append('../../common') # noqaimport commonimport numpy as npimport matplotlib.pyplot as pltimport matplotlib.patches as mpatchesimport matplotlibmatplotlib.style.use('ggplot')data_file_name = 'mary_and_temperature_preferences_completed.data'temp_from = 5temp_to = 30wind_from = 0wind_to = 10data = np.loadtxt(open(data_file_name, 'r'), dtype={'names':('temperature','wind', 'perception'),  'formats': ('i4', 'i4', 'S4')})# 将类转换为在图中显示的颜色for i in range(0,len(data)): if data[i][2] == 'cold': data[i][2] = 'blue' elif data[i][2] == 'warm': data[i][2] = 'red' else: data[i][2] = 'gray'# 将数组转换为准备绘制函数的格式data_processed = common.get_x_y_colors(data)# 画图plt.title('Mary and temperature preferences')plt.xlabel('temperature in C')plt.ylabel('wind speed in kmph')plt.axis([temp_from, temp_to, wind_from, wind_to])# 将图例添加到图表blue_patch = mpatches.Patch(color='blue', label='cold')red_patch = mpatches.Patch(color='red', label='warm') plt.legend (handles=[blue_patch, red_patch])plt.scatter(data_processed['x'], data_processed['y'], c=data_processed['colors'], s=[1400] * len(data))plt.show()

1.3　意大利地区的示例——选择k值

该示例数据集包含了意大利及其周围地区的一些数据点(约1%)。蓝点代表水域，绿点代表陆地，白点代表未知类别。问题是根据已给出的部分信息来预测白色区域是代表水还是土地。

只包含1%地区数据的图片几乎是不见的。假如我们从意大利及周围地区获得大约为之前获得的33倍的数据，并将其绘制在图片中，结果如图1-5所示。

图1-5

[分析]

这里可以使用k-NN算法来解决该问题， k表示算法只关心目标的k个最近邻居。给定一个白点，如果其k个最近邻居大部分都代表水域，则它将被划分为水域；如果其k个最近邻居大部分都代表陆地，则它将被划分为陆地。算法将使用欧几里德距离：给定两个点X = [x0，x1]和Y = [ y0，y1]，它们的欧几里德距离定义为d= sqrt[(x0 - y0)2 +(x1 - y1)2 ]。

欧几里德距离是最常用的距离度量。在一张纸上给出两个点，它们的欧几里德距离就是用尺子测出的长度，如图1-6所示。

图1-6

选择一个k值以将k-NN算法应用于不完整的地区。由于目标点的类别根据其k个最近邻居中出现频次最高的类别来决定，因此k必须是奇数。下面分别将算法的k设为 1、3、5、7、9。

将该算法应用于不完整地区中的每个白点，得到的图如图1-7所示。

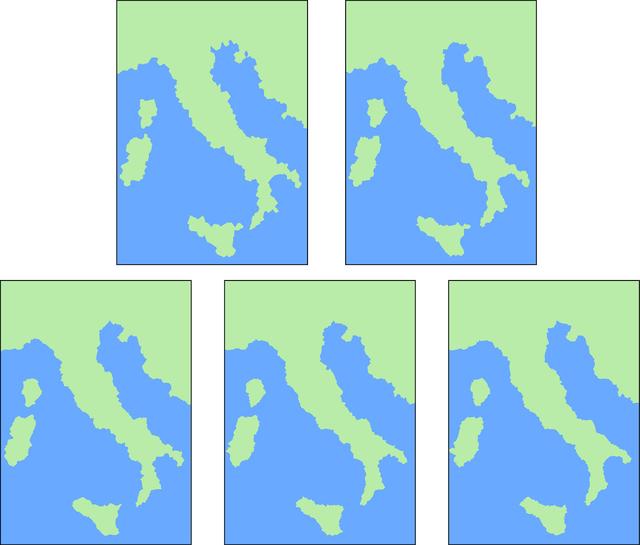
图1-7

正如你看到的，k值越高，结果越完整，边界越平滑。完整的意大利地区如图1-8所示。

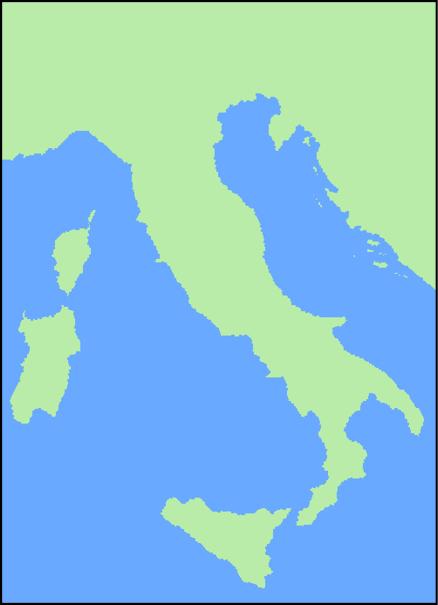
图1-8

这里可以使用真实的地图来计算错误分类点的百分比，以确定不同k值下k-NN算法的精度，如表1-2所示。

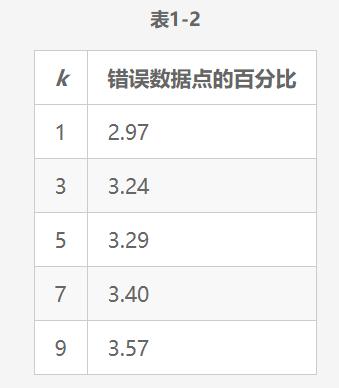
因此，对于这一特定类型的分类问题， k-NN算法在k = 1时精度最高(最小误差率)。

但是，现实生活中通常不会有完整的数据集或解决方案供你使用。此时我们需要根据不完整的可用数据来选择适合的k值。更多相关信息请参阅习题1.4。

-end-

喜欢的朋友欢迎转发到朋友圈