优秀网站建设设计/网络营销公司哪家好

动点问题为中考常考的问题。本文内容选自2020年宁夏中考数学压轴题，有两个三角板引发的重叠面积问题。难度不大。

【中考真题】

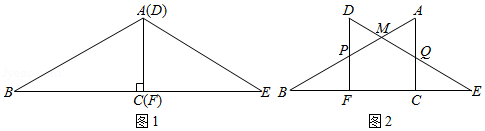
(2020•宁夏)如图(1)放置两个全等的含有30°角的直角三角板ABC与DEF(∠B＝∠E＝30°)，若将三角板ABC向右以每秒1个单位长度的速度移动(点C与点E重合时移动终止)，移动过程中始终保持点B、F、C、E在同一条直线上，如图(2)，AB与DF、DE分别交于点P、M，AC与DE交于点Q，其中AC＝DF，设三角板ABC移动时间为x秒．

(1)在移动过程中，试用含x的代数式表示△AMQ的面积；
(2)计算x等于多少时，两个三角板重叠部分的面积有最大值？最大值是多少？

【分析】
题(1)用x的代数式表示△AMQ的面积，由于AQ是竖直的，所以以它为底即可，然后过点M作AQ的高。表示出底和高即可。

题(2)重叠部分为五边形，可以用割补法进行求解。过点M作FC的高，分成两个全等的梯形；或者直接把△ABC的面积减去△AMQ与△BPF的面积即可。方法多样。

本题关键就是设未知数根据特殊角表示出线段长。【解答】解：(1)解：因为Rt△ABC中∠B＝30°，
∴∠A＝60°，
∵∠E＝30°，
∴∠EQC＝∠AQM＝60°，
∴△AMQ为等边三角形，
过点M作MN⊥AQ，垂足为点N．

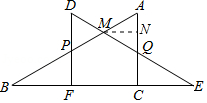
在Rt△ABC中，，
∴EF＝BC＝3，
根据题意可知CF＝x，
∴CE＝EF﹣CF＝3﹣x，
∴，
∴，而，
∴，

(2)由(1)知BF＝CE＝3﹣x，
∴
=
=
=
=，
所以当x＝2时，重叠部分面积最大，最大面积是．