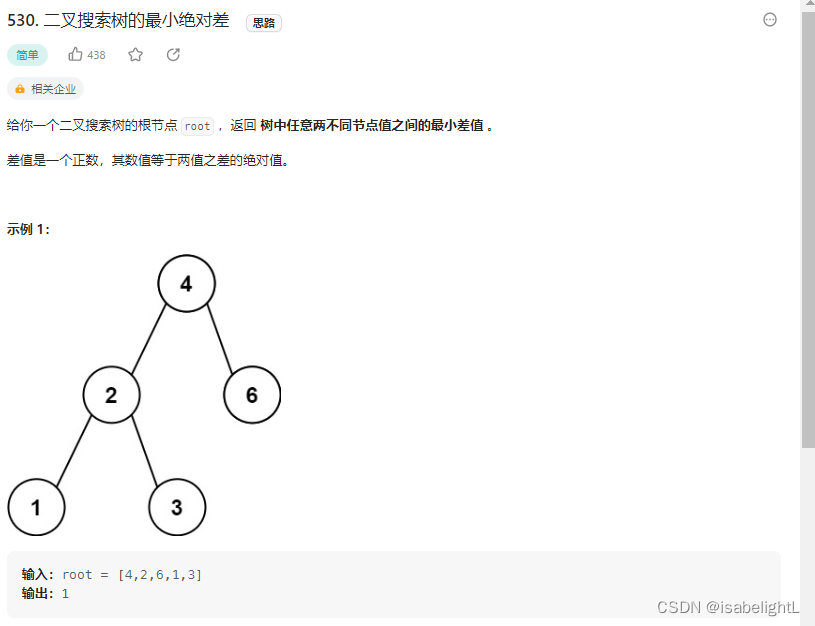
530.二叉搜索树的最小绝对差 

链接：代码随想录

需要领悟一下二叉树遍历上双指针操作，优先掌握递归

 第一次做，理解错误，认为只需要以节点为单位，认为由于是二叉搜索树，所以中序遍历一定是一个连续的有序序列，则只需要比较root->left->val和root->val。

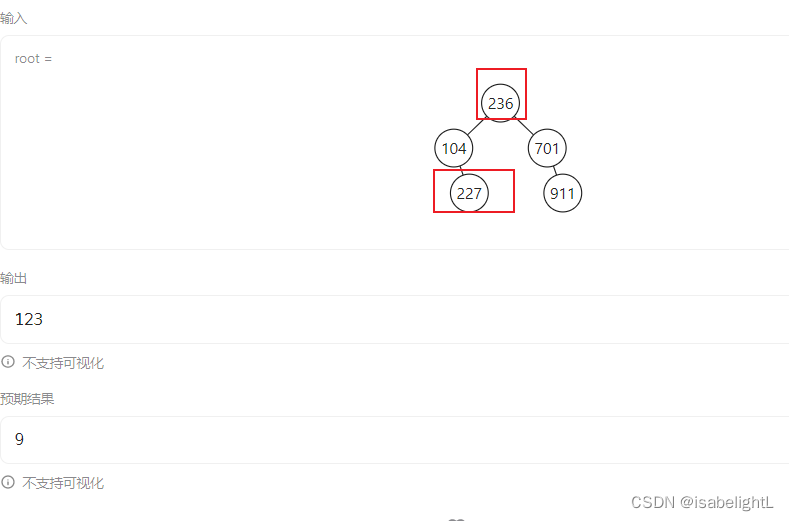
实际：理解错误，比如这种情况，要找到的是左子树的最大值，右子树的最小值，和root->val进行比较找最小值

，比如这种情况，仅仅以一个节点 为单位去比较它的左右节点是不全面的。

注：正确的方法是利用中序遍历，记录前一个结点，然后用pre和当下的root进行差值比较，更新最大值

递归做法：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*//*由于是二叉搜索树，所以中序遍历一定是一个连续的有序序列，则只需要比较root->left->val和root->val！理解错误，比如这种情况，要找到的是左子树的最大值，右子树的最小值，和root->val进行比较找最小值二叉搜索树采用中序遍历，其实就是一个有序数组。在一个有序数组上求两个数最小差值，这是不是就是一道送分题了。最直观的想法，就是把二叉搜索树转换成有序数组，然后遍历一遍数组，就统计出来最小差值了。*/
class Solution {
public:int minn=10e5+1;TreeNode *pre=nullptr;int getMinimumDifference(TreeNode* root) {helper(root);return minn;}void helper(TreeNode *root)//中序遍历改进{if(root!=nullptr){helper(root->left);if(pre!=nullptr)//在中序遍历的中间加入前一个结点与现有节点的比较{minn=min(minn,abs(pre->val-root->val));}pre=root;helper(root->right);}}
};

迭代做法，回忆中序遍历的迭代做法，利用栈：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*///中序遍历非递归
class Solution {
public:int getMinimumDifference(TreeNode* root) {int minn=10e5+1;stack<TreeNode*>sta;TreeNode *node=root;TreeNode* pre = NULL;while(!sta.empty()|| node!=nullptr){while(node!=nullptr){sta.push(node);node=node->left;}node=sta.top();/*中序遍历位置cout<<node->val<<endl;*/if(pre!=nullptr){minn=min(minn,abs(pre->val-node->val));}pre=node;sta.pop();node=node->right;}return minn;}
};

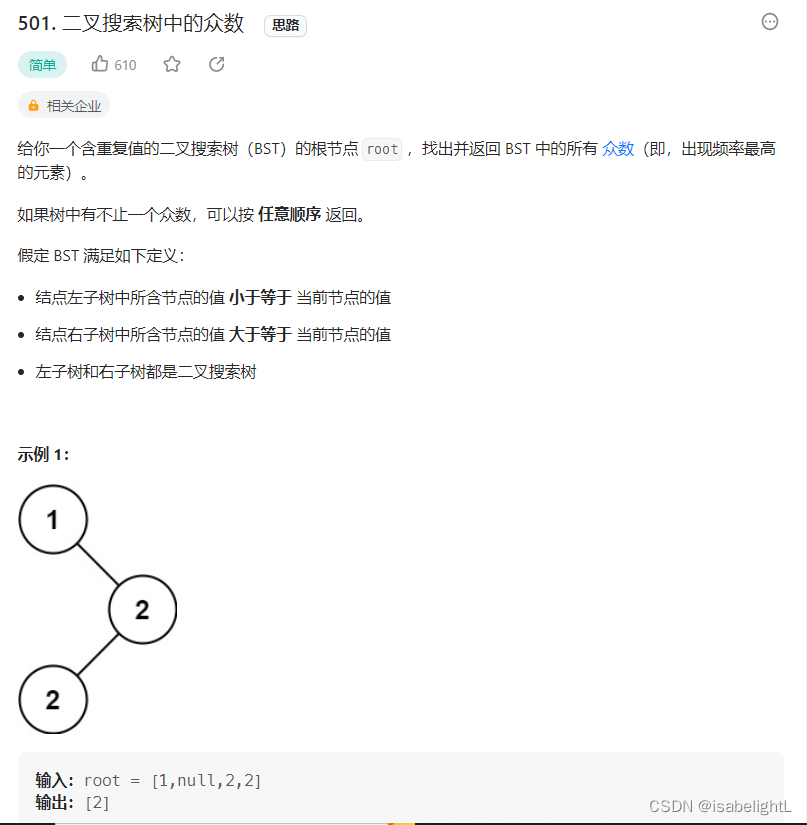
501.二叉搜索树中的众数 

链接：代码随想录

 

错误做法：错在递归结束时，pre停在最后一个节点，此时应该还有一个temp_cnt，需要最后和max_cnt 比较更新一下

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
// 结合前一道题来思考
public:int max_cnt=0;int temp_cnt=0;TreeNode *pre=nullptr;vector<int>v;vector<int> findMode(TreeNode* root) {helper(root);if(temp_cnt>max_cnt){while(!v.empty()){v.pop_back();};max_cnt=temp_cnt;v.push_back(pre->val);}else if(temp_cnt==max_cnt){max_cnt=temp_cnt;v.push_back(pre->val);}return v;}void helper(TreeNode *root){if(root!=nullptr){helper(root->left);if(pre!=nullptr){if(root->val==pre->val){temp_cnt++;}else{if(temp_cnt>max_cnt){v.clear();     // 很关键的一步，不要忘记清空result，之前result里的元素都失效了max_cnt=temp_cnt;v.push_back(pre->val);}else if(temp_cnt==max_cnt){max_cnt=temp_cnt;v.push_back(pre->val);}temp_cnt=1;}}pre=root;helper(root->right);}}
};

 改进后：

class Solution {
// 结合前一道题来思考
public:int max_cnt=1;int temp_cnt=1;TreeNode *pre=nullptr;vector<int>v;vector<int> findMode(TreeNode* root) {helper(root);if(temp_cnt>max_cnt){v.clear();     // 很关键的一步，不要忘记清空result，之前result里的元素都失效了max_cnt=temp_cnt;v.push_back(pre->val);}else if(temp_cnt==max_cnt){max_cnt=temp_cnt;v.push_back(pre->val);}return v;}void helper(TreeNode *root){if(root!=nullptr){helper(root->left);if(pre!=nullptr){cout<<pre->val<<" "<<root->val<<endl;if(root->val==pre->val)//如果和前一个结点值相等{temp_cnt++;}else//如果和前一个结点值不相等{if(temp_cnt>max_cnt){v.clear();     // 很关键的一步，不要忘记清空result，之前result里的元素都失效了max_cnt=temp_cnt;v.push_back(pre->val);}else if(temp_cnt==max_cnt){max_cnt=temp_cnt;v.push_back(pre->val);}temp_cnt=1;}}pre=root;helper(root->right);}}
};

最优的答案，这个答案不是计算上一个元素的连续相等元素个数，而是先pre=cur，然后计算比较cur->val和最大值，这样cur==nullptr时，能计算完所有元素的连续个数。

class Solution {
private:int count;int maxCount;TreeNode* pre;vector<int> result;void searchBST(TreeNode* cur) {if (cur == NULL) return ;searchBST(cur->left);       // 左// 中if (pre == NULL) { // 第一个节点count = 1;} else if (pre->val == cur->val) { // 与前一个节点数值相同count++;} else { // 与前一个节点数值不同count = 1;}pre = cur; // 更新上一个节点if (count == maxCount) { // 如果和最大值相同，放进result中result.push_back(cur->val);}if (count > maxCount) { // 如果计数大于最大值maxCount = count;result.clear();     // 很关键的一步，不要忘记清空result，之前result里的元素都失效了result.push_back(cur->val);}searchBST(cur->right);      // 右return ;}public:vector<int> findMode(TreeNode* root) {int count = 0; // 记录元素出现次数int maxCount = 0;TreeNode* pre = NULL; // 记录前一个节点result.clear();searchBST(root);return result;}
};作者：代码随想录
链接：https://leetcode.cn/problems/find-mode-in-binary-search-tree/solutions/425776/501-er-cha-sou-suo-shu-zhong-de-zhong-shu-bao-li-t/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

236. 二叉树的最近公共祖先 

同类型的题还有

剑指 Offer 68 - I. 二叉搜索树的最近公共祖先（链接：力扣）

剑指 Offer 68 - II. 二叉树的最近公共祖先(链接：力扣)

链接：代码随想录

 

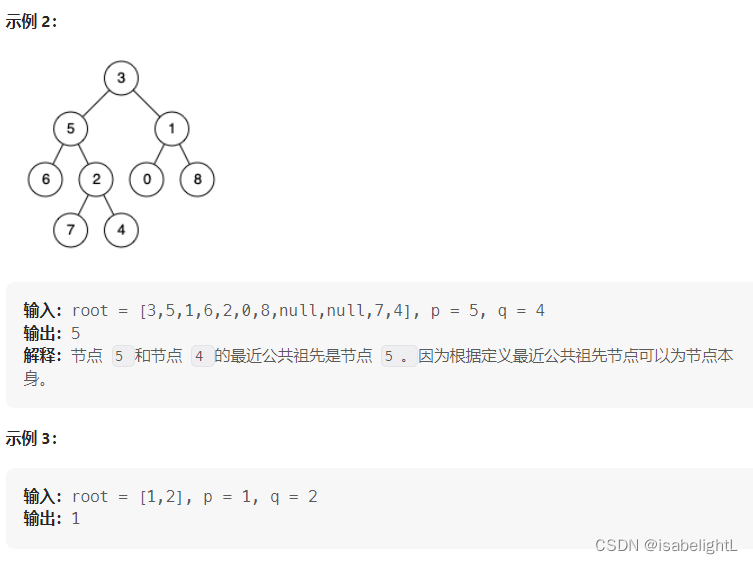
 完全没有了印象。。。灰溜溜的去看了题解.这道题显然是后序遍历，而且符合要求的节点要往上传，直到找到最近公共节

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*///首先是，这道题我好像做过。其次是，我没什么印象了。确实做过，剑指offer原题//二叉树,（一个节点也可以是它自己的祖先）。
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root==nullptr)return root;if(root==p||root==q)//当前遍历节点就是p或者q，直接返回当前节点{return root;}TreeNode *left=lowestCommonAncestor(root->left,p,q);//后序遍历，遍历左子树TreeNode *right=lowestCommonAncestor(root->right,p,q);//后序遍历，遍历右子树if(left!=nullptr && right!=nullptr)//左子树上找到p/q并传到了本节点，右子树也找到了，则本节点为公共节点，返回{return root;}else if(left!=nullptr){return left;}else{return right;}}
};

剑指 Offer 68 - I. 二叉搜索树的最近公共祖先 

链接：力扣

 

 自己的做法，通过查看官方题解，又掌握一种。发现官方题解的递归遍历和我的思路相同，但是代码更为简洁，同时代码逻辑更绕

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*///为了效率，简化了原本的二叉树的最近公共祖先
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root==nullptr||root==p ||root==q){return root;}TreeNode *left=nullptr,*right=nullptr;if(p->val<root->val ||q->val<root->val){left=lowestCommonAncestor(root->left,p,q);}if(p->val> root->val || q->val> root->val){right=lowestCommonAncestor(root->right,p,q);}if(left!=nullptr && right!=nullptr){return root;}else if(left!=nullptr){return left;}else{return right;}}
};

 官方解法：

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {//终止条件：不需要，因为官方给了均存在与树中的条件//          即老子现在肯定是这两个乖孙子的公共祖先//递推操作：//第一种情况：if(root.val>p.val&&root.val>q.val){//看看是不是都是左儿子的后代return lowestCommonAncestor(root.left,p,q);//是的话就丢给左儿子去认后代（继续递归）}//第二种情况：if(root.val<p.val&&root.val<q.val){//不是左儿子的后代，看看是不是都是右儿子的后代return lowestCommonAncestor(root.right,p,q);//是的话就丢给右儿子去认后代（继续递归）}//第三种情况：//左儿子和右儿子都说我只认识一个，唉呀妈呀，那就是老子是你们最近的祖先，因为老子本来就是你们的公共的祖先//现在都只认一个，那就是老子是最近的。//其实第三种才是题目需要找到的解，所以返回，拜托我的祖先们也传一下（递归回溯返回结果），我才是他们最近的公共曾爷爷return root;}