爬虫网站怎么做/广安百度推广代理商

(File IO): input:son.in output:son.out
时间限制: 1000 ms 空间限制: 128000 KB 具体限制
Goto ProblemSet

---

题目描述
$Hanks$ 博士是$BT$ ($Bio-Tech$，生物技术) 领域的知名专家，他的儿子名叫$Hankson$。现在，刚刚放学回家的$Hankson$ 正在思考一个有趣的问题。
今天在课堂上，老师讲解了如何求两个正整数$c1$ 和$c2$ 的最大公约数和最小公倍数。现在$Hankson$ 认为自己已经熟练地掌握了这些知识，他开始思考一个“求公约数”和“求公倍数”之类问题的“逆问题”，这个问题是这样的：已知正整数$a0,a1,b0,b1$，设某未知正整数$x$ 满足：
1． $x$ 和$a0$ 的最大公约数是$a1$；
2． $x$ 和$b0$ 的最小公倍数是$b1$；
$Hankson$ 的“逆问题”就是求出满足条件的正整数$x$。但稍加思索之后，他发现这样的$x$ 并不唯一，甚至可能不存在。因此他转而开始考虑如何求解满足条件的$x$ 的个数。请你帮助他编程求解这个问题。

---

输入
输入文件名为 $son.in$。第一行为一个正整数$n$，表示有$n$ 组输入数据。接下来的$n$ 行每行一组输入数据，为四个正整数$a0，a1，b0，b1$，每两个整数之间用一个空格隔开。输入数据保证a0 能被a1 整除，$b1$ 能被$b0$ 整除。

输出
输出文件 $son.out$ 共$n$ 行。每组输入数据的输出结果占一行，为一个整数。
对于每组数据：若不存在这样的 $x$，请输出$0$；
若存在这样的 $x$，请输出满足条件的$x$ 的个数；

---

样例输入
2
41 1 96 288
95 1 37 1776

样例输出
6
2

---

数据范围限制
对于 $50$的数据，保证有$1\le a0，a1，b0，b1\le 10000$ 且n≤100。
对于 $100$的数据，保证有$1\le a0，a1，b0，b1\le 2,000,000,000$ 且$n\le 2000$。

---

提示
第一组输入数据，$x$ 可以是$9、18、36、72、144、288$，共有$6$ 个。
第二组输入数据，$x$ 可以是$48、1776$，共有$2$ 个。

---

解题思路
由题得 ：
$gcd(x,a0)=a1$
$x\ast b0/gcd(x,b0)=b1;$

这样不好看
$x=p\ast a1;p=x/a1$
$a0=q\ast a1;q=a0/a1$

• 我们猜测 $p,q$的关系 ：$gcd(p,q)==1$
  设 $gcd(p,q)=K!=1$
  $p=k\ast n，q=k\ast m$
  所以 $x=k\ast n\ast a1，a0=k\ast m\ast a1$
  显然 $gcd(x,a0)=K\ast a1$ 不成立
  可以推广结论:
  $gcd(x,y)=k$ 则有 $gcd(x/k,y/k)=1$

所以

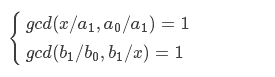
这样就很明朗了，枚举b1的因子记数就行了

---

代码

#include<iostream>
#include<cstring>
#include<iomanip>
#include<cmath>
#include<cstdio>
using namespace std;
int a0,a1,b0,b1,ans,n,p,q;
int work(int a,int b)
{if(a==1&&b==0||a==0&&b==1)return 1;elseif(a==0||b==0)return 0;elsereturn work(b%a,a);
}
int main(){freopen("son.in","r",stdin);freopen("son.out","w",stdout);scanf("%d",&n);for(int i=1;i<=n;i++){  scanf("%d%d%d%d",&a0,&a1,&b0,&b1);p=a0/a1,q=b1/b0;ans=0;for(int x=1;x*x<=b1;x++){if(b1%x==0){if(x%a1==0&&work(x/a1,p)&&work(b1/x,q)) ans++;int y=b1/x;if(y==x) continue;if(y%a1==0&&work(y/a1,p)&&work(b1/y,q)) ans++;}}printf("%d\n",ans);}return 0 ; 
}