南阳开网站制作/关键词优化顾问
1、问题描述
在8×8格的国际象棋上摆放8个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上。请借鉴递归算法设计理论,设计并实现一个八皇后问题求解算法,求解并输出所有正确的解,所有输出采用棋盘式,使用*代表皇后所在位置。
2、思路流程图
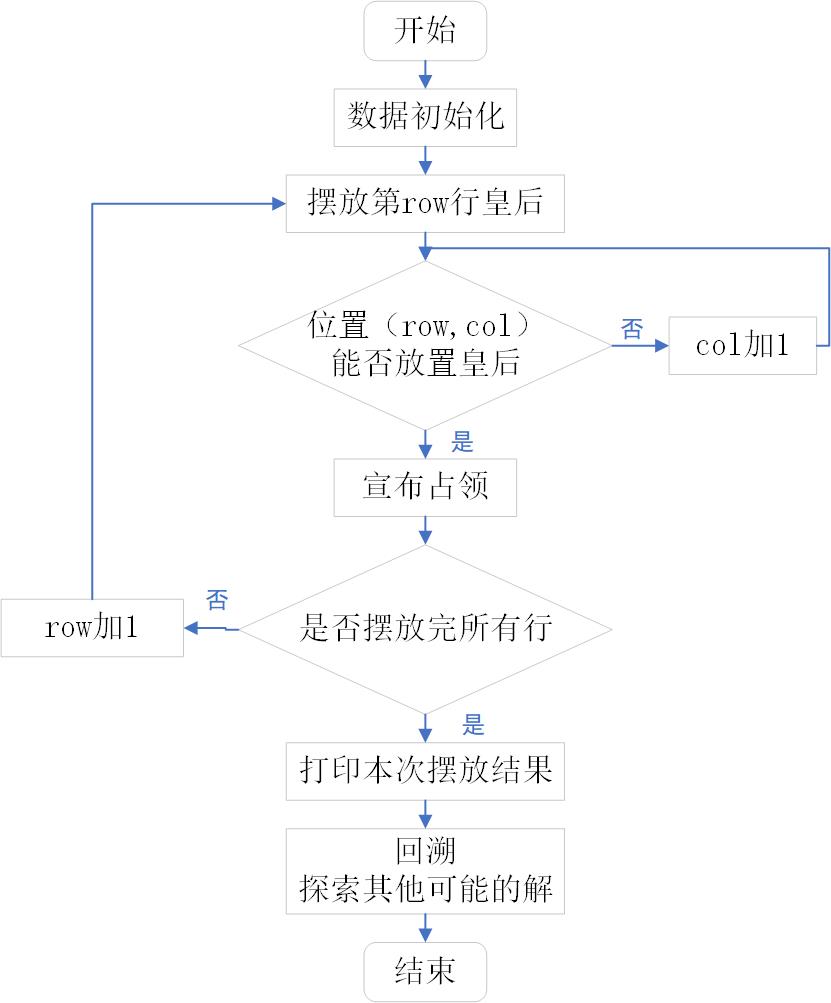

3、实验源码
#include<stdio.h>
#include<stdlib.h>
//全局变量数据初始化
int place[8] = { 0 }; //表示第n个皇后(第n行皇后)所占位置的列号,例如:place[1]=7 表示位置(1,7)摆放了皇后
int flag[8] = { 0 }; //表示第col列是否可占:0代表可占,1代表不可占
int diag1[15] = { 0 }; //表示主对角线是否可占,位置[i,j]的主对角线号为i-j+7
int diag2[15] = { 0 }; //表示次对角线是否可占,位置[i,j]的次对角线号为i+j
int number = 0; //用于统计结果的数量//打印摆放结果
void show_answer()
{int n, i, j;int table[8][8] = { 0 };number++;printf("第%d组结果:\n", number);for (n = 0; n < 8; n++)table[n][place[n]] = 1;for (i = 0; i < 8; i++){for (j = 0; j < 8; j++){if (table[i][j] == 1)printf("* ");elseprintf("%d ", table[i][j]);}printf("\n");}
}//摆放皇后
void queen(int row)
{int col;for (col = 0; col < 8; col++){if (flag[col] == 0 && diag1[row - col + 7] == 0 && diag2[row + col] == 0) //判断位置(i,j)是否可占{place[row] = col; //在第row行第col列摆放皇后flag[col] = 1; //占领第col列diag1[row - col + 7] = 1; //占领相应主次对角线diag2[row + col] = 1;if (row < 7) //8个皇后未摆放完毕queen(row + 1);else //8个皇后全部摆放完毕show_answer();//回溯继续找下一组解flag[col] = 0;diag1[row - col + 7] = 0;diag2[row + col] = 0;}}
}int main()
{queen(0);return 0;
}4、实验结果


