手机网站打不开的解决方法/市场营销的对象有哪些

（必要知识——2-3树）

通过2-3树理解红黑树

对2-3树有了一定理解之后，再回头看看红黑树的定义，将会从一个全新的角度去看待它们：

1. 节点是红色或黑色。
2. 根是黑色。
3. 所有叶子都是黑色（叶子是NIL节点）。
4. 每个红色节点必须有两个黑色的子节点。（从每个叶子到根的所有路径上不能有两个连续的红色节点。）
5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

下面会将红黑树的5个定义联系2-3树来联系（如果真正理解了2-3Tree，下面的过程非常容易）

节点是红色或黑色

2-3树的性质中，定义了它是由2-节点和3-节点所构成的一棵树型数据结构，而红黑树中，黑节点即为一个2-节点，而3-节点则是由一个红节点和一个黑节点组合而成的节点：

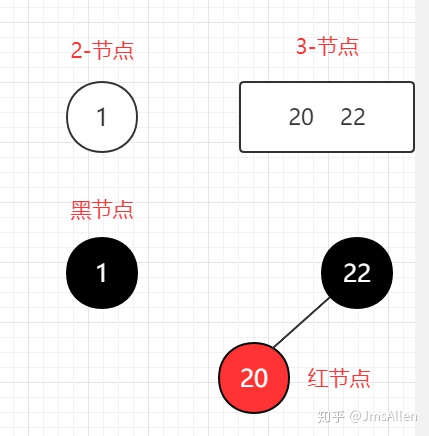
根是黑色

如果直接学习红黑树，这个定义会让人非常迷惑，为什么根节点就是黑色的？

根据上面的定义，红节点和黑节点会构成2-3树中的一个3-节点，那么：

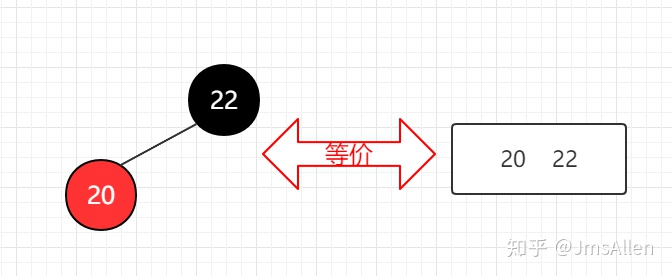
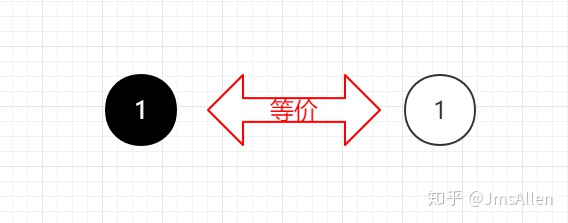
试想，在2-3树中，根节点要么是2-节点，要么是3-节点，则对应的红黑树的根节点无论如何都会是黑节点

所有叶子都是黑色

这个定义和二叉树中叶子节点的定义是不同的，红黑树中的叶子节点是指

• 一个节点的左（右）节点为空，将其定义为一个黑节点
• 一棵“空树”也可以是红黑树，而根据定义2——根节点为黑节点，这样也能符合红黑树的定义

每个红色节点必须有两个黑色的子节点

这一条定义与2-3树的定义联系理解，也很容易接受，试想在2-3树中，只有3-节点会对应红黑树中的红节点，一个红节点的子节点出现一个红节点，那么对应的2-3树中，就会出现一个4-节点，这样便违背了2-3树的定义，因此，每个红色节点必须有两个黑色的子节点

从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点

这条定义对于不理解2-3树直接学习红黑树的人而言，又是很难理解的性质，但通过2-3树可以了解到

• 2-3树是一棵完美平衡的树，那么每一个叶子节点的深度是相同的
• 2-3树由2-节点和3-节点构成，因此每个节点在对应的红黑树中必然包含一个黑节点

由此可以推断从任一节点到其每个叶子的所有简单路径都包含相同数目的黑节点

维护红黑树

破坏红黑树性质的操作依然是在添加和删除操作，红黑树的add()方法的代码可能是数据结构中最为复杂的代码之一，并且remove()相较下还要更复杂，但文章的主要目的是理解红黑树，因此本文只分析add()方法

红黑树的底层数据结构依然是使用的二分搜索树，因此实现的接口如下：

public interface IMap<K, V> {void add(K key, V value);V remove(K key);boolean contains(K key);V get(K key);void set(K key, V value);int getSize();boolean isEmpty();
}

红黑树的代码困难之处主要在于逻辑的分类讨论上，因此下面给出所有可能存在的添加操作，并对添加后的结构做出调整分析：

只有黑节点

对应于2-3树的2-节点，这种情况下，新加入的节点可以在左，也可以在右，前者不需要调整，形成2-3树中的3-节点，而后者就需要进行一次左旋转

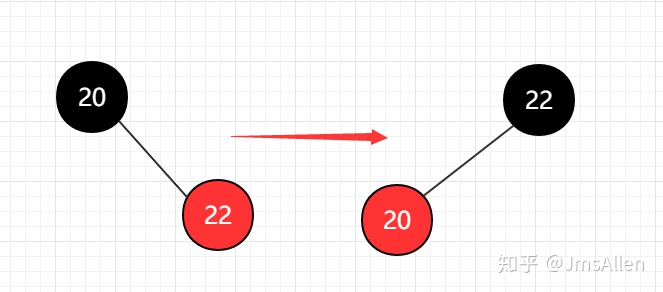
原因是在这个红黑树定义下，我们默认红节点是左倾的，这是为了方便整个逻辑的实现，当然定义为右倾也没问题

存在红——黑节点

上面的结构调整后，如果再添加一个大于黑节点的子节点，根据BST性质，结构如下：

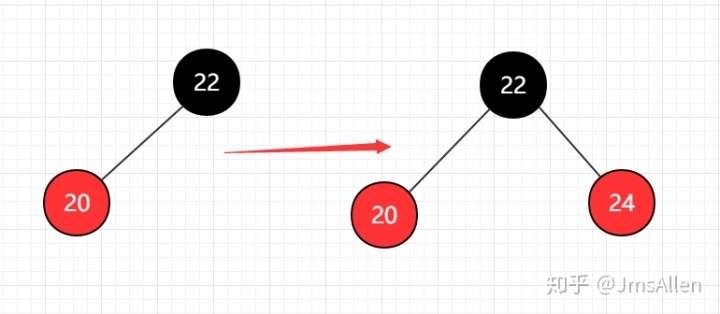
此时，相对于2-3树中的4-节点，则红黑树就应该做出颜色翻转操作：

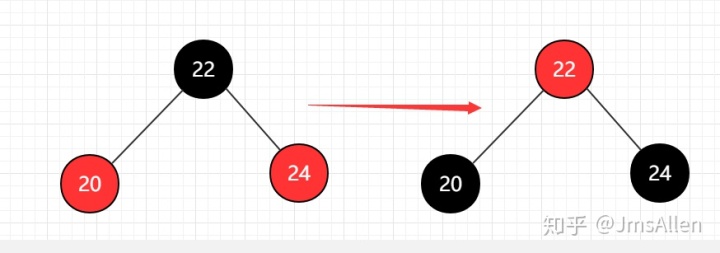
现在的父节点为红色，根据红黑树的性质，根节点为黑节点，但因为这仅仅是以个局部操作，后续会做出调整

除了上面的情况，还有一种添加红——黑节点的情况：

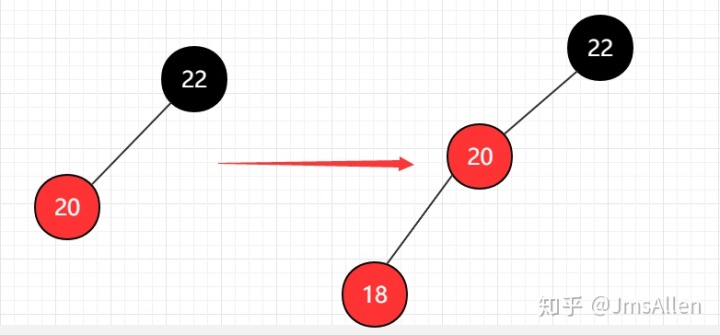
这种情况下，首先需要进行一次右旋转，然后再进行一次颜色翻转，如图：

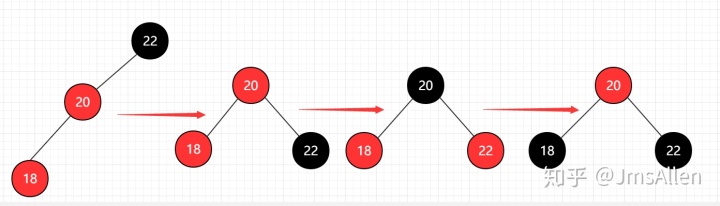
上面是在黑节点左节点的左节点添加，另外一种情况是在其右边添加一个节点，这种情况是最复杂的：

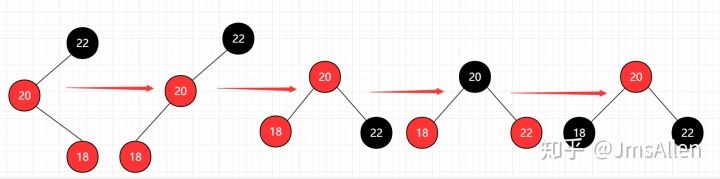
但是也不难发现，上面最后一种情况虽然复杂，但也囊括了其它所有情况

因此，最后给出完整代码以及辅助函数代码：

• 颜色翻转方法flipColors(Node<K, V> node)

// 颜色翻转
private void flipColors(Node<K, V> node) {node.color = RED;node.left.color = BLACK;node.right.color = BLACK;
}

• 左旋转方法Node<K, V> leftRotate(Node<K, V> node)

private Node<K, V> leftRotate(Node<K, V> node) {Node<K, V> x = node.right;node.right = x.left;x.left = node;x.color = node.color;node.color = RED;return x;
}

• 右旋转方法Node<K, V> rightRotate(Node<K, V> node)

private Node<K, V> rightRotate(Node<K, V> node) {Node<K, V> x = node.left;Node<K, V> temp = x.right;x.right = node;node.left = temp;x.color = node.color;node.color = RED;return x;
}

• 完整add()方法

@Override
public void add(K key, V value) {root = add(root, key, value);// 保持根节点为黑色root.color = BLACK;
}private Node<K, V> add(Node<K, V> node, K key, V value) {if (node == null) {size++;return new Node<>(key, value);}if (key.compareTo(node.key) < 0) {node.left = add(node.left, key, value);} else if (key.compareTo(node.key) > 0) {node.right = add(node.right, key, value);} else {// 如果插入节点存在，此处定义为改变 Value 的值（也可以根据情况不做改变）node.value = value;}if (isRed(node.right) && !isRed(node.left)) {node = leftRotate(node);}if (isRed(node.left) && isRed(node.left.left)) {node = rightRotate(node);}if (isRed(node.left) && isRed(node.right)) {flipColors(node);}return node;
}