专业手机网站建设设计/软文推广媒体

点击上方蓝色字体“高中数学王晖”关注王晖老师，免费获取各种知识干货和学习经验~~~您的点赞转发是对老师的最大鼓舞~~~

距高考还有262天

1

三角函数有界性

在三角函数中，正弦函数与余弦函数具有一个最基本也是最重要的特征——有界性，这是求解三角最值问题的最常用的方法。另外，在解三角形问题中，两大利器就是正弦定理和余弦定理，它们两个的基本操作方法无非就是“角化边”或者“边化角”，将多元问题降元，转变成一元问题，再结合三角函数的有界性即可求解出最值。

1利用y=Asin(wx+Ψ)求解

例题1：在△ABC中，a，b，c分别为内角A，B，C所对的边，若a=√3，A=π/3，试求b+c的最大值。

例题2：已知△ABC为等腰直角三角形，D为△ABC外一点，DB=2，DC=1，具体如下图所示，求平面四边形ABDC面积的最大值。

变式1：在△ABC中，A，B，C的对边分别是a，b，c，已知bcosC+√3bsinC-a-c=0(1)求B；(2)若b=√3，求2a+c的取值范围变式2：在△ABC中，a²+c²=b²+√2ac，(1)求B的大小；(2)求√2cosA+cosC的最大值。

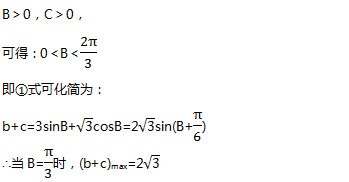
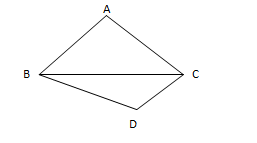
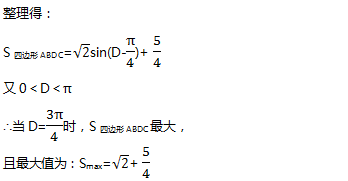
2换元为二次函数求解

例题：在△ABC中，A，B，C的对边分别是a，b，c，且a=btanA，且B为钝角。(1)证明：B-A=π/2(2)求sinA+sinC的取值范围

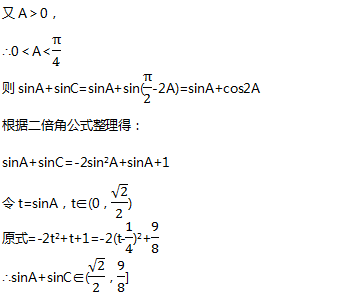
3利用函数单调性求解

例题：在锐角△ABC中，若b=2，B=2A，则试求c的取值范围。

2

二次函数性质

将求解的最值问题转换成二次函数的最值问题，这样题目就迎刃而解。

例题：已知△ABC中，c=2，b=√3a，则试求△ABC面积的最大值。

3

基本不等式及推论

利用正弦定理或余弦定理，转化为二元问题，再利用基本不等式及其推论求解最值。例题1：在△ABC中，A，B，C的对边分别是a，b，c，已知cosC+(cosA-√3sinA)cosB=0。(1)求B的大小(2)若a+c=1，求b的取值范围

例题2：在△ABC中，A，B，C的对边分别是a，b，c，已知a+b=2c，求cosC的最小值。

变式1：在△ABC中，A，B，C的对边分别是a，b，c，已知a=bcosC+csinB

(1)求B的值；

(2)若b=2时，求△ABC面积的最大值。

变式2：在△ABC中，A，B，C的对边分别是a，b，c，已知cosC是方程2x²-3x-2=0的一个根。

(1)求C的大小；

(2)当a+b=10时，求△ABC周长的最小值。

4

阿波罗尼斯圆

基本概念：

一般地，平面内到两定点A,B距离之比为常数λ(λ≠1)的点P的轨迹为圆，此圆称为阿波罗尼斯圆。

阿波罗尼斯圆的证明：平面内有一动点P，又A，B为两个定点，且有PA=λPB，试求点P的轨迹方程。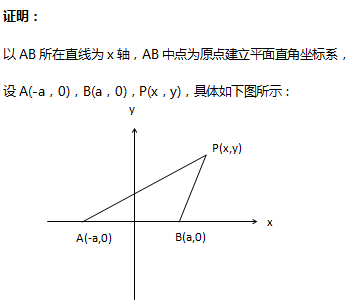

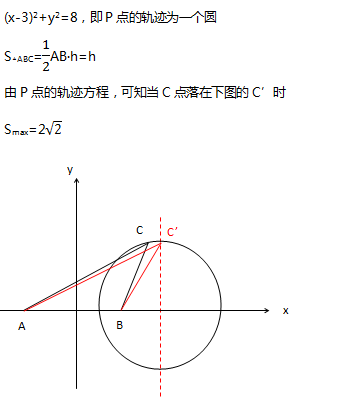
例题：在△ABC中，AB=2，AC=√2BC，求△ABC面积最大值。

变式：在△ABC中，AB=AC，点D是AC的中点，且BD=2，试求△ABC面积的最大值。往期优质数学干货链接：

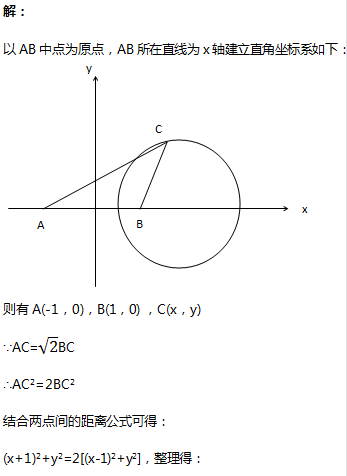
【鸢飞鱼跃】高中数学各类题型"涨分秘籍"&"答题技巧"------你值得拥有！！！

【条脩叶贯】优化解几运算的十种方法------教你精准、快速、高效答题！！！

【柳暗花明】函数零点问题的超全汇总------真的是“涨”知识了！！！

【时不我待】是时候和三角形的“四心”做个了结了！！！

【谦恭仁厚】"三角函数"&"解三角形"最值问题全梳理------各类题型齐聚一堂！！！