北京网络公司网站/企业推广网
题目地址:
https://www.luogu.com.cn/problem/P5020
题目描述:
在网友的国度中共有nnn种不同面额的货币,第iii种货币的面额为a[i]a[i]a[i],你可以假设每一种货币都有无穷多张。为了方便,我们把货币种数为nnn、面额数组为a[1..n]a[1..n]a[1..n]的货币系统记作(n,a)(n,a)(n,a)。在一个完善的货币系统中,每一个非负整数的金额xxx都应该可以被表示出,即对每一个非负整数xxx,都存在nnn个非负整数t[i]t[i]t[i]满足a[i]×t[i]a[i] \times t[i]a[i]×t[i]的和为xxx。然而, 在网友的国度中,货币系统可能是不完善的,即可能存在金额xxx不能被该货币系统表示出。例如在货币系统n=3,a=[2,5,9]n=3, a=[2,5,9]n=3,a=[2,5,9]中,金额1,31,31,3就无法被表示出来。 两个货币系统(n,a)(n,a)(n,a)和(m,b)(m,b)(m,b)是等价的,当且仅当对于任意非负整数xxx,它要么均可以被两个货币系统表出,要么不能被其中任何一个表出。 现在网友们打算简化一下货币系统。他们希望找到一个货币系统(m,b)(m,b)(m,b),满足(m,b)(m,b)(m,b)与原来的货币系统(n,a)(n,a)(n,a)等价,且mmm尽可能的小。他们希望你来协助完成这个艰巨的任务:找到最小的mmm。
输入格式:
输入文件的第一行包含一个整数TTT,表示数据的组数。
接下来按照如下格式分别给出TTT组数据。 每组数据的第一行包含一个正整数nnn。接下来一行包含nnn个由空格隔开的正整数a[i]a[i]a[i]。
输出格式:
输出文件共有TTT行,对于每组数据,输出一行一个正整数,表示所有与(n,a)(n,a)(n,a)等价的货币系统(m,b)(m,b)(m,b)中,最小的mmm。
数据范围:
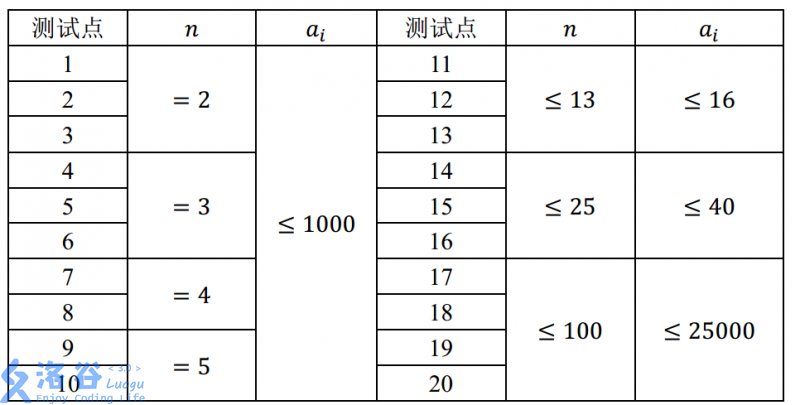
对于100%100\%100%的数据,满足1≤T≤20,n,a[i]≥11 ≤ T ≤ 20, n,a[i] ≥ 11≤T≤20,n,a[i]≥1。
思路参考https://blog.csdn.net/qq_46105170/article/details/114298230。代码如下:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;const int N = 110, M = 25010;
int n, a[N];
bool f[M];int main() {int T;scanf("%d", &T);while (T--) {scanf("%d", &n);for (int i = 1; i <= n; i++) scanf("%d", &a[i]);sort(a + 1, a + 1 + n);memset(f, 0, sizeof f);f[0] = true;int res = 0;for (int i = 1; i <= n; i++) {if (!f[a[i]]) res++;// 看看新增一种货币a[i]能使得哪些数量得以表示for (int j = 0; j <= a[n] - a[i]; j++)f[j + a[i]] |= f[j];}printf("%d\n", res);}
}
每组数据时间复杂度O(nmaxiai)O(n\max_i a_i)O(nmaxiai),空间O(maxiai)O(\max_i a_i)O(maxiai)。
