北京东八区网站建设/2024年3月份病毒会爆发吗

1. 有效的括号

OJ：有效的括号

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

（1）左括号必须用相同类型的右括号闭合。

（2）左括号必须以正确的顺序闭合。

（3）每个右括号都有一个对应的相同类型的左括号。

示例 1：

输入：s = "()"

输出：true

示例 2：

输入：s = "()[]{}"

输出：true

示例 3：

输入：s = "(]"

输出：false

解题思路

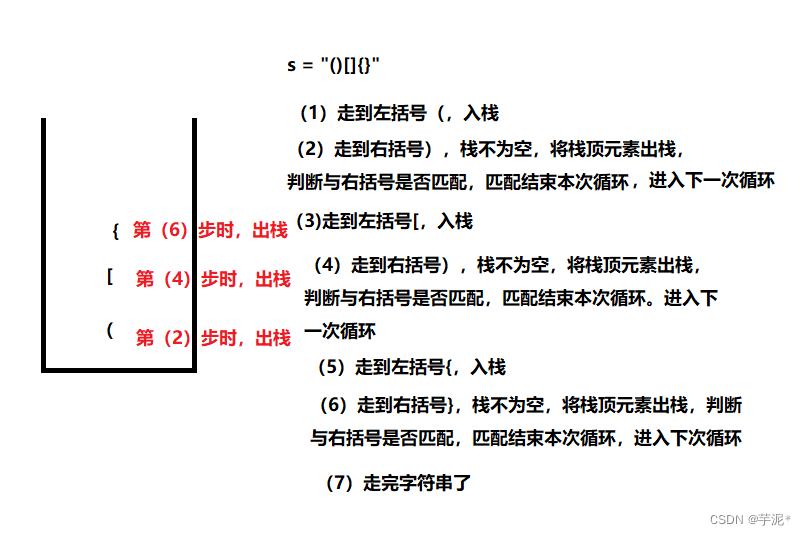
（1）左括号，直接入栈

（2）右括号，与栈顶的左括号进行匹配，如果不匹配直接返回false；否则继续循环

 循环结束后，如果栈空则匹配，否则左括号比右括号多肯定不匹配

public boolean isValid(String s) {Stack<Character> stack = new Stack<>();for (int i = 0; i < s.length(); i++) {char c = s.charAt(i);if (c == '[' || c == '{' || c == '('){stack.push(c);}else {if (stack.isEmpty()){return false;}char temp = stack.peek();if (c == '}' && temp == '{'){stack.pop();continue;}if (c == ']' && temp == '['){stack.pop();continue;}if (c == ')' && temp == '('){stack.pop();continue;}return false;}}return stack.isEmpty();}

2. 逆波兰表达式求值

OJ：

给你一个字符串数组 tokens ，表示一个根据 逆波兰表示法 （也叫后缀表达式：将运算符写在操作数之后）表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

示例 1：

输入：tokens = ["2","1","+","3","*"]

输出：9

解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：

输入：tokens = ["4","13","5","/","+"]

输出：6

解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

示例 3：

输入：tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]

输出：22

解释：该算式转化为常见的中缀算术表达式为：

   ((10 * (6 / ((9 + 3) * -11))) + 17) + 5

= ((10 * (6 / (12 * -11))) + 17) + 5

= ((10 * (6 / -132)) + 17) + 5

= ((10 * 0) + 17) + 5

= (0 + 17) + 5

= 17 + 5

= 22

解题思路

对tokens数组进行遍历，依次获取到每个元素，如果：

（1）该元素是数字(注意：不是运算符肯定是数字)，将该数字入栈

（2）该元素是运算符，从栈顶获取该运算符对应的右左操作数，进行相应的操作，最后将结果入栈

（3）循环结束后，栈顶的元素就是最终表达式的结果

public int evalRPN(String[] tokens) {Stack<Integer> s = new Stack<>();for(String e : tokens){// 如果是数字，直接入栈if(!(e.equals("+") || e.equals("-") || e.equals("*") || e.equals("/"))){s.push(Integer.valueOf(e));}else{// 说明e是个操作符// 从栈顶取两个数字作为该操作符的右左操作数，// 注意：栈是后进先出，所以先取到的是右操作数，后取到的是左操作数int right = s.pop();int left = s.pop();// 进行对应的操作，然后将结果入栈switch(e){case "+":s.push(left + right);break;case "-":s.push(left - right);break;case "*":s.push(left * right);break;case "/":s.push(left / right);break;}}}// 最终栈顶元素就是最后的结果return s.peek();}}

3. 最小栈

OJ：最小栈

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:

        MinStack() 初始化堆栈对象。

        void push(int val) 将元素val推入堆栈。

        void pop() 删除堆栈顶部的元素。

        int top() 获取堆栈顶部的元素。

        int getMin() 获取堆栈中的最小元素。

示例 1:

输入： ["MinStack","push","push","push","getMin","pop","top","getMin"]

                [[],[-2],[0],[-3],[],[],[],[]]

输出： [null,null,null,null,-3,null,0,-2]

解释： MinStack minStack = new MinStack();

            minStack.push(-2);

            minStack.push(0);

            minStack.push(-3);

            minStack.getMin(); --> 返回 -3.

            minStack.pop(); minStack.top(); --> 返回 0.

            minStack.getMin(); --> 返回 -2.

解题思路

• 思路1

（1）利用两个栈，一个为正常栈(保存所有的进出栈数据)，一个为最小栈(只有当数据为最小时，才会入栈)

（2）核心在于：入栈时，若数据最小，需要两个栈都要入栈，出栈时，如果出的数据为最小，需要更新最小栈

Stack<Integer> dataSt;  // 存放数据Stack<Integer> minSt;   // 存放最小值public MinStack() {dataSt = new Stack<>();minSt = new Stack<>();}// 入栈时：// 数据栈：每次都要压入一个元素// 最小值栈：当最小值栈为空 或者 当前插入元素小于最小值栈栈顶元素时入栈public void push(int val) {dataSt.push(val);if(minSt.isEmpty() || val <= minSt.peek()){minSt.push(val);}}// 出栈时：// 最小值栈：栈顶与数据栈栈顶元素相等时才可以出，注意使用equals比较// 数值栈每次都要出一个元素public void pop() {if(dataSt.peek().equals(minSt.peek())){minSt.pop();}dataSt.pop();}public int top() {return dataSt.peek();}public int getMin() {return minSt.peek();}

• 思路2

利用两个栈，一个正常栈s1，一个存最小栈s2，两个栈为空时，直接入栈；栈不为空时，s1正常入栈，判断入栈元素与栈s2的栈顶元素的大小，比栈顶元素小，元素入s2栈；比栈顶元素大，将栈顶元素再次入栈。
出栈时两个栈顶元素一起出栈，检查栈顶元素时，检查栈s1的，检查最小元素时，检查s2的栈顶元素。

//    保存数值Stack<Integer> s1 = new Stack<>();
//    保存最小数Stack<Integer> s2 = new Stack<>();public MinStack() {s1 = new Stack<>();s2 = new Stack<>();}public void push(int val) {s1.push(val);if (s2.isEmpty()){s2.push(val);}else {int temp = s2.peek();if (val < temp){s2.push(val);}else {s2.push(temp);}}}public void pop() {s1.pop();s2.pop();}public int top() {return s1.peek();}public int getMin() {return s2.peek();}

4. 验证栈序列

OJ：验证栈序列

给定 pushed 和 popped 两个序列，每个序列中的 值都不重复，只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时，返回 true；否则，返回 false 。

示例 1：

输入：pushed = [1,2,3,4,5], popped = [4,5,3,2,1]

输出：true

解释：我们可以按以下顺序执行： push(1), push(2), push(3), push(4), pop() -> 4, push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1

示例 2：

输入：pushed = [1,2,3,4,5], popped = [4,3,5,1,2]

输出：false

解释：1 不能在 2 之前弹出。

解题思路

入栈：当栈为空，或者栈顶元素和待出栈元素不相等时

注意：入栈时要保证有元素，如果没有元素则一定不相等

出栈：当栈顶元素待出栈元素相同时出栈

循环进行上述过程即可，直到所有的元素全部出栈

将pushed数组的元素入栈，判断栈顶元素与popped［i］是否相等，相等出栈再将i++，直到栈顶元素与popped［i］不相等，进去下一次循环。最后栈为空时，栈序列正确，不为空栈序列错误。

public boolean validateStackSequences(int[] pushed, int[] popped) {int i = 0;Stack<Integer> stack = new Stack<>();for (int val:pushed) {stack.push(val);while (!stack.isEmpty()&&stack.peek() == popped[i]){stack.pop();i++;}}return stack.isEmpty();}

5. 用队列实现栈

OJ：用队列实现栈

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

        void push(int x) 将元素 x 压入栈顶。

        int pop() 移除并返回栈顶元素。

        int top() 返回栈顶元素。

        boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

解题思路

• 思路1

借助两个队列来模拟实现栈。一个队列是辅助的，起到导元素的作用。

入栈：先将元素放入a队列中，如果b不空，将b中所有元素导入到a中。此时，刚刚入栈的元素刚好在a的队头，然后将a和b队列交换下。即：b队列队头相当于栈顶，b队列队尾相当于栈底

出栈：  直接从b中poll()即可

获取栈顶元素：直接从b中peek()即可

    private Queue<Integer> a;  // a是用来辅助导元素的private Queue<Integer> b;  // 元素全部放在b中public MyStack() {a = new LinkedList<>();b = new LinkedList<>();}public void push(int x) {// 先把元素放入a队列中a.offer(x);while(!b.isEmpty()){a.offer(b.poll());}Queue<Integer> temp = a;a = b;b = temp;}public int pop() {return b.poll();}public int top() {return b.peek();}public boolean empty() {return b.isEmpty();}

• 思路2

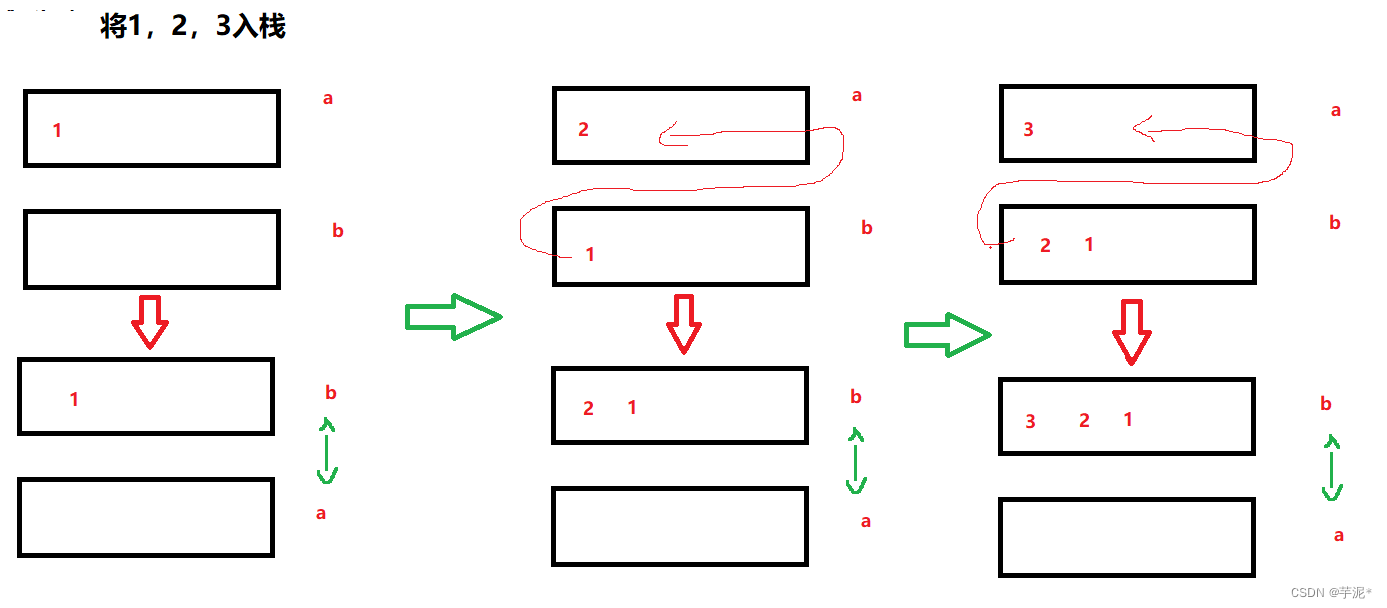
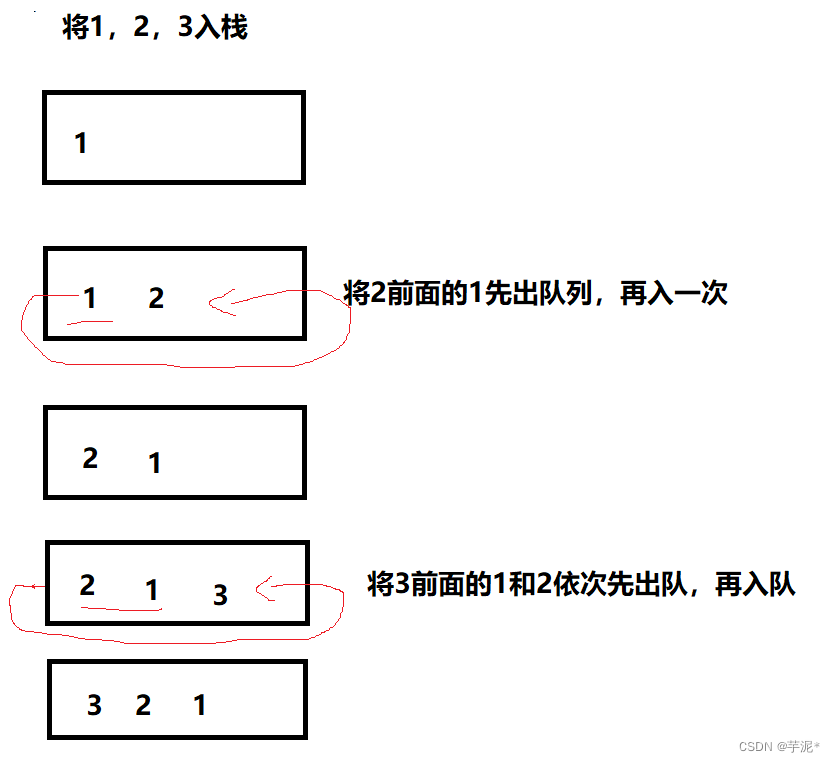
先将元素放入队列中，再将元素前面的所有元素依次入队

    Queue<Integer> queue = new LinkedList<>();public MyStack() {}public void push(int x) {if (queue.isEmpty()){queue.offer(x);return;}int size = queue.size();queue.offer(x);while (size != 0){queue.offer(queue.poll());size--;}}public int pop() {return queue.poll();}public int top() {return queue.peek();}public boolean empty() {return queue.isEmpty();}

6. 用栈实现队列

OJ：用栈实现队列

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

        void push(int x) 将元素 x 推到队列的末尾

        int pop() 从队列的开头移除并返回元素

        int peek() 返回队列开头的元素

        boolean empty() 如果队列为空，返回 true ；否则，返回 false

解题思路

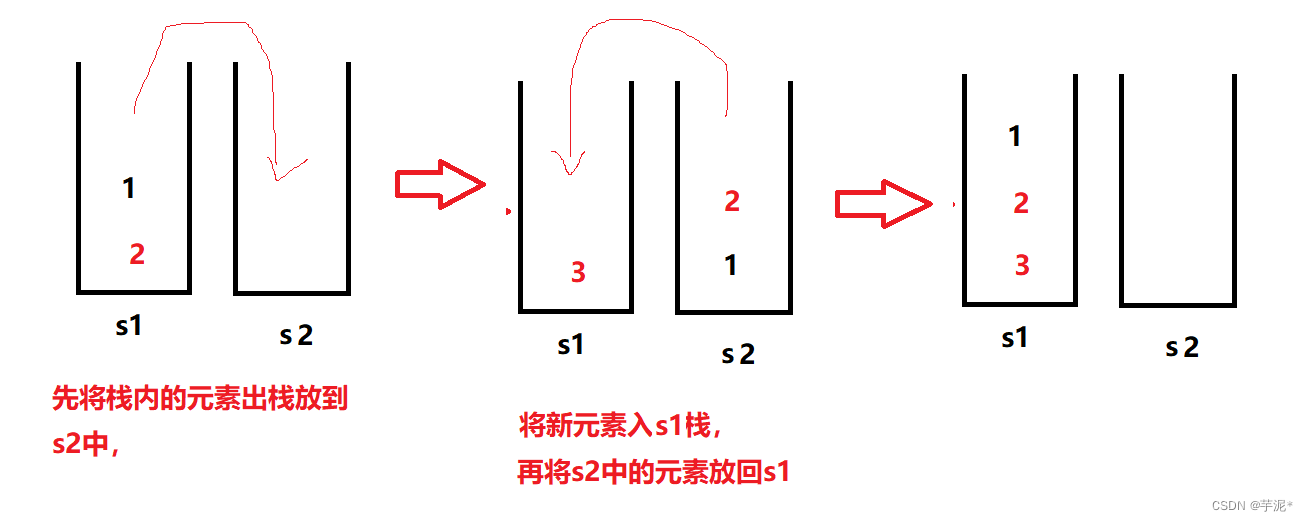
利用两个栈模拟实现队列

s2作为辅助栈，s1作为真正存储的栈。

    Stack<Integer> s1 = new Stack<>();Stack<Integer> s2 = new Stack<>();public MyQueue() {}public void push(int x) {while (!s1.isEmpty()){s2.push(s1.pop());}s1.push(x);while (!s2.isEmpty()){s1.push(s2.pop());}}public int pop() {return s1.pop();}public int peek() {return s1.peek();}public boolean empty() {return s1.isEmpty();}

7. 设计循环队列

 OJ：设计循环队列

设计你的循环队列实现。 循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。

循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。

你的实现应该支持如下操作：

        MyCircularQueue(k): 构造器，设置队列长度为 k 。

        Front: 从队首获取元素。如果队列为空，返回 -1 。

        Rear: 获取队尾元素。如果队列为空，返回 -1 。

        enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。

        deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。

        isEmpty(): 检查循环队列是否为空。

        isFull(): 检查循环队列是否已满。

解题思路

参考这一篇：循环队列

    private int head;private int tail;private int size;int data[];public MyCircularQueue(int k) {data = new int[k + 1];head = tail = 0;}public boolean enQueue(int value) {if(isFull()){return false;}data[tail] = value;tail = (tail + 1) % data.length;size ++;return true;}public boolean deQueue() {if(isEmpty()){return false;}head = (head + 1) % data.length;size --;return true;}public int Front() {if(isEmpty()){return -1;}return data[head];}public int Rear() {if(isEmpty()){return -1;}return data[(tail - 1 + data.length) % data.length];}public boolean isEmpty() {return size == 0;}public boolean isFull() {return size == data.length - 1;}