珠海高端网站建设/百度一下网页打开
参考视频:MIT微积分
如何得到的自然对数 lnlnln
-
首先我们知道以 eee 为底的指数函数 exe^xex
-
其次,我们引入反函数(逆函数)的概念 f−1(y)f^{-1}(y)f−1(y)
对于任意的 xxx 如果 f(x)=yf(x)=yf(x)=y 那么 x=f−1(x)x=f^{-1}(x)x=f−1(x)
-
举个例子来说:
y=ax+b→f(x)=y=ax+by=ax+b \rightarrow f(x)=y=ax+by=ax+b→f(x)=y=ax+b
x=y−ba=f−1(y)x=\frac{y-b}{a}=f^{-1}(y)x=ay−b=f−1(y)
- 因此我们定义 y=exy=e^xy=ex 的反函数是 f−1(y)=lnyf^{-1}(y)=lnyf−1(y)=lny 即 ln(ex)=xln(e^x)=xln(ex)=x
lnlnln 函数的导数
- 因为我们现在知道 lnlnln 是 exe^xex 的反函数,我们尝试对他进行求导
- 首先 ln(ex)=xln(e^x)=xln(ex)=x 两边同时求导:左边根据链式法则
d(lny)dy⋅dydx=1\frac{d(lny)}{dy}\cdot \frac{dy}{dx}=1dyd(lny)⋅dxdy=1
d(lny)dy⋅dexdx=1\frac{d(lny)}{dy}\cdot \frac{de^x}{dx}=1dyd(lny)⋅dxdex=1
d(lny)dy⋅ex=1\frac{d(lny)}{dy}\cdot e^x=1dyd(lny)⋅ex=1
d(lny)dy⋅=1ex\frac{d(lny)}{dy}\cdot =\frac{1}{e^x}dyd(lny)⋅=ex1 - 关键来了,因为现在我们的反函数的主题是 yyy,也就是 f−1(y)f^{-1}(y)f−1(y) 我们关心的是 yyy,所以在上述式子中需要把 exe^xex 替换成 yyy,所以可以得到:
d(lny)dy⋅=1y\frac{d(lny)}{dy}\cdot =\frac{1}{y}dyd(lny)⋅=y1
arcsinarcsinarcsin 的导数
-
我们知道 arcsinarcsinarcsin 是 sinsinsin 的反函数,即 y=sin(x),sin−1(y)=xy=sin(x), sin^{-1}(y)=xy=sin(x),sin−1(y)=x
-
为了方便观察,我们暂且把这个 sinsinsin 的反函数写成 A(y)A(y)A(y),所以 A(y)=A(sin(x))=xA(y)=A(sin(x))=xA(y)=A(sin(x))=x
-
两边同时求导:(左边还是根据链式法则)
dA(y)dy⋅dydx=1\frac{dA(y)}{dy}\cdot \frac{dy}{dx}=1dydA(y)⋅dxdy=1
dA(y)dy⋅dsin(x)dx=1\frac{dA(y)}{dy}\cdot \frac{dsin(x)}{dx}=1dydA(y)⋅dxdsin(x)=1
dA(y)dy⋅cos(x)=1\frac{dA(y)}{dy}\cdot cos(x)=1dydA(y)⋅cos(x)=1 -
这时候要把 cos(x)cos(x)cos(x) 化成使用 yyy 表示的形式
-
又因为 y=sin(x)y=sin(x)y=sin(x) 我们知道 sin2(x)+cos2(x)=1sin^2(x)+cos^2(x)=1sin2(x)+cos2(x)=1 所以 cos(x)=1−sin2(x)cos(x)=\sqrt{1-sin^2(x)}cos(x)=1−sin2(x)
-
所以:
dA(y)dy=11−sin2(x)=11−y2\frac{dA(y)}{dy}=\frac{1}{\sqrt{1-sin^2(x)}}=\frac{1}{1-y^2}dydA(y)=1−sin2(x)1=1−y21 -
也就是 sin−1(y)sin^{-1}(y)sin−1(y) 的导数是 11−y2\frac{1}{\sqrt{1-y^2}}1−y21
arccos 的导数
-
与上面的步骤完全一样 arccosarccosarccos 是 coscoscos 的反函数,即 y=cos(x),cos−1(y)=xy=cos(x), cos^{-1}(y)=xy=cos(x),cos−1(y)=x
-
我们暂且把这个 coscoscos 的反函数写成 A(y)A(y)A(y),所以 A(y)=A(cos(x))=xA(y)=A(cos(x))=xA(y)=A(cos(x))=x
-
两边同时求导:(左边还是根据链式法则)
dA(y)dy⋅dydx=1\frac{dA(y)}{dy}\cdot \frac{dy}{dx}=1dydA(y)⋅dxdy=1
dA(y)dy⋅dcos(x)dx=1\frac{dA(y)}{dy}\cdot \frac{dcos(x)}{dx}=1dydA(y)⋅dxdcos(x)=1
dA(y)dy⋅−sin(x)=1\frac{dA(y)}{dy}\cdot -sin(x)=1dydA(y)⋅−sin(x)=1 -
sin2(x)+cos2(x)=1sin^2(x)+cos^2(x)=1sin2(x)+cos2(x)=1 所以 −sin(x)=−1−cos2(x)-sin(x)=-\sqrt{1-cos^2(x)}−sin(x)=−1−cos2(x)
-
所以:
dA(y)dy=−11−cos2(x)=−11−y2\frac{dA(y)}{dy}=\frac{-1}{\sqrt{1-cos^2(x)}}=\frac{-1}{\sqrt{1-y^2}}dydA(y)=1−cos2(x)−1=1−y2−1 -
因此 cos−1(y)cos^{-1}(y)cos−1(y) 的导数为:−11−y2\frac{-1}{\sqrt{1-y^2}}1−y2−1
有趣的现象
- 有没有发现 (arcsin(y))′=11−y2(arcsin(y))^{'}=\frac{1}{\sqrt{1-y^2}}(arcsin(y))′=1−y21,(arccos(y))′=−11−y2(arccos(y))^{'}=\frac{-1}{\sqrt{1-y^2}}(arccos(y))′=1−y2−1 这两个加起来结果是 000
(arccos(y))′+(arcsin(y))′=0(arccos(y))^{'}+(arcsin(y))^{'}=0(arccos(y))′+(arcsin(y))′=0
- 也就是
(arccos(y)+arcsin(y))′=0(arccos(y)+arcsin(y))^{'}=0(arccos(y)+arcsin(y))′=0 - 所以肯定 arccos(y)+arcsin(y))=Carccos(y)+arcsin(y))=Carccos(y)+arcsin(y))=C 其中 CCC 是常数
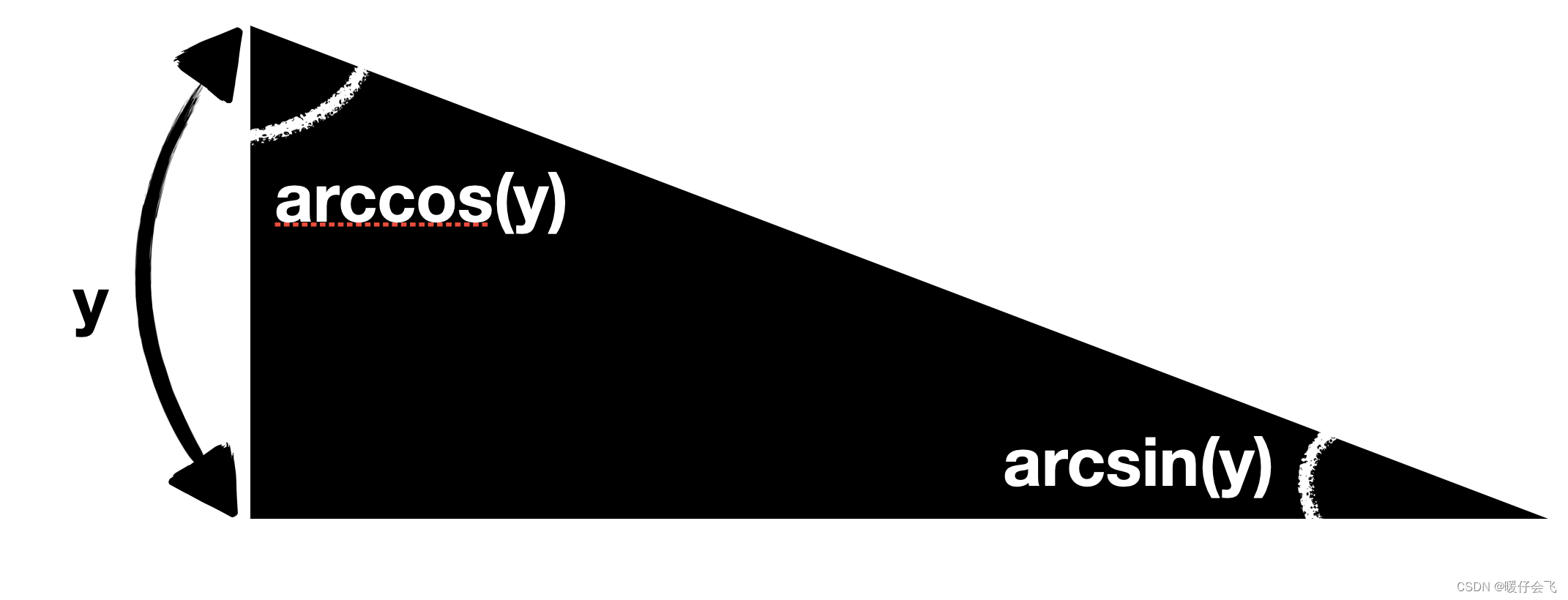
- 事实上,如上图所示,arcsinarcsinarcsin 和 arccosarccosarccos 对应的两个角之和为 π2\frac{\pi}{2}2π 确实为常数!
