室内设计网站参考/互联网优化是什么意思
PageRank是谷歌的成名之作,谷歌采用PageRank算法优化自家的搜索引擎,极大提升了搜索体验。PageRank的思想在之后也被其他各种算法借鉴和延续:比如关键词抽取算法中的textRank就借鉴了PageRank 算法的思想。接下来笔者就来简单的介绍一下此算法的主要思想。这里我用一句不是特别严谨的话点出此算法的精髓:
越是重要的网页:(1)一般会被更多的网页引用,(2)一般会被更重要的网页引用
这和学术文章一样,比如google在2018年发表的划时代意义的论文bert 估计现在citation 数量直接上到了4千多了,那很多同时发表的文章citation 数量 只有几十甚至个位数。

通过 citation 数量就可以判断一篇文章的重要性,同理通过一个网页的被引用量也可以看出此网页的重要程度,同时如果一个网页被某一个重要的网页引用了那也可以反映出此网页的分量较重。下面我们我们来看看这个思想是如何通过公式体现出来的。
PageRank公式如下
对于一个页面A,那么它的PR值为:
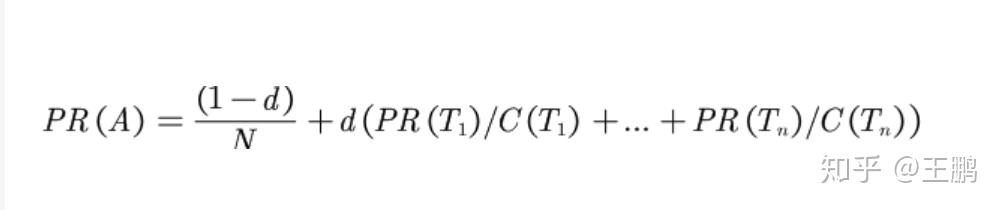
- 其中 PR(A) 是页面(节点)A的PR值 ,
- PR(Ti)是页面(节点)Ti的PR值,Ti值A页面(节点)指向的节点(即引用了A的节点),
- C(Ti)是页面(节点)Ti的出度,也就是Ti指向其他页面(节点)的边的个数,
- d 为阻尼系数,其意义是,在任意时刻,用户到达某页面(节点)后并继续向后浏览的概率。
从公式的后半部分,我们发现如果:
1.引用A页面的页面越多,
2.引用A页面的被引用量越大,
则PR(Ti)/ C(Ti)的加和就越大,A的PR值就越高。这就从公式的角度表达出来PageRank算法的思想。
PageRank公式的概率转移版本(迭代过程)
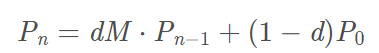
其中Pn 为第n步的PR值,d 为阻尼系数,M 为转移矩阵,P0为初始PR值: 1/页面(节点)个数。
上方两个公式其实表示同一个含义,只不过下方是程序实现过程中采用的迭代过程。
纯python实现PageRank算法
过程分为两步:
- 通过已存在的有向图构建转移矩阵M。
- 设置各节点PR的初始值(一般初始认为各节点的PR值一样,PR的初始值 = 1/节点个数),然后采用下方公式不断迭代,直到收敛。
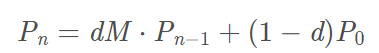
import numpy as np
def nodes2matrix(node_json):
"""
构建图的
"""node2id = {}dim = len(node_json)for id_ , key in enumerate(node_json.keys()):node2id[key] = id_ matrix = np.zeros((dim,dim))for key in node_json.keys():nodeid = node2id[key]for neighbor in node_json[key]:neighborid = node2id[neighbor]matrix[neighborid][nodeid] = 1for i in range(dim):matrix[:,i] = matrix[:,i]/sum(matrix[:,i])return matrixdef pagerank(matrix, iter_ = 10, d=0.85):length = len(matrix[0])inital_value = np.ones(length)/lengthpagerank_value = inital_valuefor i in range(10):pagerank_value = matrix@pagerank_value* d + (1-d)/lengthprint("iter {}: the pr value is {}".format(i, pagerank_value))return pagerank_value给程序输入一个 {"A":["B","C"], "B":["A","C"], "C":["D","B"], "D":["A","B"} JSON 类型保存的图,然后采用PageRank算法对每个节点的pr值进行计算,代码如下:
node_json = {"A":["B","C"], "B":["A","C"], "C":["D","B"], "D":["A","B"}
matrix = nodes2matrix(node_json)
print("the matrix is :",matrix)
pagerank(matrix)###程序输出
the matrix is : [[0. 0.5 0. 0.5][0.5 0. 0.5 0.5][0.5 0.5 0. 0. ][0. 0. 0.5 0. ]]iter 0: the pr value is [0.25 0.35625 0.25 0.14375]iter 1: the pr value is [0.25 0.31109375 0.29515625 0.14375 ]iter 2: the pr value is [0.23080859 0.33028516 0.27596484 0.16294141]iter 3: the pr value is [0.24712129 0.32212881 0.27596484 0.15478506]iter 4: the pr value is [0.24018839 0.32559526 0.27943129 0.15478506]iter 5: the pr value is [0.24166163 0.32412202 0.27795805 0.1562583 ]iter 6: the pr value is [0.24166163 0.32474814 0.27795805 0.15563217]iter 7: the pr value is [0.24166163 0.32448204 0.27822416 0.15563217]iter 8: the pr value is [0.24154854 0.32459513 0.27811106 0.15574527]iter 9: the pr value is [0.24164467 0.32454707 0.27811106 0.1556972 ]pagerank value is : {'A': 0.2416446697182898, 'B': 0.32454706832136704, 'C': 0.2781110610248022, 'D': 0.15569720093554096}结果如上:其中B的pr值最高,约为0.32, 从我输入给算法的图可以看出:A,C,D 网页(节点)都链接到了B网页(节点),从这点我们也可以看出,算法的结果非常不错。
调用networkx中的pagerank 算法包
采用networkx内置的pagerank算法,并构建相同的有向图,将阻尼系数(networkx中的参数数是alpha)设置成0.85, 代码如下:
import networkx as nx# 创建有向图
G = nx.DiGraph()
# 有向图之间边的关系
edges = [("A", "B"), ("A", "C"), ("B", "A"), ("B", "C"), ("C", "D"),("C", "B"), ("D", "B"), ("D", "A")]
for edge in edges:G.add_edge(edge[0], edge[1])
pagerank_list = nx.pagerank(G, alpha=0.85)
print("pagerank 值是:", pagerank_list)###程序输出
pagerank 值是: {'A': 0.24161249618205796, 'B': 0.3245609358176832, 'C': 0.27812437505969145, 'D': 0.15570219294056742}结果如上,最终结果和上方基本一样,networkx 中使用实现的pagerank就是笔者用纯python的实现过程。
结语
PageRank算法的思想其实在社会中也可以经常别察觉,比如一个人如果有很多特别有名望的人给他写推荐信,那证明此人是个优秀的人;一本书如果有很多业界的大佬为它写序,那证明此书是本值得看的书。发现没,算法有时候和生活真的息息相关。
