广东省建设厅证书查询官网/seo和sem的概念

树，是一种重要的数据结构。

很多的数据结构都是树的发散。包括后面的动态规划，图论，排序。

在做题过程中，树这部分主要分为二叉树（包括完全二叉树）和二叉搜索树。这里我们分成两部分来概括。

二叉树部分有这几篇：

1. **关于二叉树的递归解法
2. 递归与回溯在二叉树中的应用
3. 二叉树的构造
4. 关于层序遍历（BST）

遍历

关于二叉树的遍历，大体上可以分为深度优先搜索和广度优先搜索。

具体看这篇文章：

二叉树的遍历

这里我们就在掌握了基本遍历方法的基础上，再来看这些题目。

递归和迭代

对于常见的前序遍历、中序遍历和后序遍历，可以用递归法写也可以用迭代法来写。

而对于广度优先的层序遍历来说，基本都是用迭代法。

我们本着优先掌握一种方法的前提下，对这类题目大致分为递归和迭代两类。

（建议做完题目后看这小节内容更深刻）

递归

在使用递归的题目中，有些题目是需要单独的**辅助函数（或者说遍历函数）**来解决问题。而有些题目是可以根据递归函数的定义在主函数中直接完成的。

这也与要求的函数是否能传入你需要的参数有关。

这两种解法非常的玄妙，有时候还可以共存，这就需要多做题来摸索这种规律。

前序遍历和后序遍历

我们也会发现有时候使用前序和后序遍历好像没什么区别。这就说明我们的节点操作代码对于位置没什么要求。

所以这部分题目会把操作代码写到前序的位置，但并不意味着一定要用前序。

而前序和后序的真正区别是什么呢？

前序遍历是从节点出发的，而后序遍历是从叶子节点出发的。

这就说明前序遍历不能得知子树的信息，而后序遍历可以。

这是真正使用后序遍历的原因，务必多多体会。

主递归的题目

递归的题目比较跳跃，不像迭代大部分用在层序遍历。

递归还有一点很重要的理解：

把递归函数想成帮你解决问题的函数，直接使用返回的值而不是去深入到递归中去。

下面就先来盘点递归中的经典题目。

二叉树的深度

深度的题目分为最大和最小。

leetcode 104 二叉树的最大深度

二叉树的最大深度是从根节点到最远叶子节点最长路径的节点数。

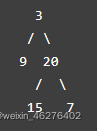
比如这棵树的最大深度就是3

我们直接说一体的递归解法。想要知道根节点这棵树的最大深度，可以先知道左右子树的最大深度。

根节点这棵树的最大深度就是左右子树最大深度的最大值再加上根节点。（哪个更深选哪个）

int maxDepth(TreeNode* root) {if(root==NULL)return 0;int left=maxDepth(root->left);int right=maxDepth(root->right);return max(left,right)+1;}

继续延伸为n叉树。

leetcode 559 n叉树的最大深度

n叉树只是需要取所有子树的最大深度中的最大值，比二叉树多了几个支而已。

int maxDepth(Node* root) {if(root==NULL)return 0;int depth=0;for(int i=0;i<root->children.size();i++){depth=max(depth,maxDepth(root->children[i]));}return depth+1;}

这里把求depth的过程合并了，直接找最大的即可。

再来看最小深度。

leetcode 111 二叉树的最小深度

最小深度并不是返回min(left,right)+1这么简单。

如果一棵二叉树只有右子树没有左子树，那么按照我们这种求法，最小深度的当然是左子树+1（因为是空）

但这很明显是错误的，因为最小深度的叶子节点必须是左右都为空，所以需要改进一部分。

int minDepth(TreeNode* root) {if(root==NULL)return 0;int left=minDepth(root->left);int right=minDepth(root->right);if(root->left==NULL&&root->right!=NULL){return right+1;}if(root->right==NULL&&root->left!=NULL){return left+1;}return min(left,right)+1;}

单独判断左子树为空和右子树为空的情况。

左子树为空那就返回右子树的最小深度，右子树同理。

二叉树的直径

leetcode 543 二叉树的直径

这也是一道和深度有关的题目。

直径就是任意两个节点的路径长度的最大值。

比如这棵树，直径为3，[4-2-1-3]或者[5-2-1-3]都是答案。

这和深度有什么关系呢？

仔细分析就会发现，直径就是左右子树的最大深度和

也就是在求最大深度的基础上，把左右子树的最大深度相加即可。

因为需要返回的是直径，而我们需要求最大深度，所以需要一个辅助函数来求最大深度，同时帮我们计算直径。

int maxDepth(TreeNode *root){if(root==NULL)return 0;int left=maxDepth(root->left);int right=maxDepth(root->right);int depth=left+right;diameter=max(depth,diameter);//直径return max(left,right)+1;}

依旧是求最大深度的方式，只是多一个直径的计算。

最后在主函数中返回直径。

int diameterOfBinaryTree(TreeNode* root) {maxDepth(root);return diameter;}

翻转二叉树

在二叉树中，还有很多题目是对树本身进行处理，比如反转、对折、拉伸等等。

我们先来看一道简单的翻转。

leetcode 226 翻转二叉树

将一棵二叉树翻转，可以先翻转根节点，再翻转子树。也可以反过来。

这就说明可以前序也可以后序（但是不能中序）

这里我们选择后序，交换左右子树。

TreeNode* invertTree(TreeNode* root) {if(root==NULL)return 0;TreeNode *left=invertTree(root->left);TreeNode *right=invertTree(root->right);root->left=right;root->right=left;return root;}

相同的二叉树

leetcode 100 相同的树

判断两棵二叉树是否相同。

从递归的思路出发，我们可以从子树开始，先判断是否相同，也就是后序遍历。

在进入递归之前，可以对特殊情况进行一些过滤。

bool isSameTree(TreeNode* p, TreeNode* q) {if(p==NULL&&q==NULL){return true;}else if(p==NULL&&q!=NULL){return false;}else if(p!=NULL&&q==NULL){return false;}else if(p->val!=q->val){return false;}return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);}

这里后序遍历可能看不太出来，其实分解最后的return，相当于先递归再做操作。

对称二叉树

leetcode 101 对称二叉树

检查一棵二叉树是否轴对称

与上一题只有一点点区别。

还是从递归的思路出发，我们可以从子树开始，先判断是否对称，也就是后序遍历

但在进入递归之前，可以对特殊情况进行一些过滤。

而且我们要比较的左孩子节点的右子树和右孩子节点的左子树（对称），所以需要两个参数，于是构建辅助函数。

bool compare(TreeNode* left,TreeNode* right){if(left==NULL&&right==NULL){return true;}else if(left==NULL&&right!=NULL){return false;}else if(left!=NULL&&right==NULL){return false;}else if(left->val!=right->val){return false;}return compare(left->right,right->left)&&compare(left->left,right->right);}

只有左子树根节点等于右子树根节点时才进行比较。

注意为空时也算对称。

主函数：

bool isSymmetric(TreeNode* root) {if(root==NULL)return true;return compare(root->left,root->right);}

完全二叉树的节点个数

leetcode 222 完全二叉树的节点个数

给一棵完全二叉树，求出该树的节点个数。

我们先从普通二叉树的角度出发，不考虑完全二叉树的特性。

就一棵普通二叉树的节点个数。

这时可以从左右子树出发，先求出左右子树的节点个数，再回到根节点，也就是后序遍历。

非常简单，甚至没有多余的逻辑。

int countNodes(TreeNode* root) {if(root==NULL)return 0;int left=countNodes(root->left);int right=countNodes(root->right);return left+right+1;}

当然，如果这道题让你用完全二叉树的性质来做，就不可以这样做了。

完全二叉树的最后一层叶子节点不是满的，但我们从根节点出发，一直递归左右子树，最后总会到达满二叉树的位置。

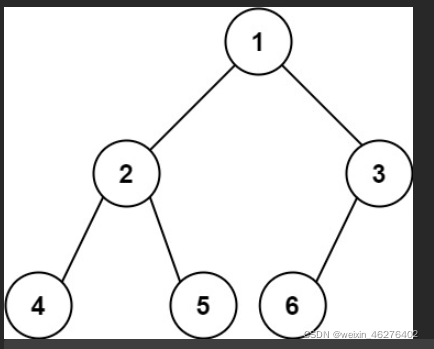
比如上面这棵完全二叉树，[2,4,5]是满二叉树，[6]本身也是满二叉树。

对于满二叉树来说可以用【2^树深度-1】来计算节点数

当左子树和右子树深度相同时，说明左子树是满二叉树

我们可以借助这个性质来递归的计算

int countNodes(TreeNode* root) {if(root==NULL)return 0;TreeNode* left=root->left;TreeNode* right=root->right;int leftHigh=0;int rightHigh=0;//求左子树深度while(left){left=left->left;leftHigh++;}//求右子树深度while(right){right=right->right;rightHigh++;}if(leftHigh==rightHigh){return (2<<leftHigh)-1;}return countNodes(root->left)+countNodes(root->right)+1;}

先判断1为根节点的树是不是满二叉树，不是就继续递归左右子树。

二叉树展开为链表

再来一道二叉树操作性的题目

leetcode 114 二叉树展开为链表

把一个二叉树展开为一个单链表。

看似将二叉树变为链表非常复杂，但在递归思维下其实很容易。

我们把flatten这个函数看作帮我们拉直二叉树的函数。

这样当flatten(root->left)和flatten(root->right)时，我们得到的就是已经变成链表的结果了，再去思考根节点如何操作即可。

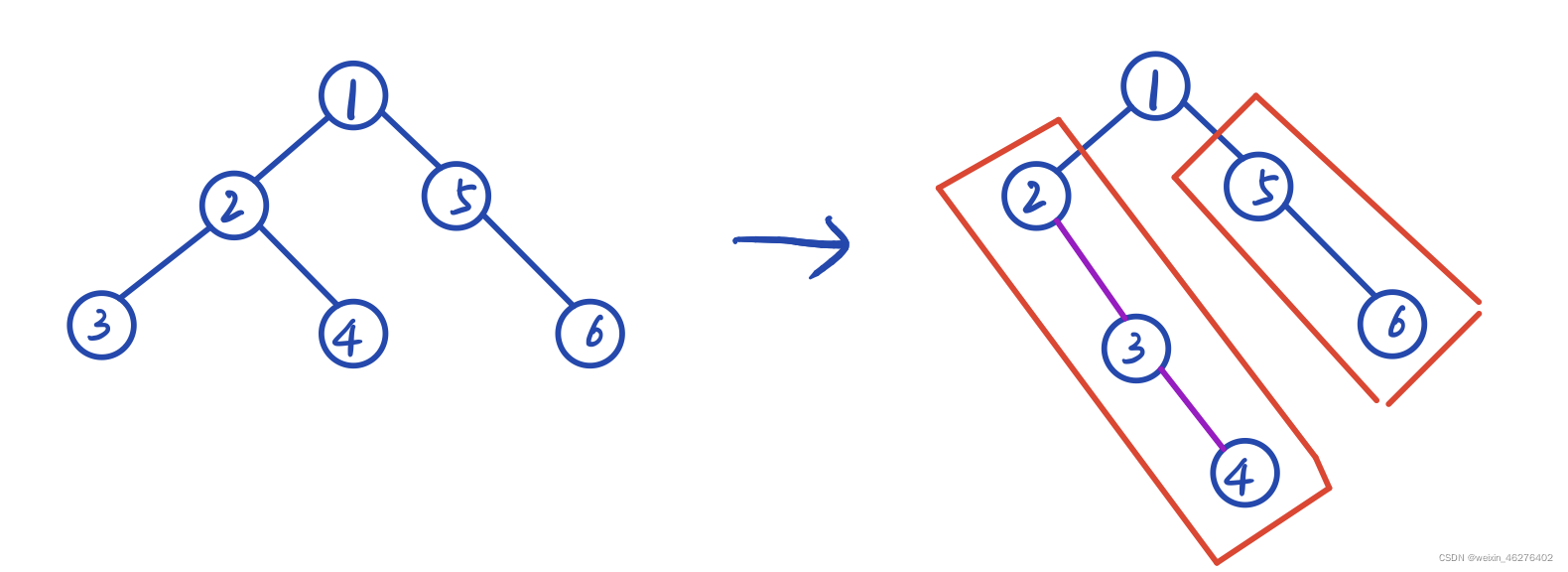
可以看到最后一步只需要把2，3，4连到1的右子树，然后把5，6连到4的后面。

void flatten(TreeNode* root) {if(root==NULL)return;flatten(root->left);flatten(root->right);TreeNode *left=root->left;TreeNode *right=root->right;//2,3,4连到1root->right=left;root->left=NULL;TreeNode* p=root;while(p->right!=NULL){p=p->right;//先找到最后一个位置}//把5，6连到4p->right=right;}

   if(root==NULL)return;flatten(root->left);flatten(root->right);TreeNode *left=root->left;TreeNode *right=root->right;//2,3,4连到1root->right=left;root->left=NULL;TreeNode* p=root;while(p->right!=NULL){p=p->right;//先找到最后一个位置}
//把5，6连到4p->right=right;}