武汉 做网站/哪些网站可以seo

第 1 章 基本介绍
1.1 研究背景
本次研究数据来源于阿里天池新人赛区工业蒸汽量预测比赛。众所周知,火力发电的基本原理是:燃料在燃烧时加热水生成蒸汽,蒸汽压力推动汽轮机旋转,然后汽轮机带动发电机旋转,产生电能。在这一系列的能量转化中,影响发电效率的核心是锅炉的燃烧效率,即燃料燃烧加热水产生高温高压蒸汽。锅炉的燃烧效率的影响因素很多,包括锅炉的可调参数,如燃烧给量,一二次风,引风,返料风,给水水量;以及锅炉的工况,比如锅炉床温、床压,炉膛温度、压力,过热器的温度等。本次比赛,提供了经脱敏后的锅炉传感器采集的数据(采集频率是分钟级别),根据锅炉的工况,建立适当的模型来预测产生的蒸汽量。
第 2 章 模型简介
2.1 随机森林算法
随机森林算法是 近十几年兴起并发展的一种机器学习算法,有其独特的优势和特点。通过集成 多棵决策树来形成整个森林从而得出算法结果,因此随机森林算法本质上也属于集成学习算法。随机森林算法实现过程中,首先从所有样本中随机抽取相等数量的训练样本,然后从所有输人特征中选择 m 个子特征集,最后从子特征集中选取最优的一个属性进行节点分裂。随机森林算法 可以用于分类和回归问题。当解决分类问题时,每一棵决策树是分类树,分类时通过计算基尼 指数来进行结点分裂,最后的分类结果由所有决策树投票生成。当用于回归问题时,每一棵决 策树是回归树,通过最小均方差来划分,即对于划分特征对应的任意划分点两边将数据集划分成两个数据集, 使得划分后的两个数据集各自的均差最小,然后在分叉的两个节点处,继续利用这个原
则进行划分。最后的预测结果为所有决策树的均值。
第 3 章 数据分析
3.1 数据预处理
所有的变量如下表所示:
表 3-1 变量的设置、定义
| 变量名 | 变量说明 | |
| 因变量 | Target | 燃料燃烧加热水产生高温高压蒸汽 |
| 自变量 | V0,V1sV2,V3,V4,V5,V6,V7,V8,V9,V1 0,V11,V12,V13,V14,V15,V16,V17,V18,V19,V20,V21,V22,V23,V24,V25,V26,V27,V28,V29,V30,V31,V32,V33,V34,V35,V36,V37 | 锅炉燃烧效率的 38 个影响因素 |
将所搜集到各变量的原始数据进行标准化即无量纲化处理,以消除变量间在数量级上或量纲上的不同而产生的影响,结果使每个变量的平均值为 0,方差为 1。
3.1 模型选择
首先,本次比赛的目的在于对变量进行回归分析,根据因变量的数据类型,我们可以考虑多元最小二乘回归模型,但考虑到变量数量的庞大,极易出现多重共线性和异方差等问题。其次,本次比赛中变量真实含义未被公布,所以难以进行聚类分析从而理清数据内在结构特征。
故最终选择随机森林模型。该算法具有思路简单、容易实现的优点。在进行回归分析中,集成模型构建树时,样本由训练集又放回抽样得到。同时,在节点分割时,选择的分割点不是所有属性的最佳分割点,而是属性的随机子集中的最佳分割点。由于这种随机性,相对于单个非随机树,随机森林的偏差通常会有所增大,但由于取了平均,方差会减小,通常能够补偿偏差的增加,从而产生一个总体上更好的模型。
第 4 章 结果分析
4.1 决策树数目对预测准确度的影响
将训练样本导入 R 中,通过随机森林算法进行回归预测,其中 38 个特征为 38 个数值型自变量,target 为预测目标。当子特征数为默认值(即变量数目开根号)时,选取不同决策树数目进行回归预测,记录每次预测的均方误差(MSE),结果如下:
表 4-1 不同数量决策树时的结果
| 决策树数量 | |||||
| 100 | 150 | 200 | 250 | 300 | |
| 第一次 MSE | 0.122 | 0.121 | 0.120 | 0.121 | 0.120 |
| 第二次 MSE | 0.122 | 0.121 | 0.119 | 0.120 | 0.119 |
| 第三次 MSE | 0.123 | 0.122 | 0.121 | 0.120 | 0.120 |
| 平均 MSE | 0.122 | 0.121 | 0.120 | 0.120 | 0.120 |
| 总平均 MSE | 0.121 |
结合表 4-1 和图 4-1 可以看出,利用随机森林对因变量进行预测时,均方误差较小,
结果较为理想,当决策树数目达到 200 时,均方误差基本稳定。
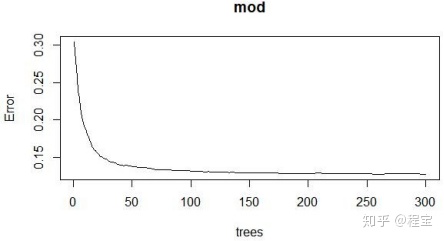
图 4-1 决策树数目对均方误差的影响
4.2 子特征数m 对决策准确度的影响
选取决策树 200 棵,子特征数 m=4,5,6,7,8,研究子特征数对预测误差的影响。结果见表 4-2 和图 4-2。可以看到,当子特征数逐渐增大时,MSE 逐渐减小,说明预测准确率逐渐增大。虽然随机森林算法预测每次都有一定的偶然性,看可以看出整体的效果还是不错的。可以看出,当子特征数为 8 时,均方误差最小。
表 4-2 不同子特征数的预测误差
| 子特征数的数量 | |||||
| 4 | 5 | 6 | 7 | 8 | |
| 第一次MSE | 0.126 | 0.123 | 0.122 | 0.123 | 0.120 |
| 第二次MSE | 0.126 | 0.123 | 0.124 | 0.122 | 0.121 |
| 第三次MSE | 0.128 | 0.124 | 0.124 | 0.122 | 0.121 |
| 平均 MSE | 0.137 | 0.123 | 0.123 | 0.122 | 0.121 |
| 总平均MSE | 0.123 |
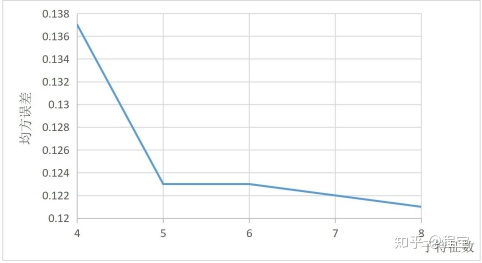
图 4-2 子特征数对 MSE 的影响
4.3 变量重要性
本文选择三个参量来计算变量重要性。
IncMSE,指均方根误差的增大程度,误差的增加等同于准确率的减少,该值越大
表示这个变量越重要。Mean Decrease of accuracy(MDA),是基于 OOB 误差,把其中一个变量的取值变为随机数随机森林预测准确度的降低程度,该值越大表示变量越重要。ImportanceSD,不同变量的标准差。
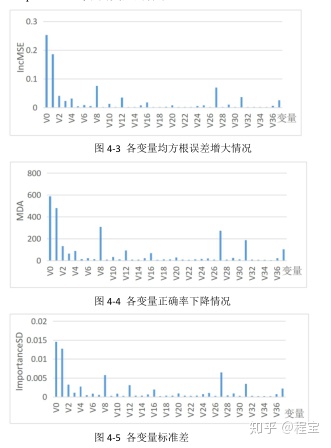
根据计算结果可以看出,变量 V0,V1,V8,V27 的重要程度相对较高,而变量
V2,V3,V4,V12,V31,V37 的变量重要性次之,其余变量重要性都较弱。
R语言代码展示:
### my code of case```{r cars}
setwd("G:/it'smypresentjob/competition")
library(randomForest)
library(varSelRF)
library(pROC)
data<- read.table("traindata.csv", header=TRUE, row.names="pid", sep=",")
t1<- read.table("testdata.csv", header=TRUE, row.names="id", sep=",")sV0<- scale(data2$V0)
sV1<- scale(data2$V1)
sV2<- scale(data2$V2)
sV3<- scale(data2$V3)
sV4<- scale(data2$V4)
sV5<- scale(data2$V5)
sV6<- scale(data2$V6)
sV7<- scale(data2$V7)
sV8<- scale(data2$V8)
sV9<- scale(data2$V9)
sV10<- scale(data2$V10)
sV11<- scale(data2$V11)
sV12<- scale(data2$V12)
sV13<- scale(data2$V13)
sV14<- scale(data2$V14)
sV15<- scale(data2$V15)
sV16<- scale(data2$V16)
sV17<- scale(data2$V17)
sV18<- scale(data2$V18)
sV19<- scale(data2$V19)
sV20<- scale(data2$V20)
sV21<- scale(data2$V21)
sV22<- scale(data2$V22)
sV23<- scale(data2$V23)
sV24<- scale(data2$V24)
sV25<- scale(data2$V25)
sV26<- scale(data2$V26)
sV27<- scale(data2$V27)
sV28<- scale(data2$V28)
sV29<- scale(data2$V29)
sV30<- scale(data2$V30)
sV31<- scale(data2$V31)
sV32<- scale(data2$V32)
sV33<- scale(data2$V33)
sV34<- scale(data2$V34)
sV35<- scale(data2$V35)
sV36<- scale(data2$V36)
sV37<- scale(data2$V37)
sVtarget<- scale(data2$target)data3<- cbind(sV0,sV1,sV2,sV3,sV4,sV5,sV6,sV7,sV8,sV9,sV10,sV11,sV12,sV13,sV14,sV15,sV16,sV17,sV18,sV19,sV20,sV21,sV22,sV23,sV24,sV25,sV26,sV27,sV28,sV29,sV30,sV31,sV32,sV33,sV34,sV35,sV36,sV37,sVtarget)
mod<-randomForest(x=data[,1:38],y=data[,39],ntree=100,importance=TRUE,keep.forest=TRUE)
modmod<-randomForest(x=data[,1:38],y=data[,39],ntree=100,importance=TRUE,keep.forest=TRUE)
modmod<-randomForest(x=data[,1:38],y=data[,39],ntree=100,importance=TRUE,keep.forest=TRUE)
modmod<-randomForest(x=data[,1:38],y=data[,39],ntree=150,importance=TRUE,keep.forest=TRUE)
modmod<-randomForest(x=data[,1:38],y=data[,39],ntree=150,importance=TRUE,keep.forest=TRUE)
modmod<-randomForest(x=data[,1:38],y=data[,39],ntree=150,importance=TRUE,keep.forest=TRUE)
modmod<-randomForest(x=data[,1:38],y=data[,39],ntree=200,importance=TRUE,keep.forest=TRUE)
modmod<-randomForest(x=data[,1:38],y=data[,39],ntree=200,importance=TRUE,keep.forest=TRUE)
modmod<-randomForest(x=data[,1:38],y=data[,39],ntree=200,importance=TRUE,keep.forest=TRUE)
modmod<-randomForest(x=data[,1:38],y=data[,39],ntree=250,importance=TRUE,keep.forest=TRUE)
modmod<-randomForest(x=data[,1:38],y=data[,39],ntree=250,importance=TRUE,keep.forest=TRUE)
modmod<-randomForest(x=data[,1:38],y=data[,39],ntree=250,importance=TRUE,keep.forest=TRUE)
modmod<-randomForest(x=data[,1:38],y=data[,39],ntree=300,importance=TRUE,keep.forest=TRUE)
modmod<-randomForest(x=data[,1:38],y=data[,39],ntree=300,importance=TRUE,keep.forest=TRUE)
modmod<-randomForest(x=data[,1:38],y=data[,39],ntree=300,importance=TRUE,keep.forest=TRUE)
modmod<-randomForest(x=traindata[,1:38],y=traindata[,39],mtry=4,ntree=200,importance=TRUE,keep.forest=TRUE)
modmod<-randomForest(x=traindata[,1:38],y=traindata[,39],mtry=4,ntree=200,importance=TRUE,keep.forest=TRUE)
modmod<-randomForest(x=traindata[,1:38],y=traindata[,39],mtry=4,ntree=200,importance=TRUE,keep.forest=TRUE)
modmod<-randomForest(x=traindata[,1:38],y=traindata[,39],mtry=5,ntree=200,importance=TRUE,keep.forest=TRUE)
modmod<-randomForest(x=traindata[,1:38],y=traindata[,39],mtry=5,ntree=200,importance=TRUE,keep.forest=TRUE)mod<-randomForest(x=traindata[,1:38],y=traindata[,39],mtry=5,ntree=200,importance=TRUE,keep.forest=TRUE)mod<-randomForest(x=traindata[,1:38],y=traindata[,39],mtry=6,ntree=200,importance=TRUE,keep.forest=TRUE)mod<-randomForest(x=traindata[,1:38],y=traindata[,39],mtry=6,ntree=200,importance=TRUE,keep.forest=TRUE)mod<-randomForest(x=traindata[,1:38],y=traindata[,39],mtry=6,ntree=200,importance=TRUE,keep.forest=TRUE)mod<-randomForest(x=traindata[,1:38],y=traindata[,39],mtry=7,ntree=200,importance=TRUE,keep.forest=TRUE)mod<-randomForest(x=traindata[,1:38],y=traindata[,39],mtry=7,ntree=200,importance=TRUE,keep.forest=TRUE)mod<-randomForest(x=traindata[,1:38],y=traindata[,39],mtry=7,ntree=200,importance=TRUE,keep.forest=TRUE)mod<-randomForest(x=traindata[,1:38],y=traindata[,39],mtry=8,ntree=200,importance=TRUE,keep.forest=TRUE)mod<-randomForest(x=traindata[,1:38],y=traindata[,39],mtry=8,ntree=200,importance=TRUE,keep.forest=TRUE)mod<-randomForest(x=traindata[,1:38],y=traindata[,39],mtry=8,ntree=200,importance=TRUE,keep.forest=TRUE)mod<-randomForest(x=traindata[ ,1:38],y=traindata[ ,39],mtry=8,ntree=200,importance=TRUE,keep.forest=TRUE)plot(mod)p_pred<-predict(mod, newdata=t1)mod$importancewrite.csv(p_pred,"G:/it'smypresentjob/competition/result.csv")