提出了一个最大化师生网络互信息作为知识转移的信息论框架。

主要贡献：

• 我们提出了变分信息提取，这是一种基于变分信息最大化技术，通过最大化两个网络之间的互信息实现的原则性知识转移框架。
• 我们证明了VID概括了几种现有的知识转移方法。此外，在各种知识转移实验中，我们的框架实现在经验上优于最先进的知识转移方法，包括相同数据集或不同数据集上（异构）DNN之间的知识转移。
• 最后，我们证明了在CIFAR-10上卷积神经网络（CNN）和多层感知器（MLP）之间的异构知识转移是可能的。我们的方法产生的学生MLP显著优于文献中报道的最佳MLP[17,27]。

VID

输入随机变量 x 考虑从 目标(结果)数据分布p（x）和 K 对层 R{（T^（k），S^（k））}_k＝1^K，其中每对（T^（k），S^（k））分别从教师网络和学生网络中选择。
通过网络对输入 x 进行前馈，产生 K 对随机变量 R{（t^（k），s^（k））}_k＝1^K，表示所选层的激活，t^（k）=T^（k）（x）。
随机变量对（t，s）之间的互信息定义如下:



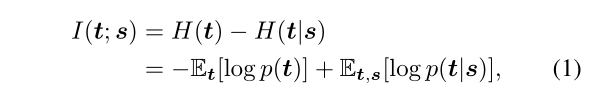
其中熵H（t）和 条件熵H（t | s）都来自联合分布p（t，s）。根据经验，联合分布p（t，s）是各层上的聚合结果，输入 x 从输入分布中采样p(x)。
直观地说，I（t；s）的定义可以理解为当学生层 s 已知时，教师在其层 t 中编码的知识的不确定性减少。现在，我们定义了以下损失函数，旨在学习目标任务的学生网络，同时鼓励与教师网络的高互信息：

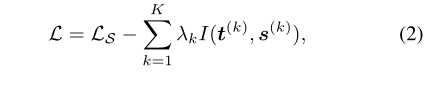
其中，L_S是目标任务的任务特定损失函数，λ_k>0是引入的超参数，用于正则化各层中的互信息。关于学生网络的参数，等式（2）需要最小化。然而，最小化是困难的，因为互信息的精确计算是困难的。相反，我们提出了每个互信息项I（t；s）的变分下界，其中我们定义了一个近似于p（t | s）的变分分布q（t | s）：

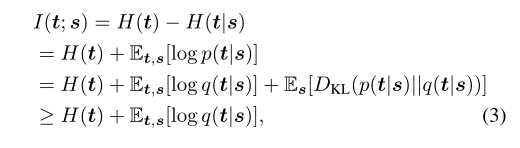
其中期望值超过分布p（t，s），最后一个不等式是由于Kullback-Leiber散度D_KL（·）的非负性。这种技术被称为变分信息最大化[1]。最后，我们通过对（2）中的每个互信息项 I（t^（k），s^（k））应用变分信息最大化来获得VID，从而使以下损失函数最小化：

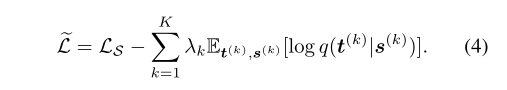
在学生网络参数和变分分布q（t | s）上，目标L被联合最小化。注意，熵项H（t）已从等式（3）中移除，因为它相对于待优化的参数是恒定的。或者，可以将目标（4）解释为联合训练学生网络以完成目标任务，并最大化条件可能性，以适应教师网络中选定层的激活。通过这样做，学生网络获得恢复教师网络中选定层的激活所需的“压缩”知识。

只能说太强了，勉强理解，经过推断，最后要求的就是

Algorithm formulation

我们通过选择变分分布q（t | s）的一种形式来进一步说明我们的框架。一般来说，我们采用具有异方差均值的高斯分布 µ(·) 和 同方差σ作为变分分布q（t | s），平均µ（·）是 s 的函数，标准偏差 σ 不 是。接下来，µ（·）和 σ 的参数化由对应于 t 的层的类型进一步指定。当 t 对应于教师网络的中间层时，其空间维度分别表示通道、高度和宽度，即t ∈ R^C×H×W，我们对变分分布的选择表示如下：


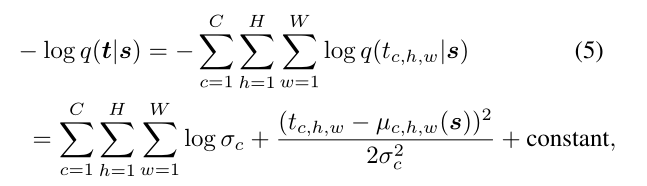
式中，t_c，h，w 的 c，h，w表示标量分量由（c，h，w）索引。此外，µ_c，h，w表示来自由卷积层组成的神经网络 µ（·）的单个单元的输出，并且使用softplus函数 i 确保方差为正。

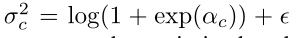
其中α_c∈ R是要优化的参数，并且 ε > 0 是数值稳定性引入的最小方差。通常，可以从与t具有类似层次结构和空间维度的学生网络中选择s。当两层的空间尺寸相等时，1×1卷积层通常用于µ（·）的有效参数化。否则，可以使用较大内核大小的卷积或转置卷积来匹配空间维度。

我们还考虑了当层 t= T^（logit）（x）∈ R^N 对应于教师网络的logit层。这里，我们对变分分布的选择表示如下：

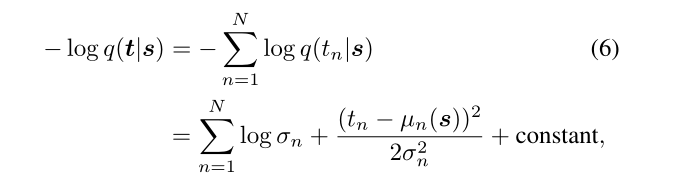
其中t_n表示向量t的第n个条目，µ_n 表示单个神经网络单位µ（·）和σ_n的输出，再次通过softplus函数进行参数化以增强正性。在这种情况下，学生网络中的对应层s是倒数第二层s^（pen），而不是logit层，以匹配两个层的层次结构，而不会对学生网络的输出造成太大限制。此外，我们发现使用简单的线性变换对平均函数进行参数化在实践中是足够的，即µ（s）= Ws 某些权重矩阵W的。

代码(重点在这,方便理解)

还可以参考这篇文章,我写的过余冗余了

from __future__ import print_functionimport torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as npclass VIDLoss(nn.Module):"""Variational Information Distillation for Knowledge Transfer (CVPR 2019),code from author: https://github.com/ssahn0215/variational-information-distillation"""def __init__(self,num_input_channels,num_mid_channel,num_target_channels,init_pred_var=5.0,eps=1e-5):super(VIDLoss, self).__init__()def conv1x1(in_channels, out_channels, stride=1):return nn.Conv2d(in_channels, out_channels,kernel_size=1, padding=0,bias=False, stride=stride)self.regressor = nn.Sequential(conv1x1(num_input_channels, num_mid_channel),nn.ReLU(),conv1x1(num_mid_channel, num_mid_channel),nn.ReLU(),conv1x1(num_mid_channel, num_target_channels),)self.log_scale = torch.nn.Parameter(np.log(np.exp(init_pred_var-eps)-1.0) * torch.ones(num_target_channels))self.eps = epsdef forward(self, input, target):# pool for dimentsion matchs_H, t_H = input.shape[2], target.shape[2]if s_H > t_H:input = F.adaptive_avg_pool2d(input, (t_H, t_H))elif s_H < t_H:target = F.adaptive_avg_pool2d(target, (s_H, s_H))else:passpred_mean = self.regressor(input)pred_var = torch.log(1.0+torch.exp(self.log_scale))+self.epspred_var = pred_var.view(1, -1, 1, 1)neg_log_prob = 0.5*((pred_mean-target)**2/pred_var+torch.log(pred_var))loss = torch.mean(neg_log_prob)return loss