cn.wordpress.org/seo搜索优化是什么

我发现网上很多人将的都不清楚，如果只看文章的话，根本就理解不了。所以在我研究完代码之后记录下来，方便次观看，如果有益于跟多人的话那更好了。
写下的都是自己的理解，如果有误欢迎订正。
这里以大根堆举例，适时的会说一下小根堆
讲解代码

说在前面

首先，了解一下大根堆or小根堆 （下面简称’堆’）的性质。

1. 堆是一个完全二叉树（最后一层可以不满，上面的每一层都是满的。一个结点若只有一个孩子结点，那一定是它的左孩子。如下图）
   

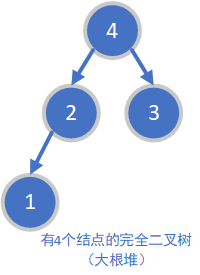
2. 因为它是一个完全二叉树，所以它也就可以用数组存储。具有以下特殊关系：
   下标为 i 的结点的父节点的下标是 （i - 1）/ 2；
   一个下标为 j的 结点，若它有孩子结点，则它的左孩子结点为 (2 * i) + 1; 右孩子结点为 （2 * i ）+ 2;
   

3. 大根堆的任何一非叶节点的值大于其左右孩子节点的值。小根堆的任何一非叶节点的值小于其左右孩子节点的值。所以这要求构建堆的类型可以比较大小，不然没有意义。但是没有要求左右两个孩子的值的大小。

两个重要函数siftDown() 和 siftUp()

先说堆中用到的两个函数siftDown()和siftUp()。

//在i的儿子中选最大的,如果最大的大于i和i交换位置private void siftDown(int i) {if(i >= size / 2 ) return;		//如果i大于等于最后一个结点的叔叔结点，那么说明i是叶子结点，无需Down、返回。int index;      //  最大的儿子下标if((2 * i) + 2 >= size) {index = (2 * i) + 1;} else{index = (data[(2 * i) + 2] > data[(2 * i) + 1]) ? (2 * i) + 2 : (2 * i) + 1;}if(data[index] > data[i]) {int temp = data[i];data[i] = data[index];data[index] = temp;siftDown(index);}}

siftDown函数是将非叶子结点和其孩子结点进行比较，大根堆是将值大的选出来，值小的Down；小根堆是将值小的选出来，值大的Down。
这里写的是递归调用，退出条件是：i是叶子结点时退出。这里的写的（i >= size / 2）很巧妙。 写成（i > (size - 2) / 2）i大于最后一个结点的父节点的话，如果只有两个元素时（i == 0 , (size - 2 ) / 2 == 0），就不会对0结点进行比较。

	private void siftUp(int index) {if(index == 0) return;if(data[index] > data[(index - 1) / 2]){int temp = data[(index - 1) / 2];data[(index - 1) / 2] = data[index];data[index] = temp;siftUp((index - 1) / 2);}}

siftUp是将index结点和它的父节点进行比较，大根堆是将值大Up，小根堆是将值小的Up。
这个很好理解。递归调用，当传入的是根节点时退出。

堆的建立

初始输入为一个数组。

	public Heap (int[] data){this.data = data;size = data.length;heapify();			//将输入的data数组构建成大根堆}

构造函数，将一个数组构造成堆，调用堆化函数heapify()，初始化堆。

//堆化private void heapify() {for(int i = (size - 2) / 2; i >= 0; i--){siftDown(i);}}

从最后一个结点的父节点开始遍历，使所有非叶子结点都进行siftDown操作。

插入结点

	public void insert(int number){if(size == data.length)resize();data[size++] = number;siftUp(size-1);}private void resize(){data = Arrays.copyOf(data,data.length * 2);}

插入很简单，将要插入的结点加到最后，然后对新插入的结点进行siftUp操作就行了。

删除结点

	public int delete(int index){if(index >= size) return -1;		//下标超界返回-1int temp = data[index];				//存储要删去的值int record = data[size - 1];		//记录最后一个结点的值data[index] = data[--size];			//将最后一个结点覆盖要删去结点的位置siftDown(index, size);if(record == data[index])siftUp(index);return temp;}

因为不知道最后一个结点的值的大小和要删除的结点值的关系，所以先siftDown操作，如果没有变化，再进行siftUp操作。

看图说话，第三步如果如果Down了，说明最后一个元素比删除元素小，就没有Up的必要了。如果第3步没变，想想如果有四层，要删除的在倒数第二层，也有可能最后一个元素比删除的上一个元素大，所以就进行Up操作。

堆排序

重点就是将上面最大的元素放在最后一个位置，然后忽略它。
修改一下siftDown操作。

	//在i的儿子中选最大的,如果最大的大于i和i交换位置private void siftDown(int i,int size) {if(i >= size / 2 ) return;		//如果i大于等于最后一个结点的叔叔结点，那么说明i是叶子结点，无需Down、返回。int index;      //  最大的儿子下标if((2 * i) + 2 >= size) {index = (2 * i) + 1;} else{index = (data[(2 * i) + 2] > data[(2 * i) + 1]) ? (2 * i) + 2 : (2 * i) + 1;}if(data[index] > data[i]) {int temp = data[i];data[i] = data[index];data[index] = temp;siftDown(index, size);}}

巧就巧在将size修改为局部变量，这样就可以修改局部传入参数的值来忽略最后一个元素了。

	//大根堆默认升序排序public void Sort(){int mysize = size;for(; mysize > 0;){int temp = data[0];data[0] = data[--mysize];data[mysize] = temp;siftDown(0, mysize);			//交换第一个和最后一个元素后对下标为0的第一个元素进行siftDown操作。}}

遍历size 个元素所以时间复杂度为 nlogn

全部代码

import java.util.Arrays;
/*
* 默认是大根堆
* */
public class Heap<E extends Number & Comparable<E>> {private final int DEFAULT_CAPACITY = 10;private E[] data;private int size;public Heap(){data = (E[]) new Number[DEFAULT_CAPACITY];size = 0;}public Heap (E[] data){this.data = data;size = data.length;heapify();}//堆化private void heapify() {for(int i = (size - 2) / 2; i >= 0; i--){siftDown(i, size);}}//在i的儿子中选最大的,如果最大的大于i和i交换位置private void siftDown(int i, int size) {if(i >= size / 2 ) return;int index;      //  最大的儿子下标if((i << 1) + 2 >= size) {index = (i << 1) + 1;} else{index = (data[(i << 1) + 2].compareTo(data[(i << 1) + 1]) > 0) ? (i << 1) + 2 : (i << 1) + 1;}if(data[i].compareTo(data[index]) < 0) {E temp = data[i];data[i] = data[index];data[index] = temp;siftDown(index, size);}}public void insert(E number){if(size == data.length)resize();data[size++] = number;riseUp(size-1);}public E delete(E number){for(int i = 0; i < size; i++){if(data[i].equals(number))return delete(i);}return null;}public E delete(int index){if(index >= size) return null;E temp = data[index];E record = data[size - 1];data[index] = data[--size];siftDown(index, size);if(record == data[index])riseUp(index);return temp;}private void riseUp(int index) {if(index == 0) return;if(data[index].compareTo(data[(index - 1) / 2]) > 0){E temp = data[(index - 1) / 2];data[(index - 1) / 2] = data[index];data[index] = temp;riseUp((index - 1) / 2);}}//大根堆默认升序排序public void Sort(){int mysize = size;for(; mysize > 0;){E temp = data[0];data[0] = data[--mysize];data[mysize] = temp;siftDown(0, mysize);}}//还原排序后的大根堆public void reBack(){heapify();}private void resize(){data = Arrays.copyOf(data,data.length * 2);}@Overridepublic String toString() {String res = "";res += "Heap{data = [";for (int i = 0; i < size - 1; i++){res += data[i].toString() + ", ";}if(size != 0){res += data[size - 1];}res +="]}";return res;}
}