网站建设与推广好做吗/网站关键词优化案例
点上面的小灰框就可以关注我的视频号啦！
建议大家先戳下面的小程序看视频(因为是B站链接可能清晰度不够高)。后面是图文版本~
01前两天我在微博上问大家想听我做什么选题，结果一堆人都在问如何脱单！主要都是女生在问！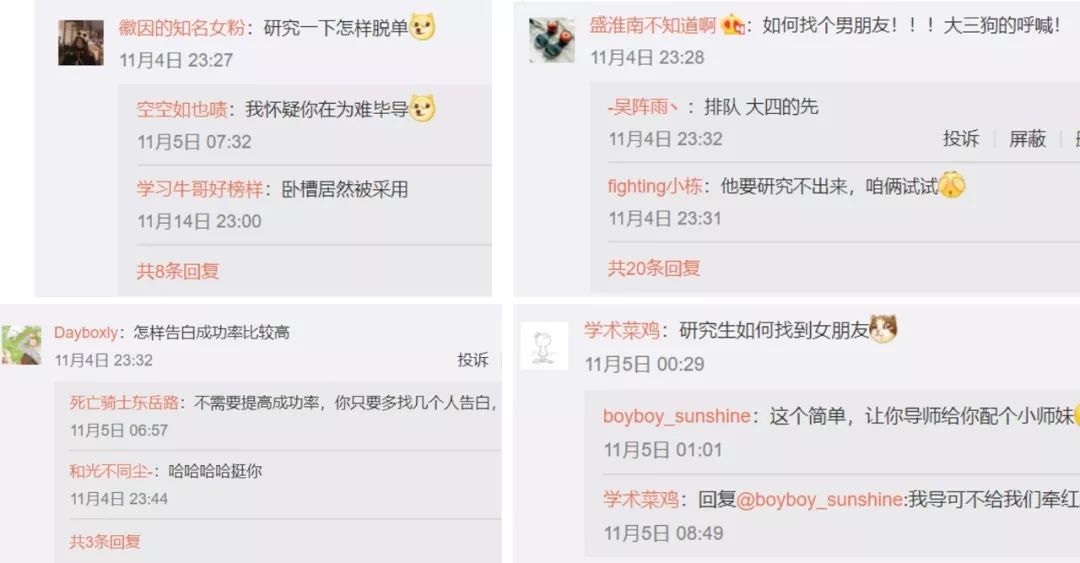
尽管脱单问题不属于科学，对于有钱人属于经济学，对穷人属于玄学，但我还是勉为其难地给大家分析一下“如何科学脱单”。先说一个我自己的小故事。我刚上大学的时候要参加新生舞会，毕竟清华工科班，本来就没几个女生，你不赶紧抢，女生就没了。
虽然那时候我长这样，好在我脸皮厚，全班第一个约到了舞伴。
结果舞会当天，我们发现一件神奇的事情，我们班的班花竟然落单了！她自己都尴尬！早知道当时我就去邀请她了！现在估计孩子都上小学二年级了！后来我们才得知，当年的真相是这样的：
02你一生中会遇到很多男生，有没有什么科学的策略，能找到那个最优秀的男生呢？(注意，下面我们都以学术研究的视角来分析，不考虑找对象中存在的道德问题。)我们类比地思考，假设你到公共厕所，想找到一个最满意的马桶，没有前人的残留，有合适的温度，有崭新的卷纸。你会怎么做呢？通常你会依次拉开门看一眼，感觉某一个马桶差不多满意，就坐下。
其实男生就是马桶。女生面对追求者时总希望能找到最好的马桶。你通常会一个个试过去，遇到一个差不多满意的就停，然后在一起，尽管未来还可能有更好的。这类问题在数学上被称为“最优停止问题”[1]，它有一个很巧妙的策略。假设一个女生遇到了三个男生。如果她两眼一闭，随机选择，那有1/3的概率选到最优秀的男生。但其实她还有一种先舍后得的策略：先跟第一个男生处一处，不管他好不好都果断分手；然后考察第二个男生，如果他比第一个男生优秀，就正式在一起；如果他不如第一个男生，那就分手，和第三个男生在一起。这种策略看似耍流氓，但对于三个男生一共有6种排序，采用这种策略，我们以1为最好，3为最差，排查一下：
看到了没！这种策略比盲选厉害多了！所以鲁迅先生早就说过：初恋不值得！它只是寻找真爱的垫脚石。情场老手一般都会先随意谈上几段恋情，观察一下整体情况，然后再做出决策。那么最好的策略是观察多少个人呢[2]？假设一共有n个人备选，你先观察观察前k个人，但都放弃，从第k+1个人开始，一旦遇到一个比前面都优秀的，就和他在一起。
我们来求一下k等于多少的时候， 我们有把握和最优秀的人在一起。我们在小学二年级的时候就学过条件概率和黎曼和。设选到最优秀男生的概率P(k)，则有
此时问题转化为超简单的整数规划问题
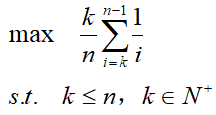在n较小时，直接一波非线性规划或者动态规划就能求解了[3]，无非是在n!种情况中找出最优的情况。比如n=4的时候甚至可以直接穷举出最优解为k=1，概率P(1)=11/24。
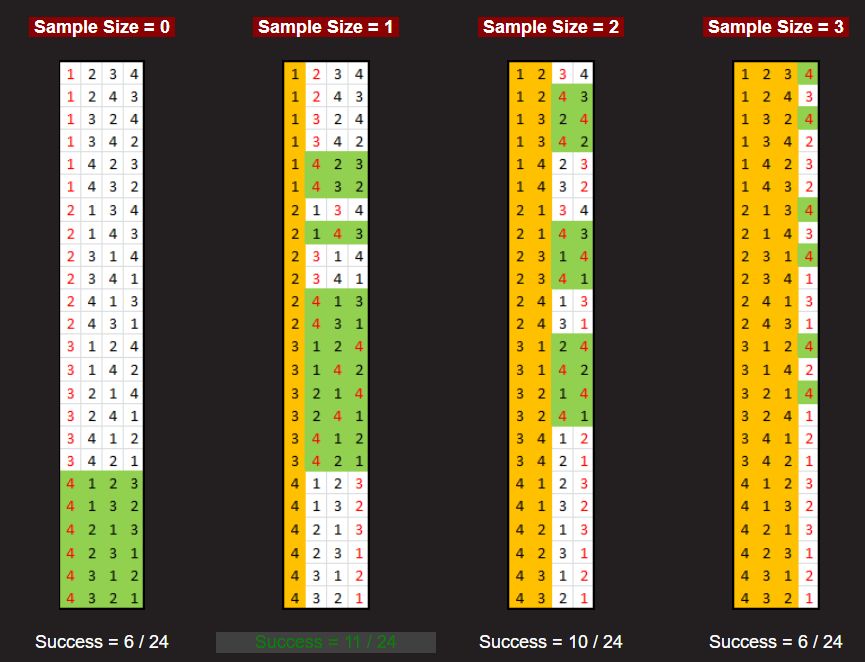在n很大时，注意到目标函数
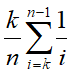的形式即是y=1/x，将区间(k/n,1)分割成若干个宽度为1/n的小区间后求积分的黎曼和。直接令x=k/n，则原式变成了积分问题
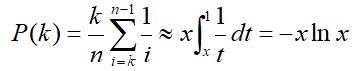为求P(k)的最大值，令
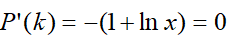求得
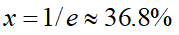且有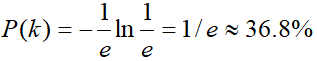
惊讶地发现这还是个不动点啊！结论太美妙了！也就是说，如果你面前有n个男生备选，最佳策略就是，先观察37%的男生，但都不要在一起，从37%往后，一旦遇到一个比前面男生都好的，就果断出手！此时命中最优男生的概率也是37%！这就是著名的“37%法则”。假设你每年遇到的男生数量一样，如果找对象决策期是15岁到35岁，那22.4岁之前就是观察期，之后遇到更好的，就结婚！我们来编个程模拟一下，首先生成一个女生，给她随机分配100个不同的男生。用蒙特卡罗模拟100万次。结果非常amazing！她有37%的概率选中最优秀的男生，14%的概率选中第二优秀的，7%概率选中第三优秀的。
更具体地，这个概率分布函数是这样的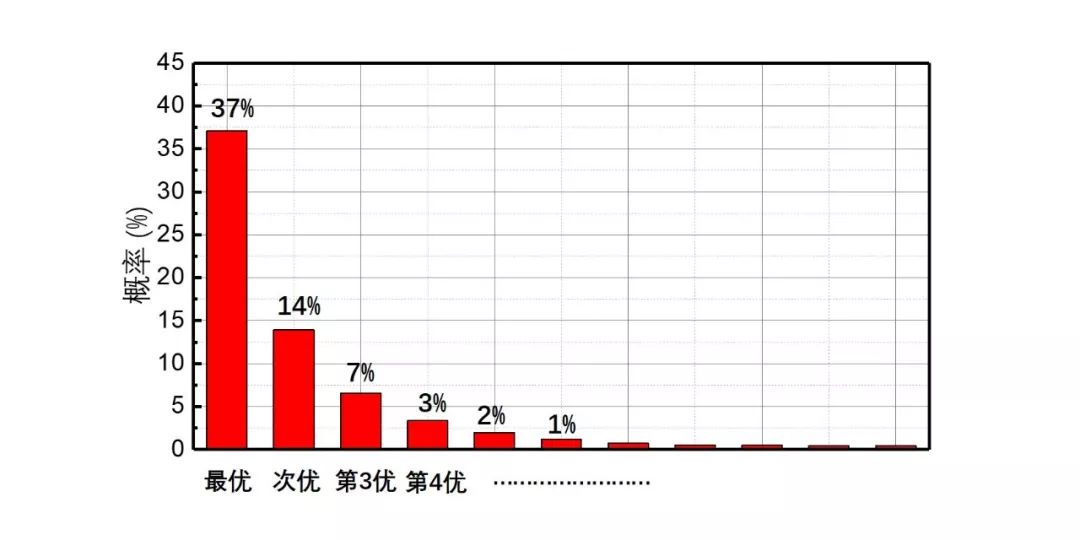
有的观众可能会说，我压根就不会遇到100个能看上我的异性啊！没关系，我又计算了面对0-20个男生情况下的概率[4]。如果随机盲选，你选到最优男生的概率就是1/n，不如自挂东南枝，凑合过上一辈子。但只要你运用37%法则，你选到最佳男生的概率永远高于37%，在天愿作比翼鸟，在地一起吃烧烤。
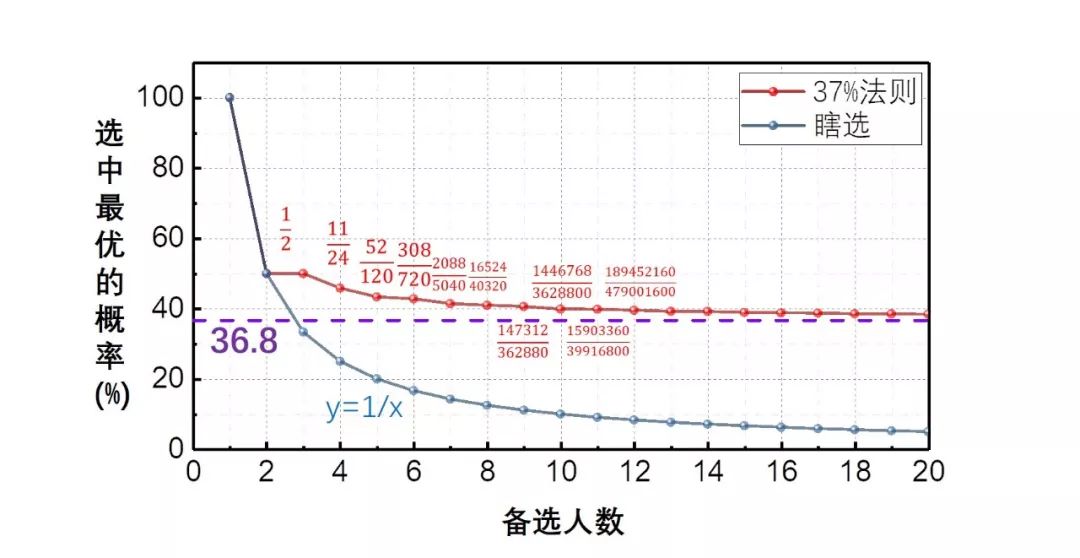不过在n≤2时两条线是重合的。也就是说，如果世界上只有一两个人喜欢你的话，也就没必要折腾什么策略了，瞎选吧。有的观众可能又会说，你这个计算不科学啊！你这也太理想了，实际生活中对方根本不可能让我随便挑啊！我出手了人家可能拒绝我啊！没关系，我又对模型进行了修正，考虑到每次面对男生只有p的概率被对方接受，有(1-p)的概率被男生拒绝，则策略就得进行调整[5]。这是一个非常有趣的问题，我在此试着详细讲解一下这个问题。我们用X和Y两个随机变量来描述候选男生。定义随机变量Xr为男生r相对于他之前的人的排名，定义0-1随机变量Yr为申请人r是否依概率p接受了女生，易得X与Y的概率分布
那么本问题就是要在(X1,Y1)，(X2,Y2)，...，(XN,YN)这样一些组合中确定一个最优的停止规则，从而以最大的概率选中最优的人。用Ur(k,i)表示当我们考查完Xr=k，Yr=i的后停止的效用，那其实k=1且i=1时表示排第1的被我们拿下了，因此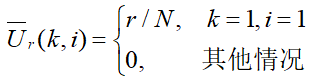
即是Xr=k且Yr=i时申请人r为最佳的概率。此时有向后递推公式，E代表期望
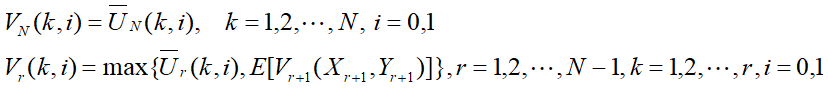设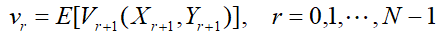
那么最优策略如下：Xr=1,Yr=1，且vr≤r/N。而v0也即是选中最优男生的最大概率。
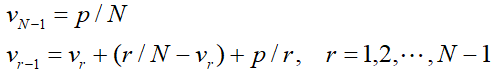因此vr随r减少，而r/N随r增加，存在一个r*使得vr≤r/N，当且仅当r≥r*。解得
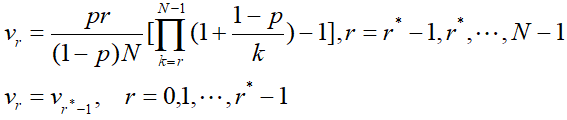此时的最大概率v0
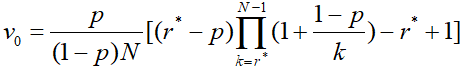下面求r*，不等式放缩有
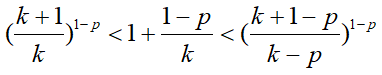r*的定义保证了
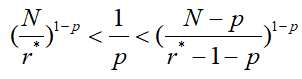故有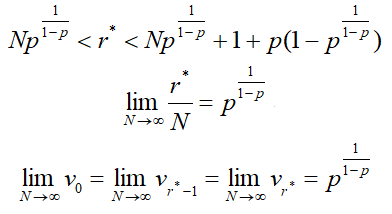
最后这个结论很美妙。它说明在有接受概率p的情况下，最优的策略是一个仅和p相关的函数，且依然是一个不动点！当p=0时，代表对方100%拒绝你，这时候也就别谈恋爱了。当p=1时，问题退化为原37%法则问题，此时结果的极限亦是37%。
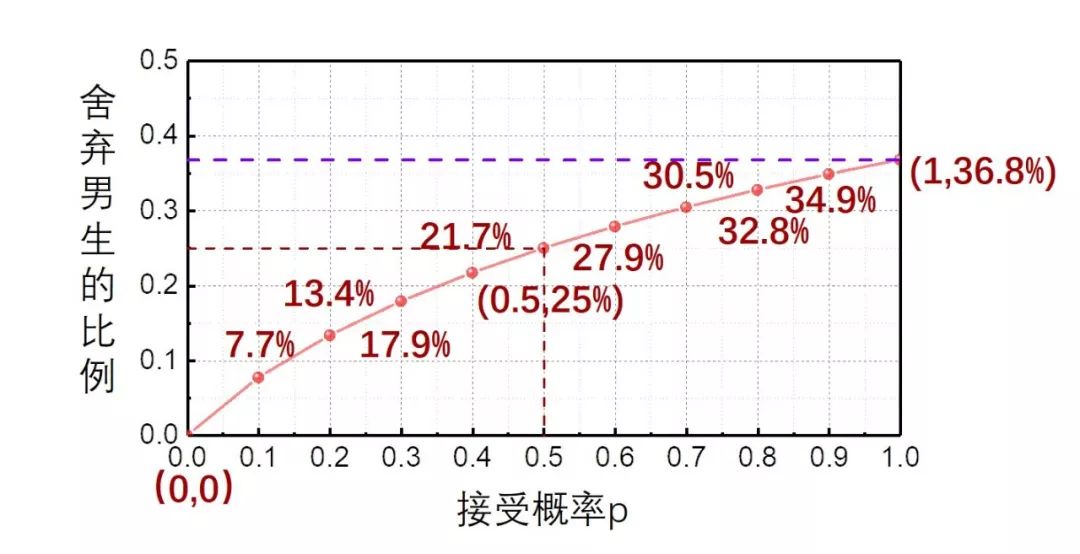由图可见，如果你有一半概率被人拒绝，就应该把37%法则修正成25%法则，也就是观察前25%的人之后就出手。如果你越辣鸡，被拒绝的概率越大，你就应该缩短观察期，越早出手。所以我妈从小就教育我，人丑就要早出手，不然就成单身狗。有人又问了，现实生活中我特么怎么知道我的n是多少？有文献专门研究过如果n值是未知的，我应该采取啥策略[6]。但文献我真没看懂，你们自己看吧……关于如何增大自己的n，我只能告诉大家一些生活经验了！
参考文献1、最优停止问题维基百科，https://en.wikipedia.org/wiki/Secretary_problem#CITEREFFerguson19892、最优停止问题综述，Freeman P R. The secretary problem and its extensions: A review[J]. International Statistical Review, 1983, 51(2): 189-206.3、线性规划法硬解最优停止问题，Buchbinder N, Jain K, Singh M. Secretary problems via linear programming[C]//International Conference on Integer Programming and Combinatorial Optimization. Springer, Berlin, Heidelberg, 2010: 163-176.4、一个算37%法则非常厉害的网站，http://datagenetics.com/blog/december32012/index.html5、带拒绝概率p的变体问题，Smith M H. A secretary problem with uncertain employment[J]. Journal of applied probability, 1975, 12(3): 620-624.6、n未知时的算法，Horiguchi M, Yasuda M. The best choice problem for random number of objects with a refusal probability[J]. Preprint. Available at http://www. math. s. chibau. ac. jp/yasuda/accept/cornel/INFORMSdoc. pdf, 2009.
评论区的(3、4楼)，(11、12楼)，(17、18楼)、(29、30楼)我将会让你们交换联系方式！如果想找对象的话，正好认识认识！不想找对象的话，大家都是毕导粉丝也差不到哪去！(当然前提是征得你们同意)
建议大家先戳下面的小程序看视频(因为是B站链接可能清晰度不够高)。后面是图文版本~01前两天我在微博上问大家想听我做什么选题，结果一堆人都在问如何脱单！主要都是女生在问！
尽管脱单问题不属于科学，对于有钱人属于经济学，对穷人属于玄学，但我还是勉为其难地给大家分析一下“如何科学脱单”。先说一个我自己的小故事。我刚上大学的时候要参加新生舞会，毕竟清华工科班，本来就没几个女生，你不赶紧抢，女生就没了。虽然那时候我长这样，好在我脸皮厚，全班第一个约到了舞伴。结果舞会当天，我们发现一件神奇的事情，我们班的班花竟然落单了！她自己都尴尬！早知道当时我就去邀请她了！现在估计孩子都上小学二年级了！后来我们才得知，当年的真相是这样的：班草在想，要是他邀请班花被拒绝了，那岂不是很没面子，肯定会被全班人嘲笑四年，如果邀请其他人就稳妥多了。
像我这样的普通群众在想，班草肯定会去邀请班花，人家郎才女貌，我干嘛自取其辱？
02你一生中会遇到很多男生，有没有什么科学的策略，能找到那个最优秀的男生呢？(注意，下面我们都以学术研究的视角来分析，不考虑找对象中存在的道德问题。)我们类比地思考，假设你到公共厕所，想找到一个最满意的马桶，没有前人的残留，有合适的温度，有崭新的卷纸。你会怎么做呢？通常你会依次拉开门看一眼，感觉某一个马桶差不多满意，就坐下。其实男生就是马桶。女生面对追求者时总希望能找到最好的马桶。你通常会一个个试过去，遇到一个差不多满意的就停，然后在一起，尽管未来还可能有更好的。这类问题在数学上被称为“最优停止问题”[1]，它有一个很巧妙的策略。假设一个女生遇到了三个男生。如果她两眼一闭，随机选择，那有1/3的概率选到最优秀的男生。但其实她还有一种先舍后得的策略：先跟第一个男生处一处，不管他好不好都果断分手；然后考察第二个男生，如果他比第一个男生优秀，就正式在一起；如果他不如第一个男生，那就分手，和第三个男生在一起。这种策略看似耍流氓，但对于三个男生一共有6种排序，采用这种策略，我们以1为最好，3为最差，排查一下：123，则舍弃1-舍弃2-选中3
132，则舍弃1-舍弃3-选中2
213，则舍弃2-选中1
231，则舍弃2-舍弃3-选中1
312，则舍弃3-选中1
321，则舍弃3-选中2
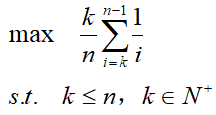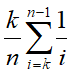看到了没！这种策略比盲选厉害多了！所以鲁迅先生早就说过：初恋不值得！它只是寻找真爱的垫脚石。情场老手一般都会先随意谈上几段恋情，观察一下整体情况，然后再做出决策。那么最好的策略是观察多少个人呢[2]？假设一共有n个人备选，你先观察观察前k个人，但都放弃，从第k+1个人开始，一旦遇到一个比前面都优秀的，就和他在一起。我们来求一下k等于多少的时候， 我们有把握和最优秀的人在一起。我们在小学二年级的时候就学过条件概率和黎曼和。设选到最优秀男生的概率P(k)，则有此时问题转化为超简单的整数规划问题在n较小时，直接一波非线性规划或者动态规划就能求解了[3]，无非是在n!种情况中找出最优的情况。比如n=4的时候甚至可以直接穷举出最优解为k=1，概率P(1)=11/24。在n很大时，注意到目标函数的形式即是y=1/x，将区间(k/n,1)分割成若干个宽度为1/n的小区间后求积分的黎曼和。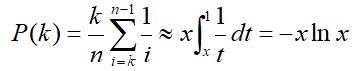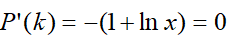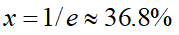直接令x=k/n，则原式变成了积分问题为求P(k)的最大值，令求得且有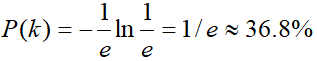惊讶地发现这还是个不动点啊！结论太美妙了！也就是说，如果你面前有n个男生备选，最佳策略就是，先观察37%的男生，但都不要在一起，从37%往后，一旦遇到一个比前面男生都好的，就果断出手！此时命中最优男生的概率也是37%！这就是著名的“37%法则”。假设你每年遇到的男生数量一样，如果找对象决策期是15岁到35岁，那22.4岁之前就是观察期，之后遇到更好的，就结婚！我们来编个程模拟一下，首先生成一个女生，给她随机分配100个不同的男生。用蒙特卡罗模拟100万次。结果非常amazing！她有37%的概率选中最优秀的男生，14%的概率选中第二优秀的，7%概率选中第三优秀的。更具体地，这个概率分布函数是这样的有的观众可能会说，我压根就不会遇到100个能看上我的异性啊！没关系，我又计算了面对0-20个男生情况下的概率[4]。如果随机盲选，你选到最优男生的概率就是1/n，不如自挂东南枝，凑合过上一辈子。但只要你运用37%法则，你选到最佳男生的概率永远高于37%，在天愿作比翼鸟，在地一起吃烧烤。不过在n≤2时两条线是重合的。也就是说，如果世界上只有一两个人喜欢你的话，也就没必要折腾什么策略了，瞎选吧。有的观众可能又会说，你这个计算不科学啊！你这也太理想了，实际生活中对方根本不可能让我随便挑啊！我出手了人家可能拒绝我啊！没关系，我又对模型进行了修正，考虑到每次面对男生只有p的概率被对方接受，有(1-p)的概率被男生拒绝，则策略就得进行调整[5]。这是一个非常有趣的问题，我在此试着详细讲解一下这个问题。我们用X和Y两个随机变量来描述候选男生。定义随机变量Xr为男生r相对于他之前的人的排名，定义0-1随机变量Yr为申请人r是否依概率p接受了女生，易得X与Y的概率分布那么本问题就是要在(X1,Y1)，(X2,Y2)，...，(XN,YN)这样一些组合中确定一个最优的停止规则，从而以最大的概率选中最优的人。用Ur(k,i)表示当我们考查完Xr=k，Yr=i的后停止的效用，那其实k=1且i=1时表示排第1的被我们拿下了，因此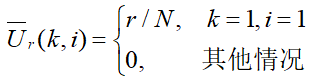即是Xr=k且Yr=i时申请人r为最佳的概率。此时有向后递推公式，E代表期望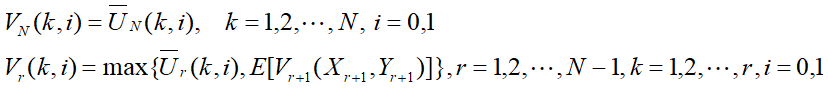设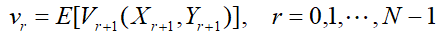那么最优策略如下：Xr=1,Yr=1，且vr≤r/N。而v0也即是选中最优男生的最大概率。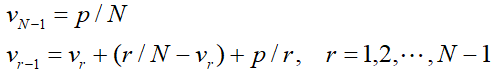因此vr随r减少，而r/N随r增加，存在一个r*使得vr≤r/N，当且仅当r≥r*。解得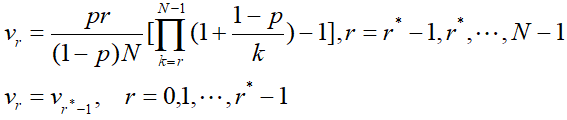此时的最大概率v0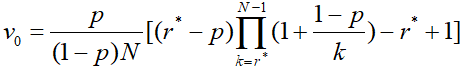下面求r*，不等式放缩有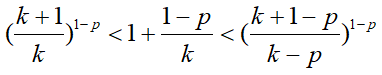r*的定义保证了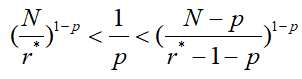故有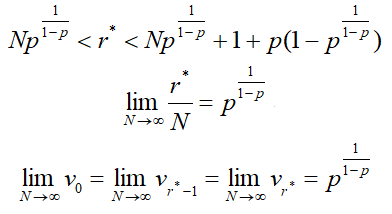最后这个结论很美妙。它说明在有接受概率p的情况下，最优的策略是一个仅和p相关的函数，且依然是一个不动点！当p=0时，代表对方100%拒绝你，这时候也就别谈恋爱了。当p=1时，问题退化为原37%法则问题，此时结果的极限亦是37%。由图可见，如果你有一半概率被人拒绝，就应该把37%法则修正成25%法则，也就是观察前25%的人之后就出手。如果你越辣鸡，被拒绝的概率越大，你就应该缩短观察期，越早出手。所以我妈从小就教育我，人丑就要早出手，不然就成单身狗。有人又问了，现实生活中我特么怎么知道我的n是多少？有文献专门研究过如果n值是未知的，我应该采取啥策略[6]。但文献我真没看懂，你们自己看吧……关于如何增大自己的n，我只能告诉大家一些生活经验了！多发点体现你热爱生活的朋友圈。现代人社交都很谨慎的！多给别人点话题，不然谁来找你说话啊，话都没得说还能咋约会。
报个班学点东西，或者报个社团、旅游之类的。增大n值最好的方法就是强行增大n值。
少宅，多和朋友聊聊天，你妈让你相亲别拒绝，也许对方挺好看呢。
主动当个好人。这条有点虚无，但我建议女生朋友们不要居高临下地考察男生，不要总是把想法憋在心里然后暗中观察男生会不会对自己好。大家都很忙的，你有意思你就主动一点。
参考文献1、最优停止问题维基百科，https://en.wikipedia.org/wiki/Secretary_problem#CITEREFFerguson19892、最优停止问题综述，Freeman P R. The secretary problem and its extensions: A review[J]. International Statistical Review, 1983, 51(2): 189-206.3、线性规划法硬解最优停止问题，Buchbinder N, Jain K, Singh M. Secretary problems via linear programming[C]//International Conference on Integer Programming and Combinatorial Optimization. Springer, Berlin, Heidelberg, 2010: 163-176.4、一个算37%法则非常厉害的网站，http://datagenetics.com/blog/december32012/index.html5、带拒绝概率p的变体问题，Smith M H. A secretary problem with uncertain employment[J]. Journal of applied probability, 1975, 12(3): 620-624.6、n未知时的算法，Horiguchi M, Yasuda M. The best choice problem for random number of objects with a refusal probability[J]. Preprint. Available at http://www. math. s. chibau. ac. jp/yasuda/accept/cornel/INFORMSdoc. pdf, 2009.
评论区的(3、4楼)，(11、12楼)，(17、18楼)、(29、30楼)我将会让你们交换联系方式！如果想找对象的话，正好认识认识！不想找对象的话，大家都是毕导粉丝也差不到哪去！(当然前提是征得你们同意)