小语种网站建设/武汉今日头条最新消息
本文内容来自学习麻省理工学院公开课:单变量微积分-隐函数微分法和逆函数导数-网易公开课
开发环境准备:CSDN
目录
一、 公式推导
二、 例子求导
三、公式推导
一、  公式推导
公式推导
由链式法则:
由
由此公式 (n的取值范围扩大到所有整数和分数)
二、 例子求导 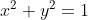
验证下:
from sympy import *
x= symbols('x')
y = (1-x**2)**0.5
dif = diff(y, x)
dif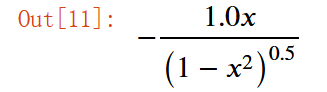
这里老师提到隐函数微分:
(可以看到和上面的结果一致)
看看导数对不对得上:
import numpy as np
import matplotlib.pyplot as plt radius = 1
angle = np.linspace( 0 , 2 * np.pi , 150 )
x = radius * np.cos( angle )
y = radius * np.sin( angle ) figure, axes = plt.subplots( 1 ) axes.plot( x, y, label='x^2+y^2=1, radius:'+format(radius) )
axes.set_aspect( 1 ) x, y, x0, y0 = symbols('x y x0 y0')
expr = (y-y0)/(x-x0) + x0/(1-x0**2)**(0.5)
expr = expr.subs(y0,(1-x0**2)**0.5)
expr = expr.subs(x0,0.6)
yarr = []xarr = np.linspace(-1 , 2.5 , 25 )
for xval in xarr:yexpr = expr.subs(x,xval)eqy = Eq(yexpr, 0)soly = solve(eqy)yarr.append(soly)y_nparr = np.array(yarr) plt.plot(xarr, y_nparr, color='b', label='tangent line of fx on x=0.6')plt.legend(loc='upper right')
plt.show() 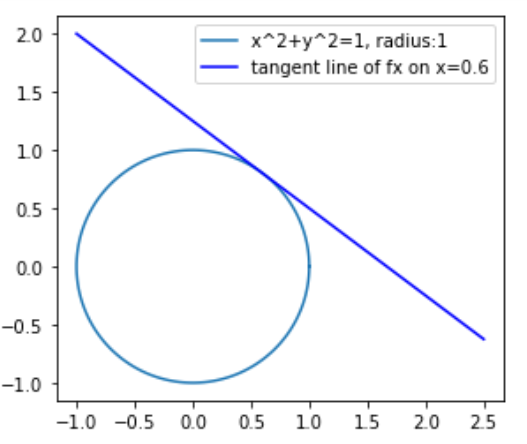
三、公式推导
显式求导
(须知:一元二次方程: , 求根公式:
)
.....
隐式求导:
