一个好的网站应该具有什么/如何建网站赚钱

  对于(看作几何空间)而言，一张不过原点的平面是不能成为一个线性空间的，因为这个平面上两个向量的差：

并不位于上，但如果另有一个与其平行的平面过原点：

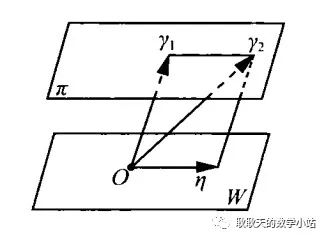
则便是一个线性子空间，且位于中。

  一个想法是：考察所有这样与给定的平行的平面组成的集合，则这个集合恰好是整个空间的一个划分。而如果规定二元关系：

则这个关系是一个等价关系(读者自行验证)，且其等价类恰好是与平行的平面组成的集合。这种观点能让我们从另一角度看待线性空间的结构，因此也有研究的价值。

  定义1 设是数域上的线性空间， 为的一个子空间，称由等价关系

所诱导的所有等价类的集合为的商空间，记为。对于一个给定的，称集合

为的陪集，记作，称为这个陪集的代表。

  商空间是否是一个线性空间？直观上我们想为规定元素的加法和数量乘法为：

但这可能会出现一个问题：对于和，如果

则这种加法连一个二元运算都不是了：它没有为同一个陪集规定一个唯一的像。以几何空间为例说明，取为的直线，那么应当保证图中两组向量的加法

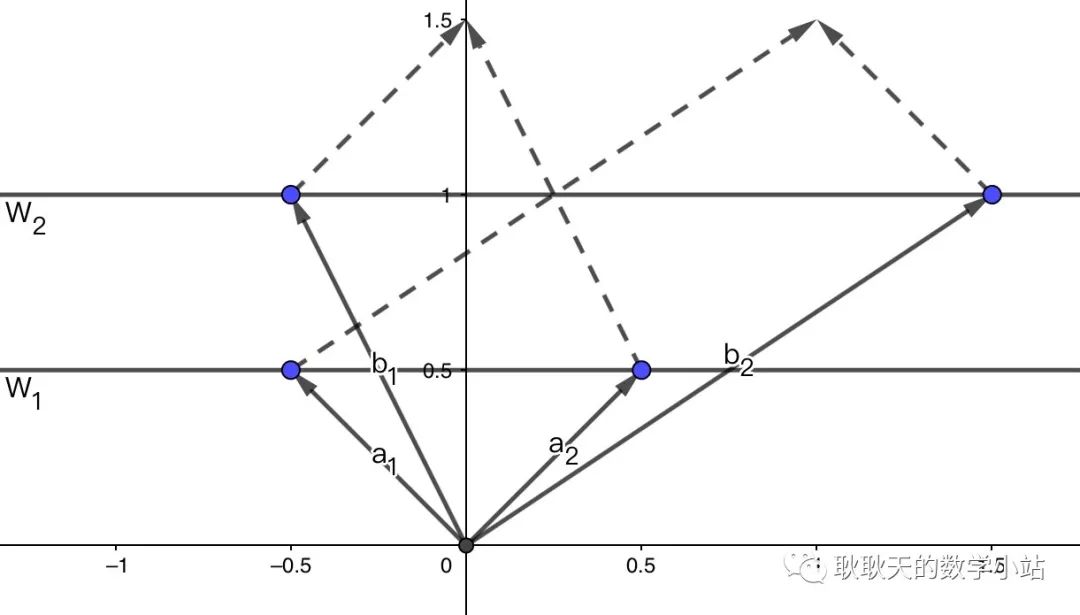
总在同一条水平线上，这样才能得到一个唯一确定的新陪集。

  可以证明这一点是能够保证的，请读者自行考虑。类似也可说明数量乘法保证这一点，并且它们都满足线性空间所需条件，于是成为了上的线性空间，其中为其零向量，为的负向量。

  定理1 

  证明 取的一组基并扩充为的一组基，下证：任取，设

则

若存在不全为零的使得

则也有

矛盾。

  到其商空间有一个非常自然的映射：

我们称之为自然映射或标准映射或典范映射。由定义可知这显然是个满射，而由定理1可知为非零子空间时这不是一个单射，因为对任意都有，即商空间中一个元素的原像是 的一个配集。

  另外可以验证这个映射还是线性的，从而商空间中线性无关的向量组的原像向量组也是线性无关的。这一性质使得我们能够利用商空间的结构加以研究原空间的结构，我们用下面的定理来说明这一点。

  定理2 上的线性空间的任一子空间都有补空间。

  证明 设的一组基为，则也是中的线性无关组，记这组向量生成的子空间为，下证便是在中的补空间：首先所代表的配集都可由线性表出：

这就说明存在使得

即。另外任取，并由设

另一方面又由知

而是线性无关的，可见从而，即。