贪心

贪心：每一步行动总是按某种指标选取最优的操作来进行， 该指标只看眼前，并不考虑以后可能造成的影响。

局部最优 → 整体最优。

区间问题

区间选点

给定 N 个闭区间 [ai,bi][ai,bi]，请你在数轴上选择尽量少的点，使得每个区间内至少包含一个选出的点。

输出选择的点的最小数量。

位于区间端点上的点也算作区间内。

输入格式

第一行包含整数 N，表示区间数。

接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两个端点。

输出格式

输出一个整数，表示所需的点的最小数量。

数据范围

1≤N≤105,
−109≤ai≤bi≤109

此题同理：最大不相交区间数量

给定 NN 个闭区间 [ai,bi][ai,bi]，请你在数轴上选择若干区间，使得选中的区间之间互不相交（包括端点）。

思路：

右端点排序，直接对比。下面是题解

左端点排序的话，逆序对比。

#include<iostream>
#include<algorithm>
using namespace std;const int N = 1e5+10;
pair<int,int> v[N];
bool cmp(pair<int,int> a,pair<int,int> b)
{return a.second<b.second;
}
int main(void)
{int n;scanf("%d",&n);for(int i=0;i<n;i++)cin>>v[i].first>>v[i].second;sort(v,v+n,cmp);int res = 0,ed = -2e9;for(int i=0;i<n;i++){if(v[i].first>ed) {res++;ed = v[i].second;}}cout<<res;
}

区间合并

给定 N 个闭区间 [ai,bi][ai,bi]，请你将这些区间分成若干组，使得每组内部的区间两两之间（包括端点）没有交集，并使得组数尽可能小。

输出最小组数。

输入格式

第一行包含整数 N，表示区间数。

接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两个端点。

输出格式

输出一个整数，表示最小组数。

数据范围

1≤N≤105,
−109≤ai≤bi≤109

左端点排序：

1.逻辑解释：

当第cnt个区间的左端点小于前cnt - 1个区间的最小的max_r时，前cnt -1个区间的左端点不一定都小于第cnt个区间的左端点，因为是按照右端点排序的。如果有些区间的左端点大于第cnt个区间的左端点，并且大于另一些区间的max_r，就不能保证这cnt个区间都有一个共同点（就是第cnt个区间的左端点）。

2.反证解释：

按照右边排序的话，各个区间的左端点不能保证单调性，所以有可能第三个区间的左端点比第一个区间的左端点还要左边，它可以特别长。

反例： [1, 3], [2, 5], [4, 100], [10, 13]

3.比喻：

比如，有n个人需要用教室，每个人占用教室的起始时间和终止时间是不一样的。
1、如果想知道只有一间教室，能安排下的最多不冲突人数（不是所有的人都有机会，有的会被舍掉）是多少（区间选点和最大不相交问题），那么当然是最先结束的人排在前面，这样后面的人才有更多机会。如果是按左端点排序，那么如过一个人0点开始用，那么肯定他排在最前面，但是如果他自己就占用了24小时，那么只能给他一个人用了，这样就达不到最大的效果。所以按左端点排序。
2、如果想知道这些人都必须安排，没有人被舍弃，至少需要多少个教室能安排下（区间分组问题）。那么肯定是按照开始时间排序，开始时间越早越优先。这样每间教室都能得到最充分的利用。

---

偷偷说：实际按左右无所谓的。这题的区间只是一个一维坐标系，如果要按右端点排序，那你就从右往左找 min_r 好了。只是一个方向问题。

思路：

1.将所有区间按左端点从小到大排序

2.从前往后判断 ： if L[i] > Max_r ，即是否能将其放到某个现有的组中

​ ①如果存在，将其放进去，并更新当前组的 MAX_r

​ ②如果不存在，开新组，然后再将其放进去

#include <iostream>
#include <algorithm>
#include <queue>using namespace std;const int N = 100010;int n;
struct Range
{int l, r;bool operator< (const Range &W)const{return l < W.l;}
}range[N];int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ ){int l, r;scanf("%d%d", &l, &r);range[i] = {l, r};}sort(range, range + n);priority_queue<int, vector<int>, greater<int>> heap;for (int i = 0; i < n; i ++ ){//小根堆里存的是每个分组的最大右端点，//当前要判断的区间的左端点至少要大于其中一个分组的最大右端点，才会用更新替代开新组。auto it = range[i];if (heap.empty() || heap.top() >= it.l) heap.push(it.r); //开新组else{heap.pop();         //不开组，更新当前组的MAX_r。heap.push(it.r);}}printf("%d\n", heap.size());return 0;
}

区间覆盖

给定 N 个闭区间 [ai,bi][ai,bi] 以及一个线段区间 [s,t][s,t]，请你选择尽量少的区间，将指定线段区间完全覆盖。

输出最少区间数，如果无法完全覆盖则输出 −1。

输入格式

第一行包含两个整数 s 和 t，表示给定线段区间的两个端点。

第二行包含整数 N，表示给定区间数。

接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两个端点。

输出格式

输出一个整数，表示所需最少区间数。

如果无解，则输出 −1。

数据范围

1≤N≤105,
−109≤ai≤bi≤109,
−109≤s≤t≤109

思路：

1.从左到右按左端点排序

2.从前往后依次枚举每个区间，在所有能覆盖start的区间中，选择右端点最大的区间，

然后将start更新成右端点最大值

#include <iostream>
#include <algorithm>using namespace std;const int N = 100010;int n;
struct Range
{int l, r;bool operator< (const Range &W)const{return l < W.l;}
}range[N];int main()
{int st, ed;scanf("%d%d", &st, &ed);scanf("%d", &n);for (int i = 0; i < n; i ++ ){int l, r;scanf("%d%d", &l, &r);range[i] = {l, r};}sort(range, range + n);int res = 0;bool success = false;for (int i = 0; i < n; i ++ ){int j = i, r = -2e9;while (j < n && range[j].l <= st){r = max(r, range[j].r);j ++ ;}if (r < st){res = -1;break;}res ++ ;if (r >= ed){success = true;break;}st = r;i = j - 1;}if (!success) res = -1;printf("%d\n", res);return 0;
}

Q :最后为什么是i=j-1 而不是i=j ?

A :比如说： j扫描到了 2 此时while() 退出了 我们下次 i 应该从 2开始但是需要注意的是我们的for()循环 i++ ,i还会加1次 此时 我们的 i=3 直接从 3 开始循环了，故需要减1。

Q ：那为什么不把i++去掉，然后i = j好理解一点

A ：因为j不一定会++,这样可能会死循环

哈夫曼树（堆）

合并果子

在一个果园里，达达已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。

达达决定把所有的果子合成一堆。

每一次合并，达达可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。

可以看出，所有的果子经过 n−1n−1 次合并之后，就只剩下一堆了。

达达在合并果子时总共消耗的体力等于每次合并所耗体力之和。

因为还要花大力气把这些果子搬回家，所以达达在合并果子时要尽可能地节省体力。

假定每个果子重量都为 11，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使达达耗费的体力最少，并输出这个最小的体力耗费值。

例如有 33 种果子，数目依次为 1，2，91，2，9。

可以先将 1、21、2 堆合并，新堆数目为 33，耗费体力为 33。

接着，将新堆与原先的第三堆合并，又得到新的堆，数目为 1212，耗费体力为 1212。

所以达达总共耗费体力=3+12=15=3+12=15。

可以证明 15 为最小的体力耗费值。

输入格式

输入包括两行，第一行是一个整数 n，表示果子的种类数。

第二行包含 n 个整数，用空格分隔，第 i 个整数 ai 是第 i种果子的数目。

输出格式

输出包括一行，这一行只包含一个整数，也就是最小的体力耗费值。

输入数据保证这个值小于 231。

数据范围

1≤n≤10000,
1≤ai≤20000

#include<iostream>
#include<queue>
using namespace std ;
int res;
int main(void)
{priority_queue<int,vector<int>,greater<int> > heap;int n;cin>>n;while(n--) {int x ;scanf("%d",&x);heap.push(x);}while(heap.size()>1){int a = heap.top();heap.pop();int b = heap.top();heap.pop();res += a+b;heap.push(a+b);}printf("%d",res);}

排序不等式

排队打水

有 n 个人排队到 11 个水龙头处打水，第 ii 个人装满水桶所需的时间是 ti，请问如何安排他们的打水顺序才能使所有人的等待时间之和最小？

输入格式

第一行包含整数 n。

第二行包含 n 个整数，其中第 i 个整数表示第 i 个人装满水桶所花费的时间 ti。

输出格式

输出一个整数，表示最小的等待时间之和。

数据范围

1≤n≤105,
1≤ti≤104

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e5+10;
long long res;
int main(void)
{int a[N],n;cin>>n;for(int i = 0;i<n;i++){cin>>a[i];}sort(a,a+n);for(int i=0;i<n;i++){res += a[i]*(n-1-i);}cout<<res;
}

绝对值不等式

货仓选址

在一条数轴上有 N 家商店，它们的坐标分别为 A1∼AN。

现在需要在数轴上建立一家货仓，每天清晨，从货仓到每家商店都要运送一车商品。

为了提高效率，求把货仓建在何处，可以使得货仓到每家商店的距离之和最小。

输入格式

第一行输入整数 N。

第二行 N 个整数 A1∼AN。

输出格式

输出一个整数，表示距离之和的最小值。

数据范围

1≤N≤1000001≤N≤100000,
0≤Ai≤40000

#include<iostream>
#include<algorithm>
using namespace std ;
const int N = 1e5+10;
int n;
int a[N];
int res;
int main(void)
{scanf("%d",&n);for(int i=0;i<n;i++){scanf("%d",&a[i]);}sort(a,a+n);for(int i=0;i<n;i++){res += abs(a[i]-a[n/2]);}cout<<res;
}

推出来的不等式

耍杂技的牛

农民约翰的 N 头奶牛（编号为1…N）计划逃跑并加入马戏团，为此它们决定练习表演杂技。

奶牛们不是非常有创意，只提出了一个杂技表演：

叠罗汉，表演时，奶牛们站在彼此的身上，形成一个高高的垂直堆叠。

奶牛们正在试图找到自己在这个堆叠中应该所处的位置顺序。

这 N 头奶牛中的每一头都有着自己的重量 Wi 以及自己的强壮程度 Si。

一头牛支撑不住的可能性取决于它头上所有牛的总重量（不包括它自己）减去它的身体强壮程度的值，现在称该数值为风险值，风险值越大，这只牛撑不住的可能性越高。

您的任务是确定奶牛的排序，使得所有奶牛的风险值中的最大值尽可能的小。

输入格式

第一行输入整数 N，表示奶牛数量。

接下来 N 行，每行输入两个整数，表示牛的重量和强壮程度，第 i 行表示第 i 头牛的重量 Wi 以及它的强壮程度 Si。

输出格式

输出一个整数，表示最大风险值的最小可能值。

数据范围

1≤N≤50000,
1≤Wi≤10,000,
1≤Si≤1,000,000,000

既然是推出来的不等式，下面来贴下推理过程：

/	交换前	交换后
第i头牛	W1+W2+…W(i-1) - Si	W1+…Wi-1+Wi+1 - Si
第i+1头牛	W1+W2+…Wi - S(i+1)	W1+…Wi-1 - S(i+1)

去掉重复的W1+…W(i-1) , 得

/	交换前	交换后
第i头牛	- Si	Wi+1 - Si
第i+1头牛	Wi - S(i+1)	- S(i+1)

题目所求答案为危险系数最大值的最小值，所以找到最大值就OK。

对于上表，易知 Wi -S(i+1) > -S(i+1) , Wi+1-Si > -Si ；

故交换前取最大值 Wi -S(i+1) ,交换后去最大值 Wi+1-Si 。

假设交换后，我们得到的是最小值（这样假设得到的式子能够帮助我们求得答案），则有不等式：

Wi - S(i+1) > Wi+1 - Si ，即交换后变小。

移项得 Wi + Si > Wi+1 + Si+1 。

此时我们发现，设 Q = W+S ，只需要按照Q对输入排序(也就是完成交换的过程)，再依次比较。

取Q1 … Qi 中的最小值即可。

#include <iostream>
#include <algorithm>using namespace std;typedef pair<int, int> PII;const int N = 50010;int n;
PII cow[N];int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ ){int s, w;scanf("%d%d", &w, &s);cow[i] = {w + s, w};}sort(cow, cow + n);int res = -2e9, sum = 0;for (int i = 0; i < n; i ++ ){int s = cow[i].first - cow[i].second, w = cow[i].second;res = max(res, sum - s);sum += w;}printf("%d\n", res);return 0;
}

以前的题

圣诞节来临了，圣诞老人准备分发糖果，现

在有多箱不同的糖果，每箱糖果有自己的价值和重

量，每箱糖果都可以拆分成任意散装组合带走。圣

诞老人的驯鹿雪橇最多只能装下重量W的糖果，请

问圣诞老人最多能带走多大价值的糖果。

#include<iostream>
#include<algorithm>
#include<memory.h>
#include<iomanip>
const  double eps = 1e-6;
using namespace std;
int W;
double V;
struct suger{int w;int v;bool operator<(const suger& s){return double(v)/w-double(s.v)/s.w>eps;}
}sugers[110];
void greedy(int &total,int &n){for(int i=0;i<n;i++){if(total+sugers[i].w<=W){total += sugers[i].w;V += sugers[i].v;}else {V += sugers[i].v* double(W-total)/sugers[i].w;			W = W+W-total;break;}}
}
int main(void)
{int n,total=0;cin>>n>>W;for(int i=0;i<n;i++){cin>>sugers[i].v>>sugers[i].w;}sort(sugers,sugers+n);//自己写greedy(total,n);cout<<fixed<<setprecision(1)<<V;}

各地放了多部电影 ，给定每部电影的放映时间区间，区间重叠的电影不可能同时

看（端点可以重合），问李雷最多可以看多少部电影。

int total;
struct film{int s;int e;bool operator<(const film& f){return e<f.e;} 
}f,films[110];
int main(void)
{   int n;cin>>n;for(int i=0;i<n;i++){cin>>films[i].s>>films[i].e;}sort(films,films+n);total++;f=films[0];for(int i=1;i<n;i++){if(f.e<=films[i].s){total++;f=films[i];}}cout << endl<<total;
}

有 n头牛（1<=n<=50,000)要挤奶。给定每头牛挤奶的时间区

间[A,B] (1<=A<=B<=1,000,000，A,B为整数)。

牛需要呆畜栏里才能挤奶。一个畜栏同一时间只能容纳一头牛。

问至少需要多少个畜栏，才能完成全部挤奶工作，以及每头牛都

放哪个畜栏里（Special judged)

去同一个畜栏的两头牛，它们挤奶时间区间哪怕只在端点重合也

是不可以的。

//难点：优先队列的运用 + 配合贪心和队列的排序
//（奶牛和栅栏的顺序定义operator，栅栏和奶牛都需要no来记录原顺序编号） 
#include<iostream>                     //（因为它们都被排序打乱了 ） 
#include<algorithm> //ps：循环均为从1开始
#include<queue>
using namespace std;
struct cow{int s;//时间区间 start -end int e;int no; //奶牛编号：防止原奶牛顺序 由于进入时间的排序而被打乱 operator<(const cow& c){ //排序 return s<c.s;}
}cows[100];
int pos[100];
typedef struct fence{int e;//栅栏的结束时间不断在变 ，作为队列排序依据int no; //栅栏编号，方便记录奶牛进入的栅栏（同样是防止队列顺序更新而失去原顺序编号） bool operator<(const fence & f) const {return e > f.e; }fence(int e,int n):e(e),no(n){};// 对栅栏赋值。 
}fen;
int total; //栅栏数 
int main(void)
{  //1.奶牛赋值+排序 int n;cin>>n;for(int i=1;i<=n;i++){cin>>cows[i].s>>cows[i].e;cows[i].no=i;//排序前，在赋值no过程记录好原位置 }sort(cows+1,cows+n+1); //2.栅栏赋值+排序 priority_queue<fen> pq;for(int i=1;i<=n;i++){	if(pq.empty()){//情况1.最开始（无奶牛） ++total;pq.push(fen(cows[i].e,total));pos[cows[i].no]=total;}else { //情况2. next奶牛与目前栅栏冲突 fen f=pq.top();//利用排序（目前结束最快） 找到待命栅栏 if(f.e>=cows[i].s){++total;pq.push(fen(cows[i].e,total)); //冲突加入新栅栏，编号即total pos[cows[i].no]=total;}else {//情况3. 不冲突 //不冲突：total不变，队列弹出原奶牛，压入新奶牛 pq.pop();                 pos[cows[i].no]=f.no;    //进入编号为top（待命）的栅栏 pq.push(fen(cows[i].e,f.no)); //不冲突使用原栅栏}}}//3.循环结束，事件结束,输出 cout<< total<<endl;for(int i=1;i<=n;i++)cout<<pos[i]<<endl;
}

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YwPjrjKm-1684146461476)(data:image/gif;base64,R0lGODlhAQABAPABAP///wAAACH5BAEKAAAALAAAAAABAAEAAAICRAEAOw==)]

放置雷达：

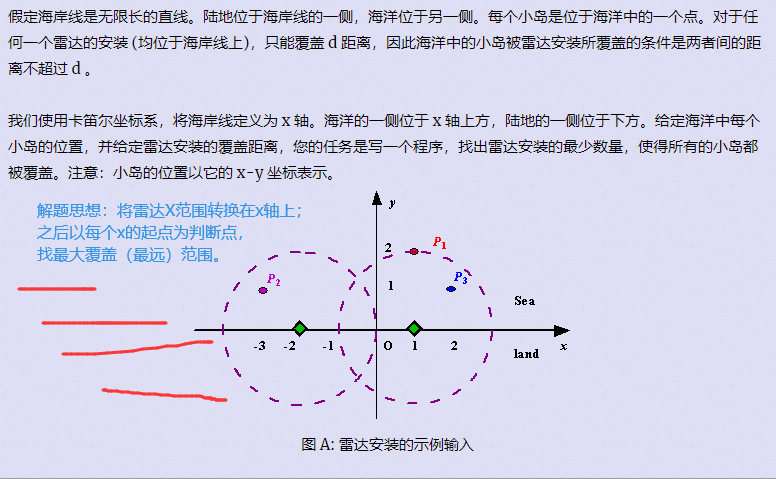[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-k2PNb52e-1684146461477)(data:image/gif;base64,R0lGODlhAQABAPABAP///wAAACH5BAEKAAAALAAAAAABAAEAAAICRAEAOw==)]

#include<iostream>
#include<vector>
#include<cmath>
#include<algorithm>
using namespace std;
int n,d,total;
class how{public:bool operator()(pair<double,double> p1,pair<double,double> p2){return p1.first<p2.first;}
};
bool decide(vector<pair<double,double> > m,int F,int i)
{for(int k=F;k<i;k++){if(m[i].first<=m[k].second&&m[i].first>=m[k].first)continue;else return false;}return true;}
void dfs(const vector<pair<double,double> >&m)
{int FNC=0;while(1){   int i;for(i=FNC+1;i<n;i++){  if(decide(m,FNC,i)) continue;else{FNC=i;total++;break;}} if(i>=n) {total++;break;}}}
int flag=1;
int main(void)
{   while(cin>>n>>d&&n!=0){total=0;vector<pair<double,double> > m;for(int i=0;i<n;i++){int x,y;cin>>x>>y;pair<double,double> p;p.first =x-sqrt(d*d-y*y);p.second=x+sqrt(d*d-y*y);m.push_back(p);}sort(m.begin(),m.end(),how());dfs(m);cout<<"case"<<flag<<":"<<total<<endl;flag++;}
}