自己网站做seo/百度客服人工电话

大家好呀！在上一篇文章《风控建模中的自动分箱的方法有哪些》中我们介绍了3种业界常用的自动最优分箱方法。
1）基于CART算法的连续变量最优分箱
2）基于卡方检验的连续变量最优分箱
3）基于最优KS的连续变量最优分箱
今天这篇文章就来分享一下这3种方法的Python实现。

00 Index

01 测试数据与评估方法准备
02 基于CART算法的最优分箱代码实现
03 基于卡方检验的最优分箱代码实现
04 基于最优KS的最优分箱代码实现
05 测试效果与小节

01 测试数据与评估方法准备

为了模拟实际在风险建模中我们常遇见的数据集，我这边简单造了一些数据，主要有3列：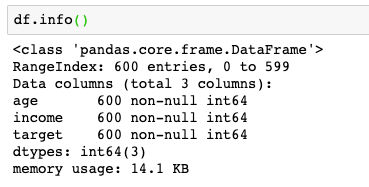
其中，target就是我们的Y列，另外两个分别是X列，也就是我们的特征。
我们需要做的就是把数据导入即可，数据集可以在公众号（SamShare）后台回复 cut 获取。

# 导入相关库
import pandas as pd
import numpy as np
import random
import math
from scipy.stats import chi2
import scipy# 测试数据构造，其中target为Y，1代表坏人，0代表好人。  
df = pd.read_csv('./autocut_testdata.csv')
print(len(df))
print(df.target.value_counts()/len(df))
print(df.head())

另外，我们需要一个评估分箱效果的方法，上篇我们讲到可以用IV值来衡量效果，所以我们需要也构造一个IV值计算的方法。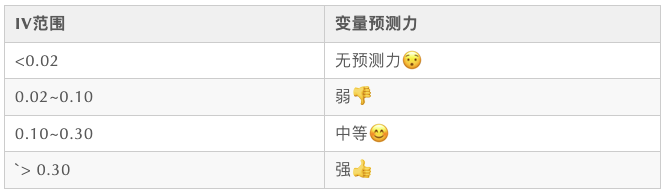

def iv_count(data, var, target):''' 计算iv值Args:data: DataFrame，拟操作的数据集var: String，拟计算IV值的变量名称target: String，Y列名称Returns:IV值， float'''value_list = set(list(np.unique(data[var])))iv = 0data_bad = pd.Series(data[data[target]==1][var].values, index=data[data[target]==1].index)data_good = pd.Series(data[data[target]==0][var].values, index=data[data[target]==0].index)len_bad = len(data_bad)len_good = len(data_good)for value in value_list:# 判断是否某类是否为0，避免出现无穷小值和无穷大值if sum(data_bad == value) == 0:bad_rate = 1 / len_badelse:bad_rate = sum(data_bad == value) / len_badif sum(data_good == value) == 0:good_rate = 1 / len_goodelse:good_rate = sum(data_good == value) / len_goodiv += (good_rate - bad_rate) * math.log(good_rate / bad_rate,2)# print(value,iv)return iv

02 基于CART算法的最优分箱代码实现

基于CART算法的连续变量最优分箱，实现步骤如下：
1，给定连续变量 V，对V中的值进行排序；
2，依次计算相邻元素间中位数作为二值划分点的基尼指数；
3，选择最优（划分后基尼指数下降最大）的划分点作为本次迭代的划分点；
4，递归迭代步骤2-3，直到满足停止条件。（一般是以划分后的样本量作为停止条件，比如叶子节点的样本量>=总样本量的10%）

def get_var_median(data, var):""" 得到指定连续变量的所有元素的中位数列表Args:data: DataFrame，拟操作的数据集var: String，拟分箱的连续型变量名称Returns:关于连续变量的所有元素的中位列表，List"""var_value_list = list(np.unique(data[var]))var_median_list = []for i in range(len(var_value_list)-1):var_median = (var_value_list[i] + var_value_list[i+1]) / 2var_median_list.append(var_median)return var_median_listdef calculate_gini(y):""" 计算基尼指数Args:y: Array，待计算数据的target，即0和1的数组Returns:基尼指数，float"""# 将数组转化为列表y = y.tolist()probs = [y.count(i)/len(y) for i in np.unique(y)]gini = sum([p*(1-p) for p in probs])return ginidef get_cart_split_point(data, var, target, min_sample):""" 获得最优的二值划分点（即基尼指数下降最大的点）Args:data: DataFrame，拟操作的数据集var: String，拟分箱的连续型变量名称target: String，Y列名称min_sample: int，分箱的最小数据样本，也就是数据量至少达到多少才需要去分箱，一般作用在开头或者结尾处的分箱点Returns:BestSplit_Point: 返回本次迭代的最优划分点，floatBestSplit_Position: 返回最优划分点的位置，最左边为0，最右边为1，float"""# 初始化Gini = calculate_gini(data[target].values)Best_Gini = 0.0BestSplit_Point = -99999BestSplit_Position = 0.0median_list = get_var_median(data, var) # 获取当前数据集指定元素的所有中位数列表for i in range(len(median_list)):left = data[data[var] < median_list[i]]right = data[data[var] > median_list[i]]# 如果切分后的数据量少于指定阈值，跳出本次分箱计算if len(left) < min_sample or len(right) < min_sample:continueLeft_Gini = calculate_gini(left[target].values)Right_Gini = calculate_gini(right[target].values)Left_Ratio = len(left) / len(data)Right_Ratio = len(right) / len(data)Temp_Gini = Gini - (Left_Gini * Left_Ratio + Right_Gini * Right_Ratio)if Temp_Gini > Best_Gini:Best_Gini = Temp_GiniBestSplit_Point = median_list[i]# 获取切分点的位置，最左边为0，最右边为1if len(median_list) > 1:BestSplit_Position = i / (len(median_list) - 1)else:BestSplit_Position = i / len(len(median_list))else:continueGini = Gini - Best_Gini# print("最优切分点：", BestSplit_Point)return BestSplit_Point, BestSplit_Positiondef get_cart_bincut(data, var, target, leaf_stop_percent=0.05):""" 计算最优分箱切分点Args:data: DataFrame，拟操作的数据集var: String，拟分箱的连续型变量名称target: String，Y列名称leaf_stop_percent: 叶子节点占比，作为停止条件，默认5%Returns:best_bincut: 最优的切分点列表，List"""min_sample = len(data) * leaf_stop_percentbest_bincut = []def cutting_data(data, var, target, min_sample, best_bincut):split_point, position = get_cart_split_point(data, var, target, min_sample)if split_point != -99999:best_bincut.append(split_point)# 根据最优切分点切分数据集，并对切分后的数据集递归计算切分点，直到满足停止条件# print("本次分箱的值域范围为{0} ~ {1}".format(data[var].min(), data[var].max()))left = data[data[var] < split_point]right = data[data[var] > split_point]# 当切分后的数据集仍大于最小数据样本要求，则继续切分if len(left) >= min_sample and position not in [0.0, 1.0]:cutting_data(left, var, target, min_sample, best_bincut)else:passif len(right) >= min_sample and position not in [0.0, 1.0]:cutting_data(right, var, target, min_sample, best_bincut)else:passreturn best_bincutbest_bincut = cutting_data(data, var, target, min_sample, best_bincut)# 把切分点补上头尾best_bincut.append(data[var].min())best_bincut.append(data[var].max())best_bincut_set = set(best_bincut)best_bincut = list(best_bincut_set)best_bincut.remove(data[var].min())best_bincut.append(data[var].min()-1)# 排序切分点best_bincut.sort()return best_bincut

03 基于卡方检验的最优分箱代码实现

基于卡方检验的连续变量最优分箱，实现步骤如下：
1，给定连续变量 V，对V中的值进行排序，然后每个元素值单独一组，完成初始化阶段；
2，对相邻的组，两两计算卡方值；
3，合并卡方值最小的两组；
4，递归迭代步骤2-3，直到满足停止条件。（一般是卡方值都高于设定的阈值，或者达到最大分组数等等）

def calculate_chi(freq_array):""" 计算卡方值Args:freq_array: Array，待计算卡方值的二维数组，频数统计结果Returns:卡方值，float"""# 检查是否为二维数组assert(freq_array.ndim==2)# 计算每列的频数之和col_nums = freq_array.sum(axis=0)# 计算每行的频数之和row_nums = freq_array.sum(axis=1)# 计算总频数nums = freq_array.sum()# 计算期望频数E_nums = np.ones(freq_array.shape) * col_nums / numsE_nums = (E_nums.T * row_nums).T# 计算卡方值tmp_v = (freq_array - E_nums)**2 / E_nums# 如果期望频数为0，则计算结果记为0tmp_v[E_nums==0] = 0chi_v = tmp_v.sum()return chi_vdef get_chimerge_bincut(data, var, target, max_group=None, chi_threshold=None):""" 计算卡方分箱的最优分箱点Args:data: DataFrame，待计算卡方分箱最优切分点列表的数据集var: 待计算的连续型变量名称target: 待计算的目标列Y的名称max_group: 最大的分箱数量（因为卡方分箱实际上是合并箱体的过程，需要限制下最大可以保留的分箱数量）chi_threshold: 卡方阈值，如果没有指定max_group，我们默认选择类别数量-1，置信度95%来设置阈值如果不知道卡方阈值怎么取，可以生成卡方表来看看，代码如下：  import pandas as pdimport numpy as npfrom scipy.stats import chi2p = [0.995, 0.99, 0.975, 0.95, 0.9, 0.5, 0.1, 0.05, 0.025, 0.01, 0.005]pd.DataFrame(np.array([chi2.isf(p, df=i) for i in range(1,10)]), columns=p, index=list(range(1,10)))Returns:最优切分点列表，List"""freq_df = pd.crosstab(index=data[var], columns=data[target])# 转化为二维数组freq_array = freq_df.values# 初始化箱体，每个元素单独一组best_bincut = freq_df.index.values# 初始化阈值 chi_threshold，如果没有指定 chi_threshold，则默认选择target数量-1，置信度95%来设置阈值if max_group is None:if chi_threshold is None:chi_threshold = chi2.isf(0.05, df = freq_array.shape[-1])# 开始迭代while True:min_chi = Nonemin_idx = Nonefor i in range(len(freq_array) - 1):# 两两计算相邻两组的卡方值，得到最小卡方值的两组v = calculate_chi(freq_array[i: i+2])if min_chi is None or min_chi > v:min_chi = vmin_idx = i# 是否继续迭代条件判断# 条件1：当前箱体数仍大于 最大分箱数量阈值# 条件2：当前最小卡方值仍小于制定卡方阈值if (max_group is not None and max_group < len(freq_array)) or (chi_threshold is not None and min_chi < chi_threshold):tmp = freq_array[min_idx] + freq_array[min_idx+1]freq_array[min_idx] = tmpfreq_array = np.delete(freq_array, min_idx+1, 0)best_bincut = np.delete(best_bincut, min_idx+1, 0)else:break# 把切分点补上头尾best_bincut = best_bincut.tolist()best_bincut.append(data[var].min())best_bincut.append(data[var].max())best_bincut_set = set(best_bincut)best_bincut = list(best_bincut_set)best_bincut.remove(data[var].min())best_bincut.append(data[var].min()-1)# 排序切分点best_bincut.sort()return best_bincut

04 基于最优KS的最优分箱代码实现

基于最优KS的连续变量最优分箱，实现步骤如下：
1，给定连续变量 V，对V中的值进行排序；
2，每一个元素值就是一个计算点，对应上图中的bin0～9；
3，计算出KS最大的那个元素，作为最优划分点，将变量划分成两部分D1和D2；
4，递归迭代步骤3，计算由步骤3中产生的数据集D1 D2的划分点，直到满足停止条件。（一般是分箱数量达到某个阈值，或者是KS值小于某个阈值）

def get_maxks_split_point(data, var, target, min_sample=0.05):""" 计算KS值Args:data: DataFrame，待计算卡方分箱最优切分点列表的数据集var: 待计算的连续型变量名称target: 待计算的目标列Y的名称min_sample: int，分箱的最小数据样本，也就是数据量至少达到多少才需要去分箱，一般作用在开头或者结尾处的分箱点Returns:ks_v: KS值，floatBestSplit_Point: 返回本次迭代的最优划分点，floatBestSplit_Position: 返回最优划分点的位置，最左边为0，最右边为1，float"""if len(data) < min_sample:ks_v, BestSplit_Point, BestSplit_Position = 0, -9999, 0.0else:freq_df = pd.crosstab(index=data[var], columns=data[target])freq_array = freq_df.valuesif freq_array.shape[1] == 1: # 如果某一组只有一个枚举值，如0或1，则数组形状会有问题，跳出本次计算# tt = np.zeros(freq_array.shape).T# freq_array = np.insert(freq_array, 0, values=tt, axis=1)ks_v, BestSplit_Point, BestSplit_Position = 0, -99999, 0.0else:bincut = freq_df.index.valuestmp = freq_array.cumsum(axis=0)/(np.ones(freq_array.shape) * freq_array.sum(axis=0).T)tmp_abs = abs(tmp.T[0] - tmp.T[1])ks_v = tmp_abs.max()BestSplit_Point = bincut[tmp_abs.tolist().index(ks_v)]BestSplit_Position = tmp_abs.tolist().index(ks_v)/max(len(bincut) - 1, 1)return ks_v, BestSplit_Point, BestSplit_Positiondef get_bestks_bincut(data, var, target, leaf_stop_percent=0.05):""" 计算最优分箱切分点Args:data: DataFrame，拟操作的数据集var: String，拟分箱的连续型变量名称target: String，Y列名称leaf_stop_percent: 叶子节点占比，作为停止条件，默认5%Returns:best_bincut: 最优的切分点列表，List"""min_sample = len(data) * leaf_stop_percentbest_bincut = []def cutting_data(data, var, target, min_sample, best_bincut):ks, split_point, position = get_maxks_split_point(data, var, target, min_sample)if split_point != -99999:best_bincut.append(split_point)# 根据最优切分点切分数据集，并对切分后的数据集递归计算切分点，直到满足停止条件# print("本次分箱的值域范围为{0} ~ {1}".format(data[var].min(), data[var].max()))left = data[data[var] < split_point]right = data[data[var] > split_point]# 当切分后的数据集仍大于最小数据样本要求，则继续切分if len(left) >= min_sample and position not in [0.0, 1.0]:cutting_data(left, var, target, min_sample, best_bincut)else:passif len(right) >= min_sample and position not in [0.0, 1.0]:cutting_data(right, var, target, min_sample, best_bincut)else:passreturn best_bincutbest_bincut = cutting_data(data, var, target, min_sample, best_bincut)# 把切分点补上头尾best_bincut.append(data[var].min())best_bincut.append(data[var].max())best_bincut_set = set(best_bincut)best_bincut = list(best_bincut_set)best_bincut.remove(data[var].min())best_bincut.append(data[var].min()-1)# 排序切分点best_bincut.sort()return best_bincut

05 测试效果与小节

好了，我们也把上面的3种连续变量分箱的方法用Python实现了一下，马上来测试下效果吧。

df['age_bins1'] = pd.cut(df['age'], bins=get_cart_bincut(df, 'age', 'target'))
df['age_bins2'] = pd.cut(df['age'], bins=get_chimerge_bincut(df, 'age', 'target'))
df['age_bins3'] = pd.cut(df['age'], bins=get_bestks_bincut(df, 'age', 'target'))
print("变量 age 的分箱结果如下：")
print("age_cart_bins:", get_cart_bincut(df, 'age', 'target'))
print("age_chimerge_bins:", get_chimerge_bincut(df, 'age', 'target'))
print("age_bestks_bins:", get_bestks_bincut(df, 'age', 'target'))
print("IV值如下：")
print("age:", iv_count(df, 'age', 'target'))
print("age_cart_bins:", iv_count(df, 'age_bins1', 'target'))
print("age_chimerge_bins:", iv_count(df, 'age_bins2', 'target'))
print("age_bestks_bins:", iv_count(df, 'age_bins3', 'target'))df['income_bins1'] = pd.cut(df['income'], bins=get_cart_bincut(df, 'income', 'target'))
df['income_bins2'] = pd.cut(df['income'], bins=get_chimerge_bincut(df, 'income', 'target'))
df['income_bins3'] = pd.cut(df['income'], bins=get_bestks_bincut(df, 'income', 'target'))
print("变量 income 的分箱结果如下：")
print("income_cart_bins:", get_cart_bincut(df, 'income', 'target'))
print("income_chimerge_bins:", get_chimerge_bincut(df, 'income', 'target'))
print("income_bestks_bins:", get_bestks_bincut(df, 'income', 'target'))
print("IV值如下：")
print("income:", iv_count(df, 'income', 'target'))
print("income_cart_bins:", iv_count(df, 'income_bins1', 'target'))
print("income_chimerge_bins:", iv_count(df, 'income_bins2', 'target'))
print("income_bestks_bins:", iv_count(df, 'income_bins3', 'target'))

我们从中可以看到，3种不同的分箱方法效果还是有些不同的，但有一个共通点就是IV值都比分箱前要小，毕竟为了效率牺牲一些“IV”也是合理的。而在实际建模中，我一般都是直接用3种方法，选择最优分箱效果的那个。
以上是相对比较简单的实现，也欢迎大家试用下，有什么问题可以随机反馈～另外如果大家喜欢这篇文章的话，欢迎点赞转发哦，谢谢！

Reference

https://blog.csdn.net/xgxyxs/article/details/90413036
https://zhuanlan.zhihu.com/p/44943177
https://blog.csdn.net/hxcaifly/article/details/84593770
https://blog.csdn.net/haoxun12/article/details/105301414/
https://www.bilibili.com/read/cv12971807