网站哪个公司做的比较好/谷歌推广运营

本周主要进行了支持向量机的相关知识点的串讲。

· 首先理解支持向量机的基本概念

o 取一条直线将目标物体进行区分，意味着直线附近的点会影响算法的结果，与线性回归相比简化了数据的复杂度。

o 用到线性代数模型y=mx+b 假设在目标点之间有一条线，距离此线的上下垂直距离，假设分别为d1 与d2，那么目标函数为wx+b=0，此条线以上wx+b=c，此条线以下wx+b=-c，有时候为了计算简便，可假设c为1与-1

· 相关的数学原理

o 在上面的线，用w与b向量构建一个函数，w(T)X1 + b =1 （假设c为1），下面的线则为w(T)X2 + b =-1，两相减得到w(T)(X1-X2)=2，经过一系列的数学演算，得到d1+d2=2/|w|(表示为w的模)，如图所示：

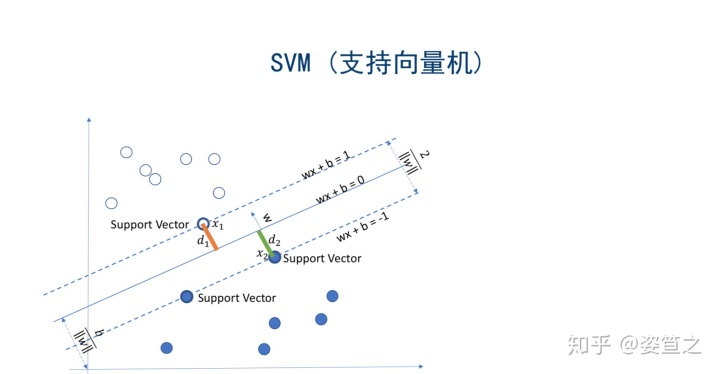
· 如何找到一个好的分割线

· 带松弛变量的SVM数学模型

o 最大的区别在于，此数学模型考虑了松弛变量C，某种程度上加大了模型的松弛程度，可以让模型最大范围内容忍两条直线的跨度。

· 如何处理异常值

o 放松限制：此方法容忍两线之间的距离以确保结果的最优化。

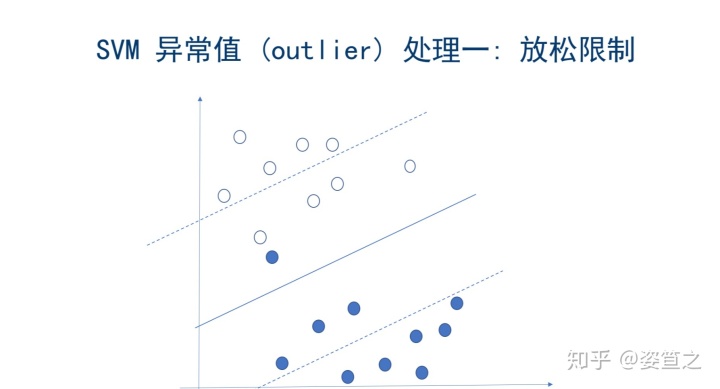
o 不放松限制：此方法严格的控制两线之间的距离，不允许C系数的最大化。

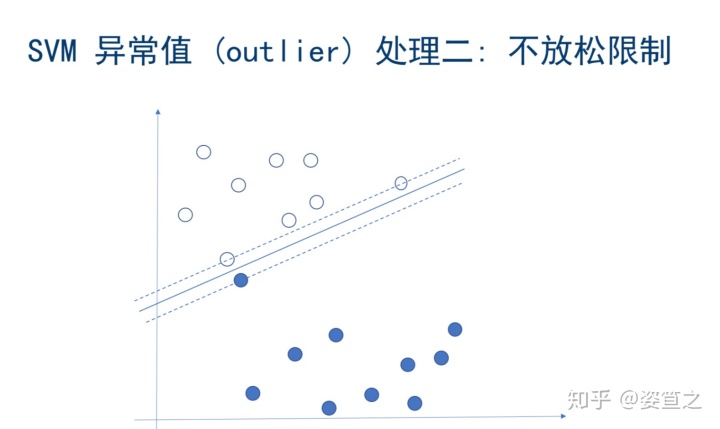
o 必须放松限制：此情况比较复杂，需要具体问题具体分析。

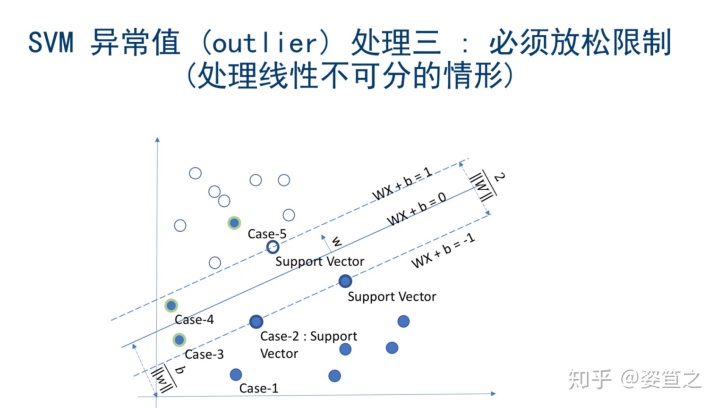
· 支持向量机的优缺点

o 优点：模型只需要保存支持向量, 模型占用内存少, 预测快.

分类只取决于支持向量, 适合数据的维度高的情况, 例如DNA数据

o 缺点：训练的时间复杂度为 [ 3]O[N3] 或者至少 [ 2]O[N2], 当数据量巨大时候不合适使用.

需要做调参 C 当数据量大时非常耗时间.

总结：由于是初学课程，很多算法的推岛过程不熟悉，希望今后可以循序渐进，一回生二回熟。