把收藏夹网站设置成主业怎么做/南宁seo教程
这篇博客记录第5天刷题的思路和收获。
23.合并K个升序链表
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:
输入:lists = [[1,4,5],[1,3,4],[2,6]] 输出:[1,1,2,3,4,4,5,6] 解释:链表数组如下: [
1->4->5,
1->3->4,
2->6 ]
将它们合并到一个有序链表中得到。 1->1->2->3->4->4->5->6示例 2:
输入:lists = [] 输出:[]
示例 3:
输入:lists = [[]] 输出:[]
提示:
k == lists.length 0 <= k <= 10^4 0 <= lists[i].length <= 500 -10^4 <= lists[i][j] <= 10^4 lists[i] 按 升序 排列 lists[i].length 的总和不超过 10^4
分析:这题乍一看和21. 合并两个有序链表的题相似,但却是hard级别,难就难在对于两个链表节点可以比较大小,而对于链表数组的多个链表节点很难排序比较大小。这题可以用分治来做,链表两两合并不断比较大小。但我还不大会分治算法,有空学一下。下面的分析直接照搬评论区大佬的思路和代码。
这里可以利用C++中的STL priority_queue,定义一个最小堆有限队列,存放所有链表的头节点。然后出队当前最小节点连上链表,同时让出队节点的下一个入队,再出队当前优先队列中最小的,直到队列为空。
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergeKLists(vector<ListNode*>& lists) {ListNode head(0);//定义节点大小比较的Functional(类比greater<int>)auto comp = [](ListNode* const &a, ListNode* const &b) {return a->val > b->val; //lambda表达式类型是全局唯一,只能用auto,传类型的时用decltype获得};//定义最小堆优先队列,存放所有链表的头节点priority_queue<ListNode*, vector<ListNode*>, decltype(comp)> q(comp);for (auto &h : lists) {if (h != nullptr)q.push(h);}auto p = &head;while(!q.empty()) { p->next = q.top(); //出队当前最小节点,连上链表p = p->next;q.pop(); if (p->next != nullptr)q.push(p->next); //让出队节点的下一个入队}return head.next;}
};
参考:
[1] c++优先队列(priority_queue)用法详解
[2] auto与decltype关键字
26. 删除排序数组中的重复项
给定一个排序数组,你需要在 原地 删除重复出现的元素,使得每个元素只出现一次,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
示例 1:
给定数组 nums = [1,1,2],
函数应该返回新的长度 2, 并且原数组 nums 的前两个元素被修改为 1, 2。
你不需要考虑数组中超出新长度后面的元素。
示例 2:
给定 nums = [0,0,1,1,1,2,2,3,3,4],
函数应该返回新的长度 5, 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。
你不需要考虑数组中超出新长度后面的元素。
分析:这个问题可以用双指针求解,代码也是照搬别人的,非常巧妙,(我什么时候能写出这种代码啊[捂脸])具体分析见c++代码注释,应该能看懂。
class Solution {
public:int removeDuplicates(vector<int>& nums) {if (nums.size() < 2) return nums.size();int i = 0, j = 1;//定义前后双指针,指向两值不等则同时移动,while (j < nums.size()) {if(nums[i] != nums[j]) {nums[++i] = nums[j]; //若指针间隔=1相当于未赋值,间隔>1则前指针将较大值赋给后指针的前一个元素}j++; //指向两个值相等则不赋值,只移动前面指针}return ++i; //最终取截至后指针前一个下标的不重复数组}
};
33. 搜索旋转排序数组
升序排列的整数数组 nums 在预先未知的某个点上进行了旋转(例如, [0,1,2,4,5,6,7] 经旋转后可能变为 [4,5,6,7,0,1,2] )。
请你在数组中搜索 target ,如果数组中存在这个目标值,则返回它的索引,否则返回 -1 。
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0 输出:4
示例 2:
输入:nums = [4,5,6,7,0,1,2], target = 3 输出:-1
示例 3:
输入:nums = [1], target = 0 输出:-1
提示:
1 <= nums.length <= 5000 -10^4 <= nums[i] <= 10^4 nums 中的每个值都 独一无二 nums 肯定会在某个点上旋转 -10^4 <= target <= 10^4
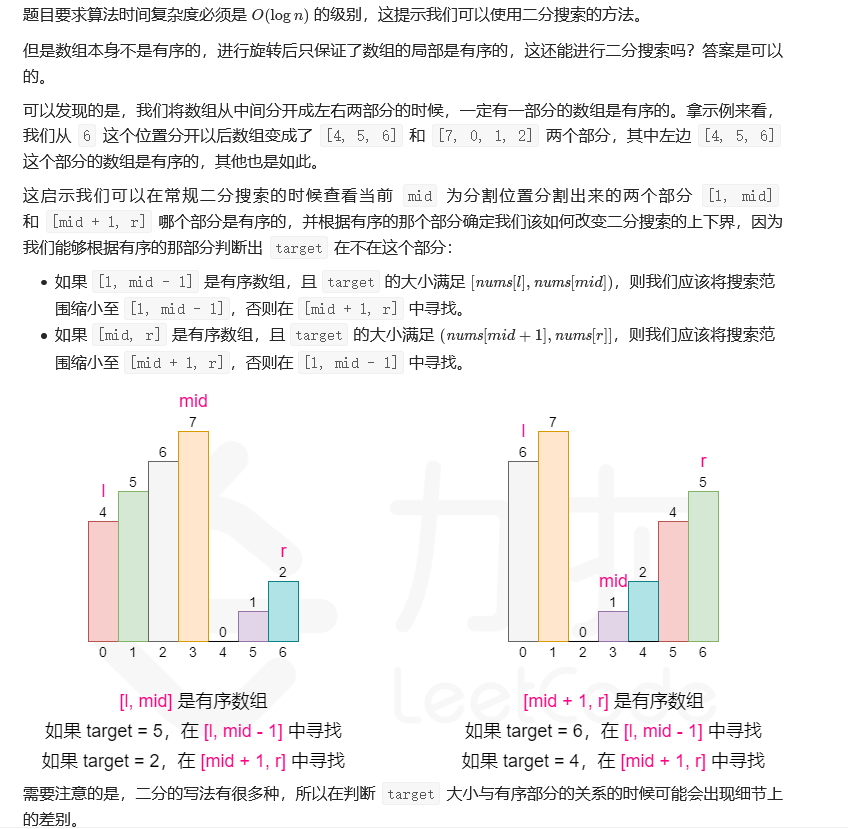
在此说一点我的理解:对于旋转的排序数组,是无序的,但target的左右数组都是有序的。搜索target时,除非当前指针mid正好指向target,否则要么只有左侧数组[0,mid−1][0,mid-1][0,mid−1]有序,要么只有右侧数组[mid,n−1][mid,n-1][mid,n−1]有序。那么如何利用二分法搜索呢?每次我们判断target是否在有序数组内,在的话就将其作为搜索范围,不在的话就将无序数组作为搜素范围。照搬官方解答如下:
class Solution {
public:int search(vector<int>& nums, int target) {int n = nums.size();if (!n) return -1;if (n == 1)return nums[0] == target ? 0 : -1;int l = 0, r = n-1;while (l <= r) {int mid = (l + r) / 2;if (nums[mid] == target) return mid;if (nums[0] <= nums[mid]) { //左边[0,mid]有序数组if (nums[0] <= target && target < nums[mid]) //target在有序数组内r = mid - 1;elsel = mid + 1;}else { //左侧无序,则右侧[mid+1, n-1]有序if (nums[mid] < target && target <= nums[n-1]) //target在有序数组内l = mid + 1;elser = mid - 1;}}return -1;}
};
注意:二分法搜素对于下标是否越界,判断是否在某个范围要不要加等号(开区间or 闭区间)非常tricky,比如下面的报错就是对于元素仅有2个的小数组发生了mid下标越界,因为我使用了如下语句来判断左边[0,mid-1]是否为有序数组,初始情况下 l=0,r=1l=0, r=1l=0,r=1所以 mid=0mid=0mid=0,mid−1mid-1mid−1就越界了,所以不应该在程序里使用 mid−1mid-1mid−1 和 mid+1mid+1mid+1 等语句。
if (nums[0] <= nums[mid-1])nums[0] <= target && target <= nums[mid-1]
二分法查找
这里额外补充一点二分法查找,直接引用LeetCode评论区题解,感谢!
作者:yuan-chu-de-suan-fa-xiao-wu
链接:https://leetcode-cn.com/problems/search-in-rotated-sorted-array/solution/yi-wen-dai-ni-shua-bian-er-fen-cha-zhao-dtadq/
来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
二分查找的执行过程如下:
1.从已经排好序的数组或区间中,取出中间位置的元素,将其与我们的目标值进行比较,判断是否相等,如果相等则返回。
2.如果 nums[mid] 和 target 不相等,则对 nums[mid] 和 target 值进行比较大小,通过比较结果决定是从 mid的左半部分还是右半部分继续搜索。如果 target > nums[mid] 则右半区间继续进行搜索,即 left = mid + 1; 若 target < nums[mid] 则在左半区间继续进行搜索,即 right = mid -1;
动图解析二分查找
 下面我们来看一下二分查找的代码,可以认真思考一下 if 语句的条件,每个都没有简写。
下面我们来看一下二分查找的代码,可以认真思考一下 if 语句的条件,每个都没有简写。
int binarySearch(int nums[],int target,int left, int right) {//这里需要注意,循环条件while (left <= right) {//这里需要注意,计算midint mid = left + ((right - left) >> 1); //left + (right - left)/2if (nums[mid] == target) {return mid;}else if (nums[mid] < target) {//这里需要注意,移动左指针left = mid + 1;}else if (nums[mid] > target) {//这里需要注意,移动右指针right = mid - 1;}}//没有找到该元素,返回 -1return -1;}
二分查找的思路及代码已经理解了,那么我们来看一下实现时容易出错的地方
1.计算 mid 时 ,不能使用 (left + right )/ 2,否则有可能会导致溢出。
2.while (left < = right) { } 注意括号内为 left <= right ,而不是 left < right。
3.left = mid + 1,right = mid - 1 而不是 left = mid 和 right = mid。