界面设计心得/青岛网站优化
一、傅里叶变换 (FT)
二、傅里叶变换(FT)的缺点与短时傅里叶变换(STFT)
三、短时傅里叶变换(STFT)的缺点与连续小波变换(CWT)
四、连续小波变换(CWT)的缺点与离散小波变换(DWT)
源代码:1368069096/From_FT_to_WT_examples-
四、连续小波变换(CWT)的缺点与离散小波变换(DWT)
1、连续小波变换(CWT)的缺点
在上一篇文章(https://zhuanlan.zhihu.com/p/68323379)中我们讲解了 CWT可以实现动态分辨率的时频分析。CWT公式为:
但是在第二篇文章(https://zhuanlan.zhihu.com/p/66246381)中我们讲过,实际采样信号往往具有两个特点:1、离散性,就是采集数据不连续,很容易理解,采集信号肯定是一个一个数据采集的;2、有限性,虽然理想的CWT是从
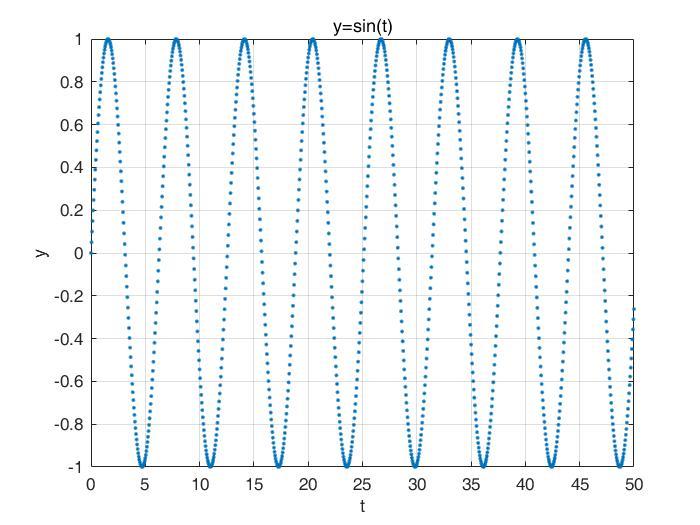
所以,由于CWT需要一个连续信号,但是实际采样信号往往是离散的,我们无法直接对实际信号进行CWT。
或许你想,我们对实际采样信号进行插值连续化不就可以使得其连续了吗?
是的。将实际采样信号插值连续化之后,我们——人,是可对它进行CWT的。
但是,我们也都知道,我们的帮手——计算机,是无法处理连续问题的。计算机只能处理离散问题。如果计算机要进行CWT,就意味着需要计算机做无穷次运算,计算机计算能力再强也是做不到的。
因此,为了使得计算机可以进行小波变换,我们需要引入离散小波变换(DWT)。
2、离散小波变换(DWT)的Mallet算法
DWT有很多种实现方式,我们在这里介绍Mallet算法,它是DWT的以一种经典的快速算法,也比较易懂。
我们首先来回顾一下上一篇文章讲过的动态分辨率图:高频部分,窄窗,高的时域分辨率,低的频域分辨率;低频部分,宽窗,低的时域分辨率,高的频域分辨率。
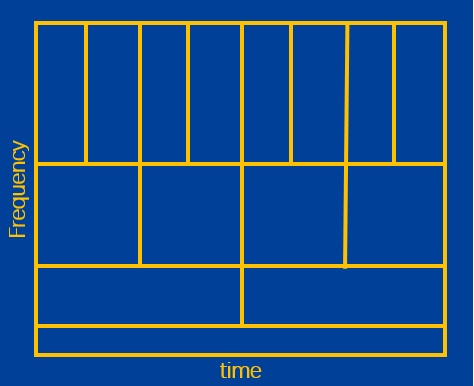
我们是利用小波母函数的挤压和拉伸来实现动态分辨率的:
当小波母函数被挤压的时候,频率就高,此时窗子窄,时域分辨率就好,根据海森堡测不准原理,频域分辨率就差;
当小波母函数被拉伸的时候,频率就低,此时窗子宽,时域分辨率就差,根据海森堡测不准原理,频域分辨率就好。
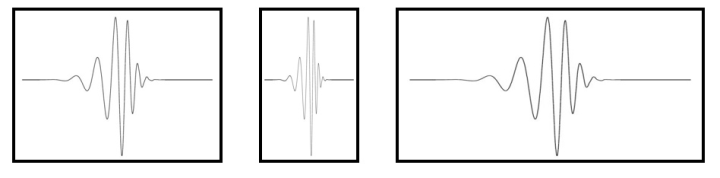
也就是说,我们控制的是不同频率对应的窗长(即时域分辨率),频率分辨率是通过海森堡测不准原理得到的,从而达到了动态分辨率。
那么,如果我们这次不控制窗长(即时域分辨率),转而控制频域分辨率,能否达到动态分辨率呢?
答案是可以,这就是Mallet算法要解决的问题。
半子带滤波
我们知道,小波母函数本质上是一种带通滤波器。那么,假设可以通过小波母函数构造得到两个滤波器(至于怎么得到后续会介绍一下),包括一个高通滤波器和一个低通滤波器。
假设信号中的最高频率为
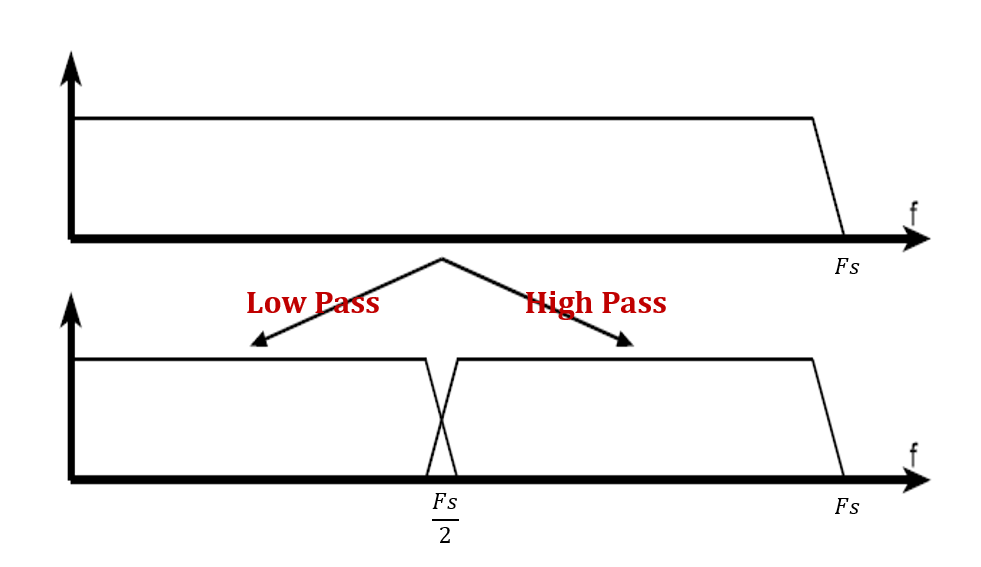
我们将这个过程称为一次半子带滤波。
下采样与上采样
我们定义一个N倍下采样过程:将采样点N倍稀释。如下,就是一个2倍下采样过程,将采样点稀释2倍,即:每2个点采样数据点,就去除一个点。
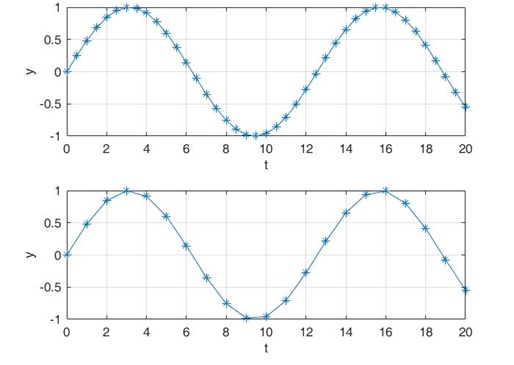
N倍上采样过程:将采样点数量增加N倍。一般通过补0,或者插值的方法实现上采样。
离散小波分解
我们将一次半子带滤波+一次2倍下采样称为一层小波分解。如下图所示,图中的“箭头+2”表示一次2倍下采样。
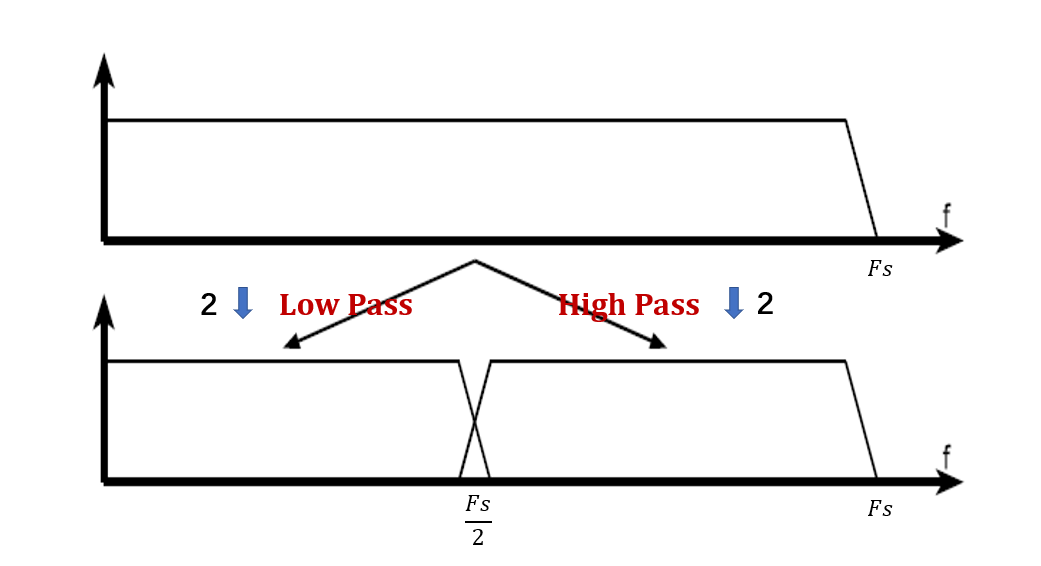
假设原采样信号有
经过一次高通滤波后,得到了
经过一次低通滤波后,得到了
也就是说,经过一层小波分解的信号,它的总长度加起来,还是
现在,我们已经对
那么,我们保持
这个过程被称为第2层小波分解。我们验证一下,经过2层小波分解的信号,它的总长度加起来,还是
依此类推,我们可以进行第三层,第四层小波分解,如图所示,直到第
因此,小波分解的原始信号个数一般也需要是2的幂次。不过,在各种数学计算软件里,如果输入不是2的幂次,它会自动帮你补零到2的幂次。
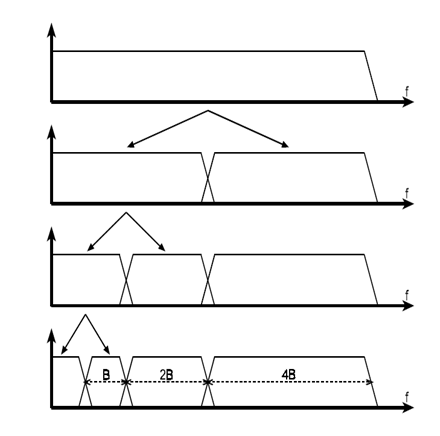
我们取4层小波分解的结果来看一下。
在频域上,我们得到的是
在时域上,由于不断的2倍下采样,不断地丢弃数据,所以最后一层分解得到的
那么,我们得到的分辨率就是这样子的:
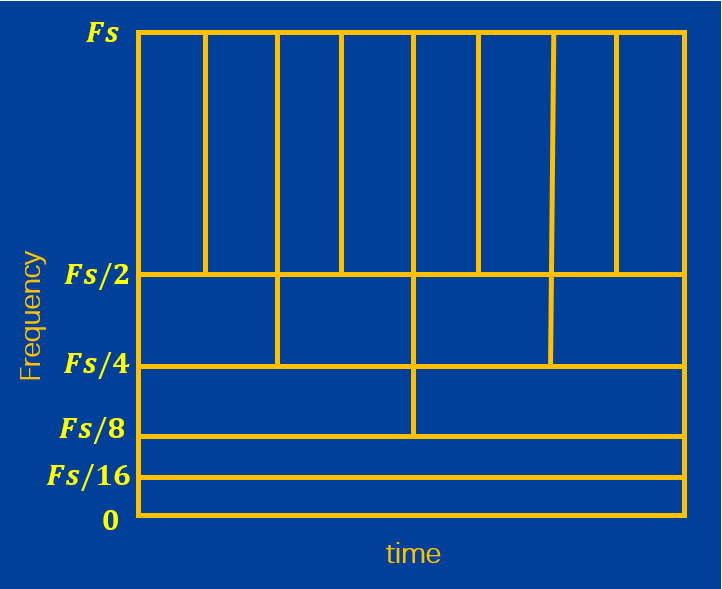
这,不就是上一篇文章我们讲过的小波变换得到的动态分辨率吗?
是的!这就是离散小波变换的快速算法之一——Mallet算法,通过不断的半子带滤波和下采样,控制不同频率成分的频域分辨率,进而达到动态分辨率。
最后,用一张比较经典的图,再来演示一下小波分解的过程。
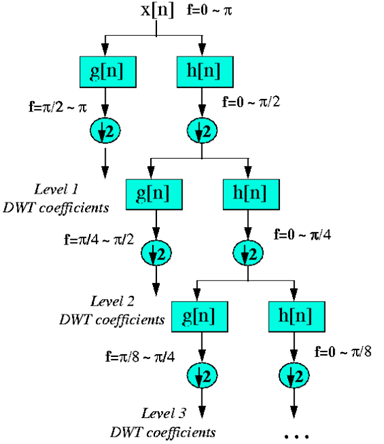
再来举个例子形象地说明一下DWT的使用吧。
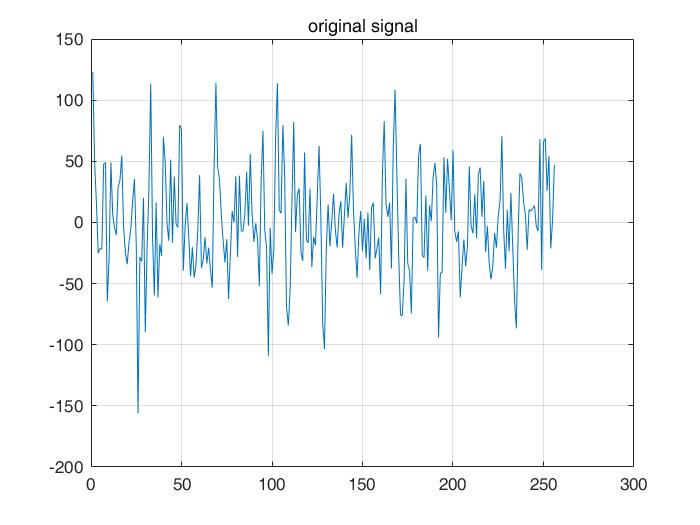
希望对于一个采样率为1000HZ的非稳态信号进行小波分解,下图为包含了256个采样点(即256ms)的原始采样信号。
1、首先,选择小波分解的层次。
可以根据对最低频率区间的要求来选择小波分解的层数。比如,我之前做项目的时候,采样率为1000HZ,那么信号的最高频率为
2、接下来,进行5层小波分解,得到小波分解系数。
如下图中,图1依然是原始采样信号 ,图2到图6为第1层到第5层小波分解的高频系数,图7为第5层小波分解的低频系数。如图所示,这些小波分解系数对应着不同的频率区间。
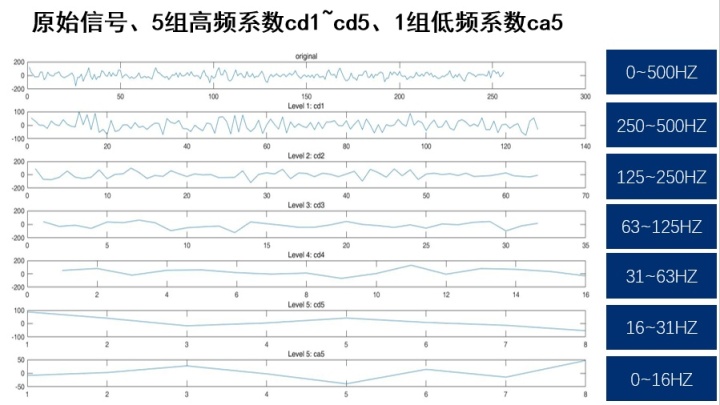
这就是DWT了,又称为小波分解。
这里提一下,小波分解是可逆的,即可以通过不同频率区间的小波分解系数进行重构,得到不同频率区间的重构信号。
3、所以,最后,进行小波重构,得到重构信号。
如下图中,图1依然是原始采样信号,图2到图7为通过不同频率区间的小波系数进行重构,得到的重构信号。将图2到图7加起来就可以得到重构原始信号,其和原始采样信号的误差称为重构误差。
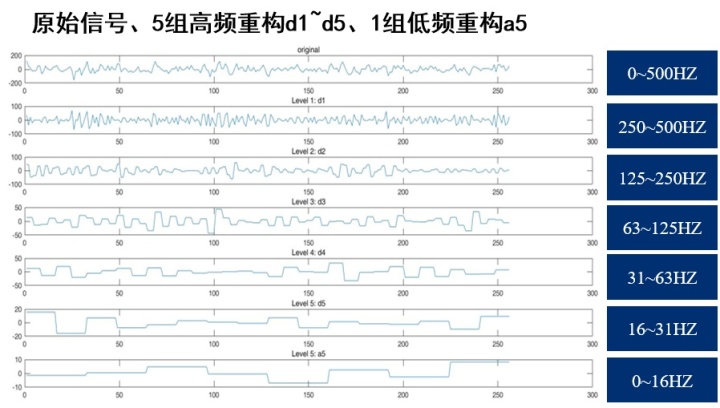
3、Mallet算法背后的数学原理简介
这一部分主要是为了解答上一部分中的两个问题。
1、在上一部分,我们“假设可以通过小波母函数构造得到两个滤波器”,那么,怎么得到刚好可以具有以上特性的滤波器呢?
2、在上一部分,我们将小波分解之后的结果称为“系数”,那么,为什么称为系数呢?
先说一下,这部分我不是弄得非常懂,毕竟我只是个做工程的本科生,不是做数学的大佬。我凭自己的理解写一写大概,并推荐了两篇个人觉得讲得很好的回答。
我们用Haar小波做例子。
首先,介绍一个Haar尺度函数(又称为父小波),记为
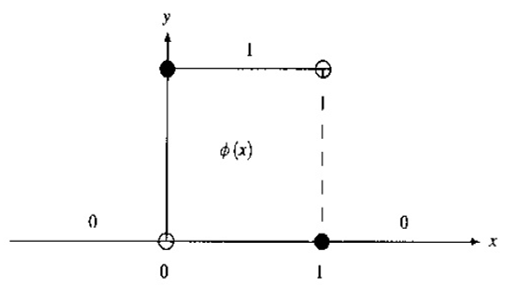
通过Haar尺度函数
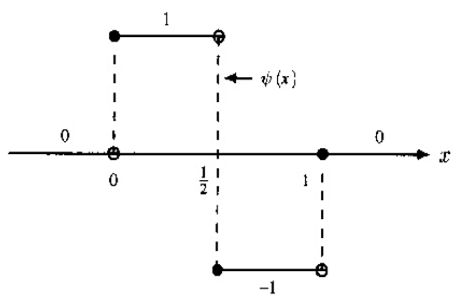
现在,对于一个
从直观上看,Haar尺度函数只是一条线,而Haar母小波则是一个波。所以,Haar母小波所能表示出来的信息应该更加细致。因此,
我们将
所以,DWT的滤波功能,是通过利用尺度函数和母小波重构信号,获取重构系数来获得的,这已经定性地解决了本部分提出的问题。
关于DWT背后的数学原理,推荐两篇回答:
关右:通过Haar小波认识离散小波变换zhuanlan.zhihu.com
最后,由于DWT分解得到的是高频系数和低频系数,也就是用尺度函数以及母小波表示原信号的时候的一些重构系数,所以通过重构系数可以重构该信号,这被称为小波分解的重构。这也说明了小波分解是可逆的。
1335:从傅里叶变换进阶到小波变换(一)zhuanlan.zhihu.comhttp://feihu.eng.ua.edu/NSF_TUES/w7_2.pdf(参考资料)
