(一)图与网络的基本概念
一、无向图
含有的元素为顶点,弧和权重,但是没有方向
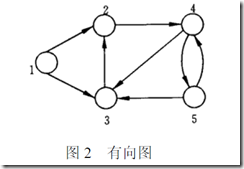
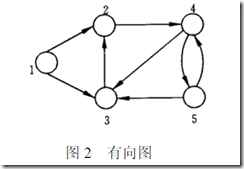
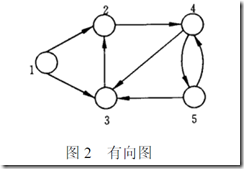
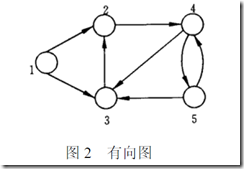
二、有向图
含有的元素为顶点,弧和权重,弧具有方向。
三、有限图、无限图
顶点和边有限就是有限图,否则就是无限图。
四、简单图
既没有环,也没有两条边连接同一对顶点的图
五、完全图、二分图
每一对不同的顶点都有一条边相连的简单图称为完全图。

六、子图
就是被包含的图
七、顶点的度
就是顶点连接了几条边。
性质:1、全部顶点的度相加为偶数
2、 任意一个图的奇顶点的个数为偶数。
(二)图与网络的数据结构
一、邻接矩阵表示法
1、定义:
就是0-1矩阵,如果元素cij为“1”表示弧从第i个到第j个点,为“0”的话表示没有。如果是无向图则必定cij=cji。
2、一个demo:

3、缺点
浪费大量的空间
二、关联矩阵表示法
1、定义
在关联矩阵中,每行对应图的一个节点,每列对应图的一条弧。如果元素为“1”为一条弧的起点,元素为“-1”是一条弧的终点,元素为“0”与弧没有关联。
2、缺点:
浪费大量的弓箭
3、一个demo

三、弧表表示法
1、定义:
上面两种方法都是以点优先,这种方法以边优先,记录下来每个边的起点,终点和权重。
2、一个demo

四、邻接表表示法
1、定义
就是用一个单向链表存储所有的顶点,然后每个顶点又是一个单向链表的头指针, 引导着每个由它出发的弧。
2、一个demo
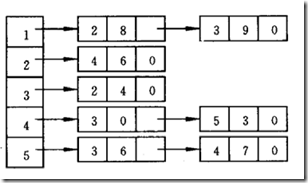
五、星形表示法
1、前向星形表示法
(1)定义:
定义2个数组,一个数组记录边信息的数组,跟换标表示法类似,然后还有一个数组记录每个出弧的起始地址编号
(2)demo
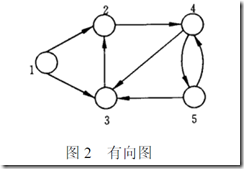
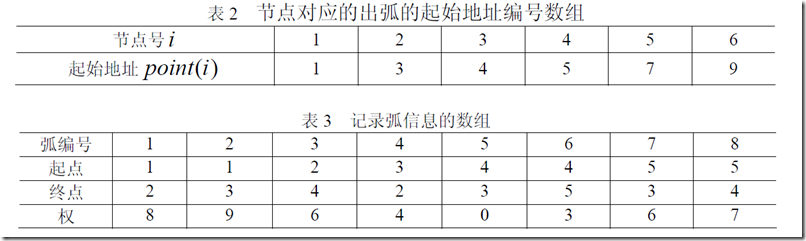
(3)性质
a、在point数组中,节点号比图的顶点多一个,一定要有point(1)=1,point(n)=m+1,
b、对于一个节点i,其对应的弧的信息数组的位置区间为![]()
如果![]() ,则没有出弧。
,则没有出弧。
(4)评价
能快速检索每个节点的所有出弧,但是没有办法快速检索每个节点的所有入弧。
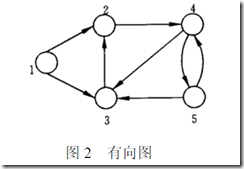
2、后向星形表示法
(1)定义:
定义2个数组,一个数组记录边信息的数组,跟换标表示法类似,然后还有一个数组记录每个出弧的起始地址编号,但是是记录从终点到顶点。
(2)demo
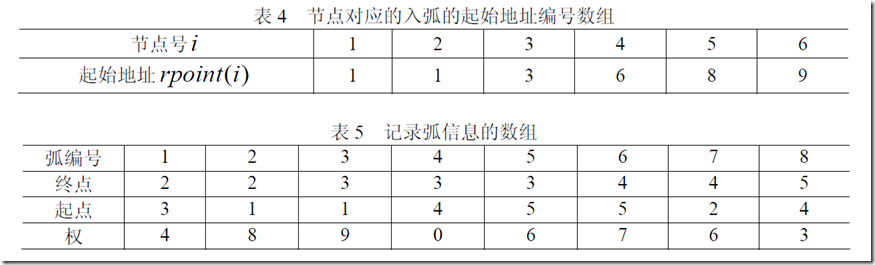
3、双星型表示法
(1)加前向星形表示法的基础上,再加上一个正向弧对应的编号即可
(2)demo

(三)应用——最短路问题
一、从指定1点到其他所有点的最短路径(无向图)
1、算法

例子:

![]()
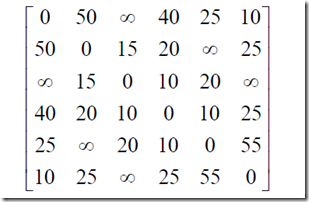
MATLAB编程求解
clc,clear; a=zeros(6); a(1,2)=50;a(1,4)=40;a(1,5)=25;a(1,6)=10; a(2,3)=15;a(2,4)=20;a(2,6)=25; a(3,4)=10;a(3,5)=20; a(4,5)=10;a(4,6)=25; a(5,6)=55; a=a+a'; ll=find(a==0); a(ll)=inf; pb(1:length(a))=0;pb(1)=1;index1=1;index2=ones(1,length(a)); d(1:length(a))=inf;d(1)=0;temp=1; %pb是用来标记是否走过(每次取最小路径所到达的地点),index1是指遍历地点的路径,index2是指到底地点前一个地点,然后从index1
%中找到它的最短路径。d是记录从1到每个地点的最短路径。 while sum(pb)<length(a)tb=find(pb==0); %取出没走过的点d(tb)=min(d(tb),d(temp)+a(temp,tb)); %用上一次的最小值,和前者与这次的步径相加相比较,得出当前的最短路径tmpb=find(d(tb)==min(d(tb))); temp=tb(tmpb(1)); %取出目前最短的路径,然后选定为下一个起点pb(temp)=1;index1=[index1,temp];temp2=find(d(index1)==d(temp)-a(temp,index1)); %确定到目前点之前一点,确定的方法是用到此点的最短路径减去这次走的路径与之前的最短路径作比较。(按
%index1顺序),这样就可以得到上次来到此地的点。index2(temp)=index1(temp2(1)); end d,index1,index2
二、两个指定顶点之间的最短路径(有向图)
1、解法


约束条件的理解:i=1表示地点,当然不用回来了,出弧减入弧为1
i=n表示终点,当然不用出去了,出弧减入弧为-1
其他点有出有进,所以为0
2、demo
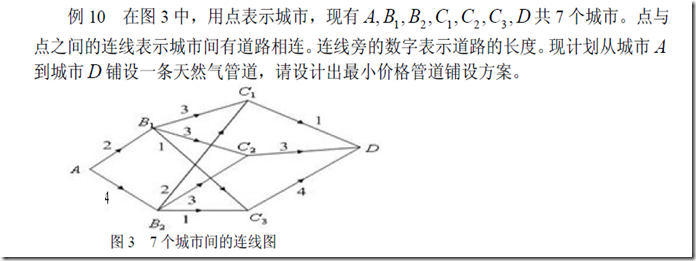
思路一:
以dp的思想来做,这样的话,通过递归来做就可以
思路二:
直接遍历,但是进行一个比较,明显不是最优解的省去
(四)树
一、基本概念
这里讲解的树为连通图的生成树。
二、应用——连线问题
![]()
解题思路:就是在连通赋权图上求解出最小生成树。
算法一:prim算法构造最小生成树
1、思想:
先定义一个顶点的集合,定义一个边的集合。然后构造一个最小生成树。然后选一点,从这点出发,一直寻找权重最小的边,加入到边的集合,直到涵盖了全部顶点为止。
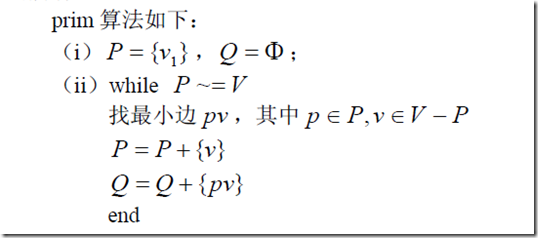
2、demo
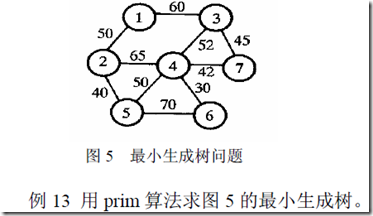
clc;clear; a=zeros(7);a(1,2)=50;a(1,3)=60; a(2,4)=65;a(2,5)=40; a(3,4)=52;a(3,7)=45; a(4,5)=50;a(4,6)=30;a(4,7)=42; a(5,6)=70;a=a+a'; a(find(a==0))=inf; result=[];p=1;tb=2:length(a); while length(result)~=length(a)-1temp=a(p,tb); %取出p向量里储存的顶点到其他未选中的点的边temp=temp(:);d=min(temp); %从中取出最小的,加入到result,将这个边的终点加入向量p[jb,kb]=find(a(p,tb)==d);j=p(jb(1));k=tb(kb(1));result=[result,[j;k;d]];p=[p,k];tb(find(tb==k))=[]; endresult
算法二:Kruskal算法
1、思想
用index来存储各边端点的信息,当选中某一个边的时候,就将这边较的端点改为较小的端点,把后面的出现的也一并改掉,也就是所把这条边删掉。
2、demo
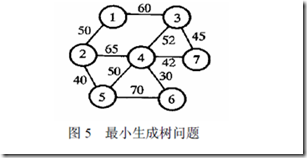
clc;clear;a(1,2)=50;a(1,3)=60; a(2,4)=65;a(2,5)=40; a(3,4)=52;a(3,7)=45; a(4,5)=50;a(4,6)=30;a(4,7)=42; a(5,6)=70;[i,j,b]=find(a); data=[i';j';b']; %data存储每条边的端点和权值,index记录每条边的端点 index=data(1:2,:); loop=max(size(a))-1; result=[];while length(result)<looptemp=min(data(3,:));flag=find(data(3,:)==temp);flag=flag(1);v1=data(1,flag);v2=data(2,flag); %每次找到之后,将数据存入data,而index就开始将线变成点,主要就是用来检验已经取过的树有没有已经走过这两点,
%从而避免圈的出现。if index(1,flag)~=index(2,flag)result=[result,data(:,flag)];endindex(find(index==v2))=v1;data(:,flag)=[];index(:,flag)=[]; endresult
(五)匹配问题
一、一些概念的理解= =


M其实就是边两端的点集
二、人员分配问题
1、提出

2、解决的算法
(1)匈牙利算法

(六)Euler图和Hamilton图
一、基本概念
1、Euler定义
![]()
Euler图就是能够不重复且走过每条边能够回到出发点的图。
2、定理:

3、Hamilton定义

Hamilton图就是能够不重复且走过每个顶点能够回到出发点的图。
二、Euler回路的Fleury算法
