建筑模板915 1830价格/企业seo顾问公司
，不过我想这并不影响学习的心情。上一篇在最后已经说过，从本篇开始，会有一段时间都将用于记录数组、矩阵的操作等等，如果以前没有接触过相关的，可能会觉得要展示的是很复杂的东西，但并不是，这是一个很简单的部分，但也是一个很重要的部分，至少现在的我觉得这部分的内容可以说是MATLAB精髓之一吧，毕竟该系统的运算是基于矩阵进行的，在MATLAB系列最开始的篇章中就已经有说过一些，当然，你们也可以保持自己的意见，毕竟这只是我觉得，你们觉得该咋样还是咋样，但是不管怎么说，接下来的篇章中关于矩阵的这部分内容很重要就对了
~Show Time~
要了解一个东西，就应该知道它是如何产生的，这些在之前的文章中都有过接触，所以这边就再简单说下它生成的方法。
1、直接生成
直接使用方括号“[ ]”实现，在方括号内输入元素，不同行用分号分隔开，不同列可以使用空格，也可以使用逗号。
例：A=[1 2 3; 4 5 6]
除了上面这种最直接的生成，还有一个比较快捷的生成，不过这些数需要是有一定的排列规则，使用的是一个“:”。
比如：A=[1:3;4:6]
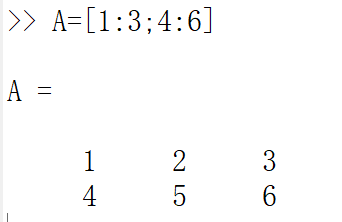
冒号在MATLAB中是一个很重要的运算符，因为可以用它产生行向量，一般表达式我想你也猜出来大概了；
语法：e1:e2:e3
e1是初始值，e2是步长，e3是终止值，因此冒号表达式产生的就是一个从e1开始到e3结束，以步进e2逐渐累加的行向量，像刚刚的例子中没有写步长的就是默认步长为1，如果要指定步长的形式，则是t=1:1:3这样所示。再补充一个，除了冒号表达式可以产生行向量之外，还能使用linspace函数产生，调用格式：linspace(a,b,n)a和b分别代表将要生成的行向量的第一个和最后一个元素，n是总元素个数，如果省略n，则系统会默认产生100个元素，然后其增加行向量值的计算方法和冒号的方式差不多，都是累加的形式，linspace(a,b,n)和a:(b-a)/(n-1):b是等价的，就不做演示了，可以自己实践操作学习下，接着讲下一种生成矩阵的方法。
2、函数生成
使用一些特殊函数生成特殊的矩阵，在之前的文章中也已经有过记录，不过为了更加系统化，就再进行介绍一下，先演示两个：A=zeros(3,2)%产生3行2列的零矩阵
A=eye(3)%产生3*3的单位矩阵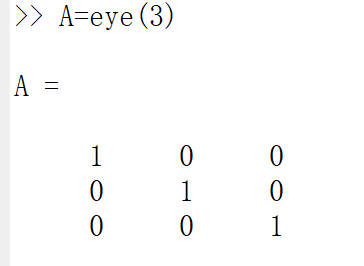
矩阵 | 函数 |
全零矩阵 | zeros |
单位矩阵 | eye |
全1矩阵 | ones |
均匀分布随机矩阵 | rand |
正态分布随机矩阵 | randn |
产生线性等分向量 | linspace |
产生对数等分向量 | logspace |
Wilkinson特征值测试矩阵 | wilkinson |
友矩阵 | compan |
Hadamard矩阵 | hadamard |
Hankel矩阵 | hankel |
Hilbert矩阵 | hilb |
逆Hilbert矩阵 | invhilb |
Magic矩阵 | magic |
Pascal矩阵 | pascal |
托普利兹矩阵 | toeplitz |
阅读本文共使用 
秒
电子知识
一些电路设计与DIY作品
电子设计技巧与经验
FPGA
System Generator系列教程
算法介绍
通信协议分析
资料分享
Matlab系列记录
建设中~
点个赞
再走吧