2021年03月18日 周四 天气晴 【不悲叹过去，不荒废现在，不惧怕未来】

---

1. 问题简介

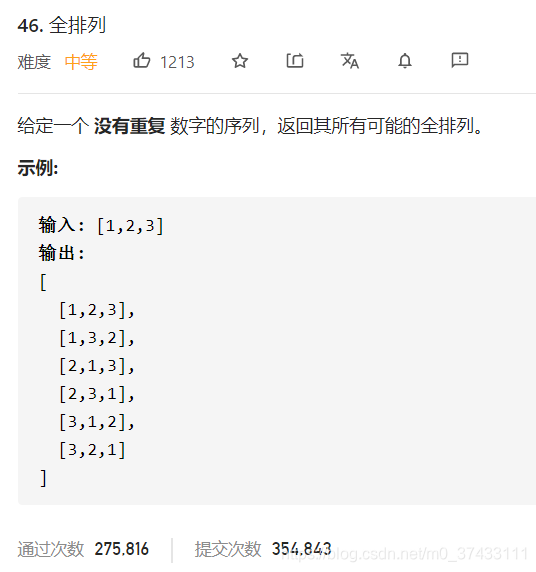
46. 全排列

2. 题解（回溯大法）

2.1 临时数组法

class Solution {
public:unordered_set<int> uset; // 利用哈希表判断元素是否遍历过了vector<vector<int>> res;vector<vector<int>> permute(vector<int>& nums) {vector<int> tmp; // 临时数组，存放每一个排列的结果dfs(nums,tmp,0);return res;}void dfs(vector<int>& nums, vector<int>& tmp, int n){// 终止条件，所有位都遍历完了if(n==nums.size()){res.push_back(tmp);return;}for(int num:nums){// 如果 num 还没有遍历if(uset.find(num)==uset.end()){// 加入哈希表和临时数组uset.insert(num);tmp.push_back(num);// 继续遍历下一位dfs(nums,tmp,n+1);// 遍历完之后记得还原，避免分支污染uset.erase(num);tmp.pop_back();}}}
};

这是我第一次做的时候写出的答案，比较容易理解。虽然可以通过，但是要比官方法（下面的交换法）更加耗时一些。

2.2 交换法

class Solution {
public:void backtrack(vector<vector<int>>& res, vector<int>& output, int first, int len){// 所有数都填完了if (first == len) {res.emplace_back(output);return;}for (int i = first; i < len; ++i) {// 动态维护数组swap(output[i], output[first]);// 继续递归填下一个数backtrack(res, output, first + 1, len);// 撤销操作swap(output[i], output[first]);}}vector<vector<int>> permute(vector<int>& nums) {vector<vector<int> > res;backtrack(res, nums, 0, (int)nums.size());return res;}
};

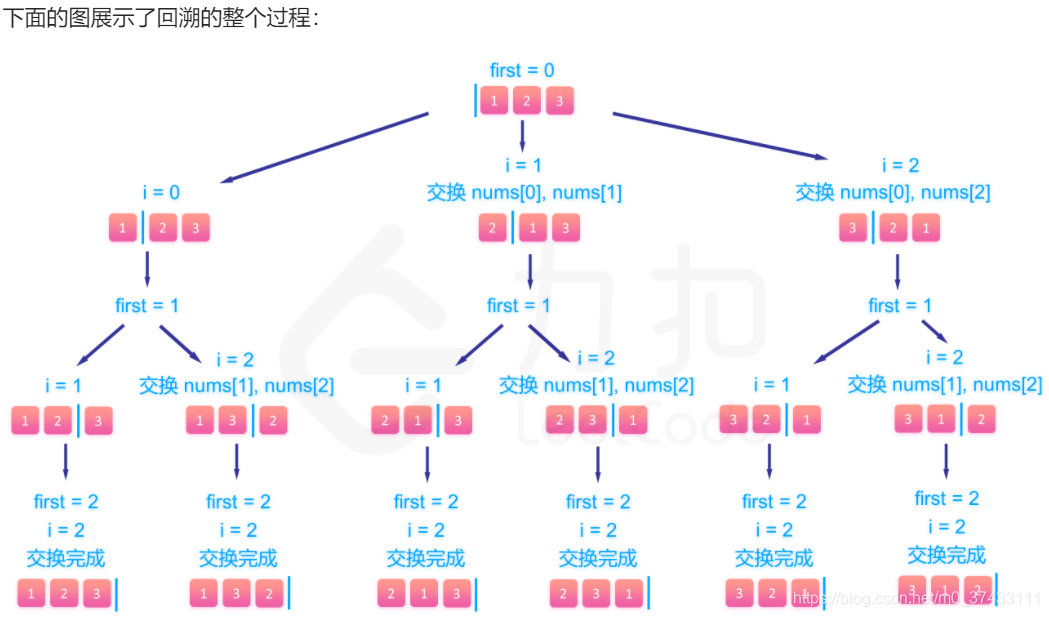
交换法也是解决全排列问题的标准方法了，代码虽然简单，但是理解起来会稍微费点劲儿。

下面这张图帮助理解：

*复杂度分析

时间复杂度的计算比较难懂，可以参考下面这张图进行理解：

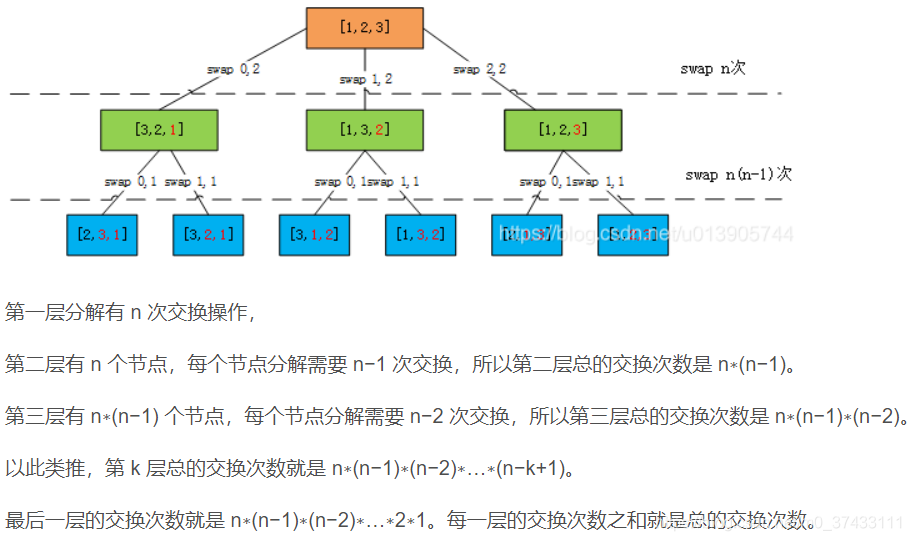
把每一层的交换次数加起来，可以得到总的调用次数为：

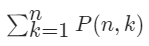
然后就能进行上面的公式推导了。

---

参考文献

https://leetcode-cn.com/problems/permutations/solution/quan-pai-lie-by-leetcode-solution-2/

https://blog.csdn.net/u013905744/article/details/113779407