题目大意:
给你一个有向图,问每个点能够到达的点中编号最大的点。
思路:
假如这个图是一个树的话就这个题目就很好做了,首先我们设\(A[i]\)为每个点能够到达的编号最大的点。因为当前结点的儿子能够到达的点中的编号最大的点当前结点一定可以到达。然后当前结点中所以这里很明显\(A[i]\)的值可以有它子结点的值转移而来,所以我们得到了一个转移方程:
\[ A_i = max(A[v],i)\]
其中\(v\)为\(i\)的子结点。
但是很遗憾我们题目中的图并不是一个树,而是一个有向图,所以\(A_i\)可以从更早遍历到的点\(x\)的\(A[x]\)转移而来。如下图:
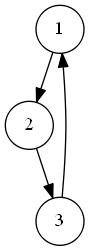
要解决上面这个问题,我们可以用Tarjan算法缩点把图变为一个有向无环图。或者采用多次遍历的方法来解决。但这两个方法不是太难写要么就是会T(使劲卡常可以把这个题目卡出90分)。然后我们来讲讲一个简单好写又快的方法:
首先我们先反向建边,也就是假如我们本来要建一个从3到1的边,现在我们建一个从1到3边。然后从每个结点开始遍历假如遍历到的点的\(A\)的值没有起点的编号大,那么就更新这个点的\(A\)值。
代码:
#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>using namespace std;const int N = 1e5 + 5;int n, m;
int u, v;
int a[N];
int cnt = 0;
int head[N];
bool vis[N];
bool check[N];struct EDGE {int s;int e;int nxt;
} Edge[N];void add(int u, int v) {++cnt;Edge[cnt].s = u;Edge[cnt].e = v;Edge[cnt].nxt = head[u];head[u] = cnt;
}int Min(int x, int y) {return x <= y ? x : y;
}int Max(int x, int y) {return x >= y ? x : y;
}void dfs(int x, int ans) {vis[x] = true;a[x] = Max(a[x], ans);for (register int i = head[x]; i; i = Edge[i].nxt) {if (vis[Edge[i].e]) continue;dfs(Edge[i].e, ans);}
}int main(int argc, char const *argv[]) {scanf("%d %d", &n, &m);for (register int i = 1; i <= m; ++i) {scanf("%d %d", &u, &v);add(v, u);}for (register int i = n; i >= 1; --i) dfs(i, i);for (register int i = 1; i <= n; ++i) printf("%d ", a[i]);putchar('\n');return 0;
}
