网站设计技术有哪些/深圳网络营销平台
1.Probit回归分析简介Probit回归的典型应用是杀虫剂浓度和杀死害虫数量之间的关系，并据此判断什么样的剂量浓度时最佳的。在药学研究中，此方法常用于半数效应分析(Median effect dose)，寻求达到50%输出响应的输入刺激量。1.1数学原理同logistic回归分析中的Logit变换类似，由于线性模型的某些限制，Probit回归需要把取值分布在实数范围内的变量通过累计概率函数f转换成取值分布在(0，1)区间的概率值。1.2.数据要求- 响应变量应该是计数信息，记录在指定的自变量条件下，有响应的观测个数。
- 因变量必须是分类变量，且须用整数编码。
- 观测量应该是独立的，否则卡方检验和拟合优度检验是不适宜的。
- 半数效应。举个例子，如收入到多少时，有一般家庭会购买。毒素浓度达到多少时，有一半的小鼠会死亡。
- Probit回归更适用于从有计划的试验中获得的数据，而Logistic回归更适用于直接观测数据。
- Probit回归输出对各种响应比例有效值的估计，而Logistic回归输出对自变量的发生比(odd)的估计。
2.案例分析某零售公司在不同的营业场所(网上、货架和店铺)采用了不同的促销价格，请使用Probit回归对不同促销价格和对促销有反馈的顾客数量之间的关系进行分析，并拟合相应模型。2.1. 数据描述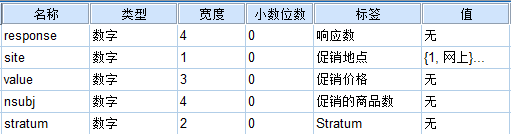
response：顾客响应数；(离散)site：促销地点(网上促销=1，货架促销=2，店铺促销=3)；(离散)value：促销价格；(离散)nsubj：促销的商品数；(离散)2.2 概率单位回归的参数设置Step1：变量及模型设置。分析->回归->概率，如图将相应的变量选入选项框内，一般我们选择转换函数为自然对数。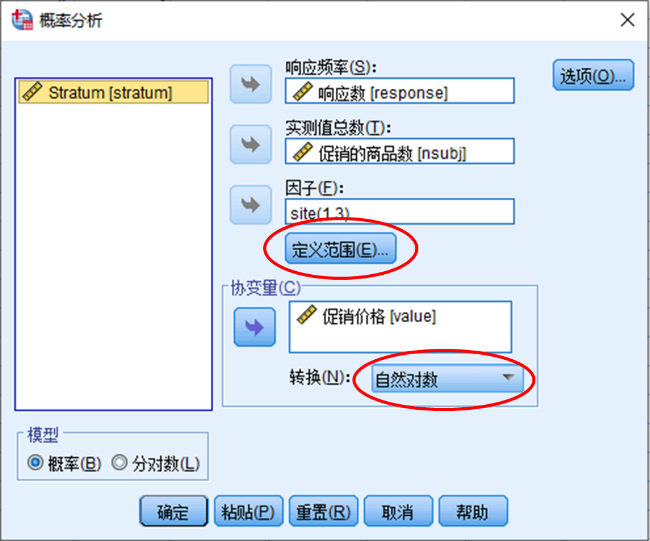
Step2：选项设置。进入选项框：勾选平行性检验、点选根据数据计算、最大迭代次数输入100次，如图所示。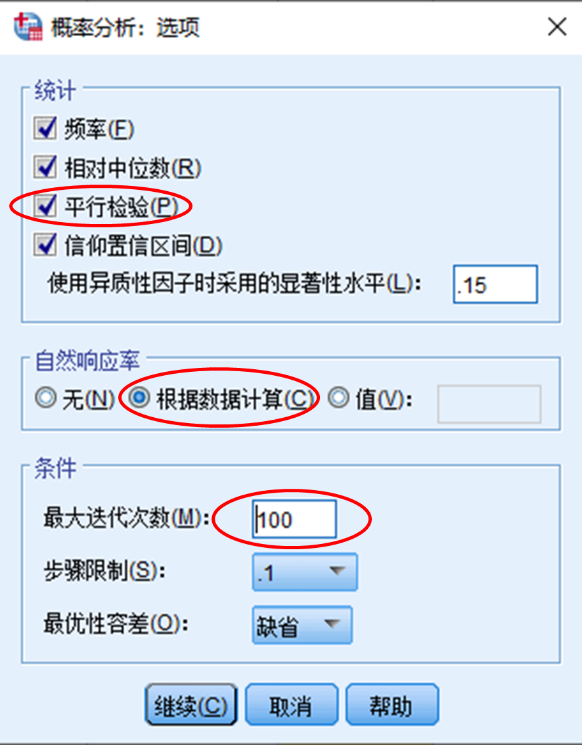
平行性检验：零假设是因变量各分组的回归方程具有相同的斜率。
自然响应率：指在没有刺激条件下(本例中是指没有促销活动的条件下)，是否有自然的响应率(是否仍然有顾客购买产品)。
参数设置并不复杂，关键是我们要分清楚各个变量的属性，哪些变量是响应频率，哪些变量是实测总数，因子和协变量分别是哪些。本例中，我们研究的是不同促销价格对反馈顾客数量比例之间的关系，因此反馈的顾客数量(response)作为因变量，为响应频率；不同促销价格(value)是因变量，为协变量；促销前的商品数(nsubj)为实测值总数；促销地点有三种，我们要考察三种不同促销地点的促销价格与顾客响应数的关系，因此促销地点(site)为因子(即分组)变量。
3.结果分析设置好参数后，点击继续和确定得到输出结果如图所示。
(1)参数估计值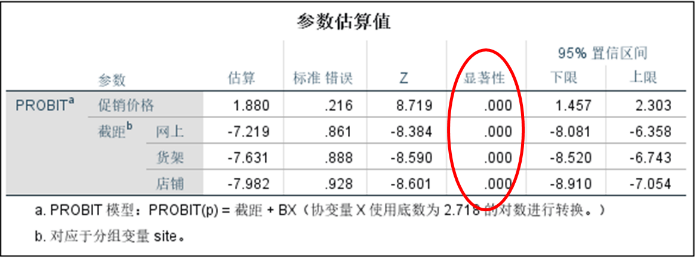
所有参数的显著性检验Sig值都远小于0.01，说明协变量和三个截距项对方程的作用都有显著意义。由此可得，对3种营业场所的Probit回归方程如下：
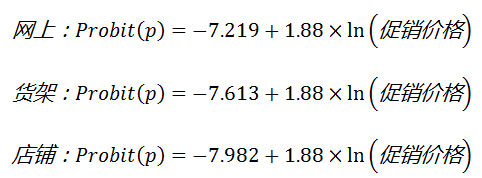
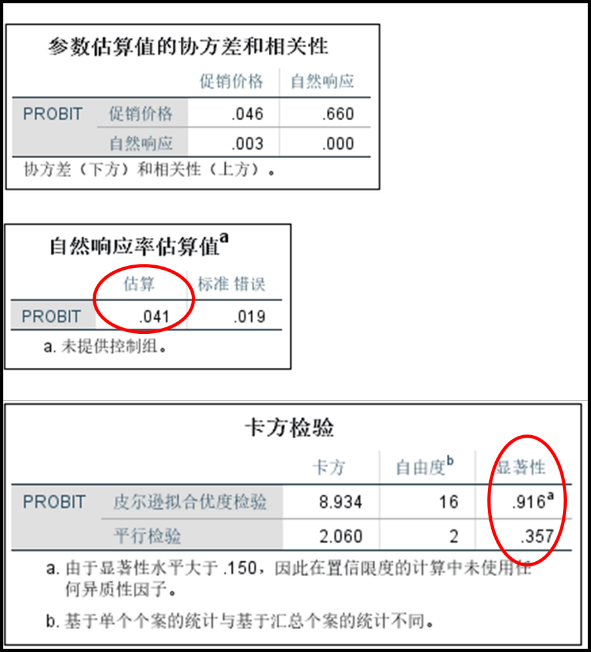
“自然响应率估算值”表格给出了对自然响应率的估计值，可见在没有促销活动的情况下，总顾客中仍会有4.1%的人购买产品；
“卡方检验”表格中，Person拟合优度卡方检验的零假设为模型能够很好的拟合数据，显著性Sig值远大于0.1，不能拒绝原假设，即模型对数据的拟合较好。平行检验的显著性值Sig也远大于0.1，所以认为因变量各分组的回归方程具有相同的斜率。
(3)置信区间表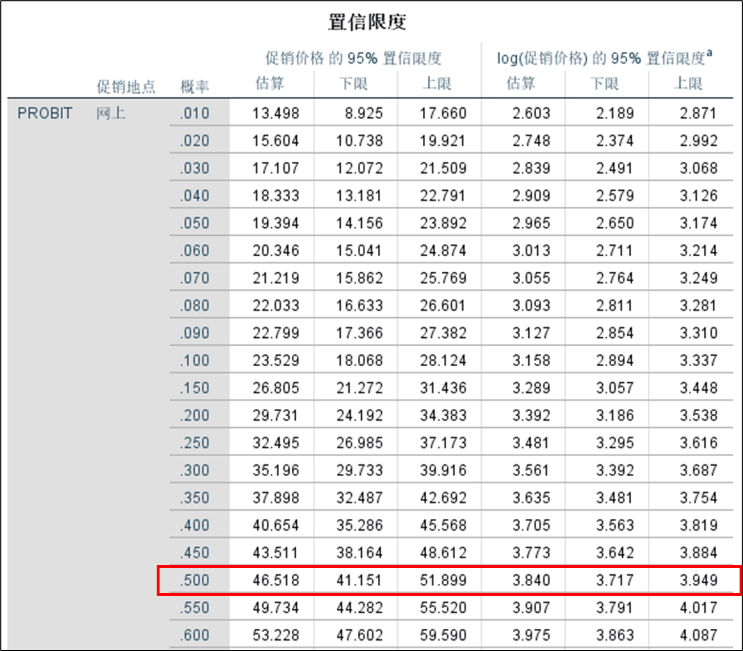
该表显示的是制定销售地点的相应概率，在达到各百分位电视的促销价格估计值及其95%的置信区间，图中只截取了关于网上促销的部分结果，其余还有货架、店铺等两个类别的估计结果。可见，相应概率Probit =0.500时，网上促销价格的半数响应估计值为46.518；同理可知，货架促销和店铺促销的价格半数半数响应估计值分别为57.905和69.800。由此可以得到如下结论：网上促销比货架促销更有效，货架促销比店铺促销更有效。
(4)相对中位数强度估计值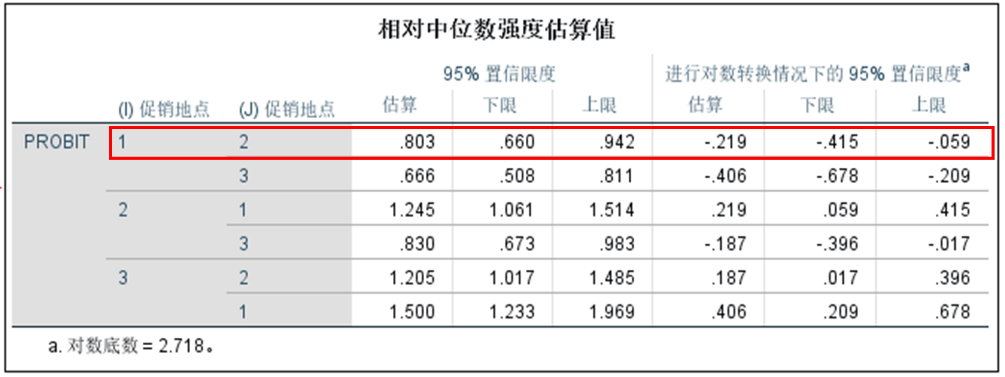
以第一行为例来说明如何分析此表。第一行显示的是网上促销(地点取值为1)对货架促销(地点取值为2)的相对半数效应，网上与货架半数效应比值的估计值为0.803，且其95%的置信区间为[0.660，0.942]不包括1，说明二者是有明细区别的，也就是说网上促销更有效，因为它能以较小的促销价格促使50%的客户购买产品(即达到50%的响应率)。通过此表也可以发现，网上促销比货架促销更有效，货架促销比店铺促销更有效。
(5)散点图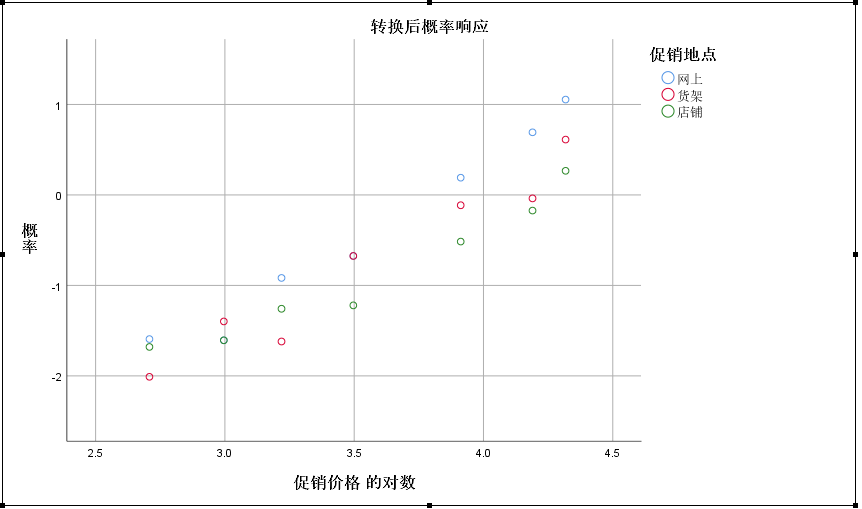
响应概率与对数促销价格呈明显的线性关系，说明对促销价格所作的自然对数转换是比较合适的，如果散点图没有呈现明显的线性趋势，可以再采用其他转换方法进行分析。另外，网上促销的Probit值普遍大于货架促销，货架促销的Probit值普遍大于店铺促销，这也反应了网上促销比货架促销更有效，货架促销比店铺促销更有效。