本地搭建linux服务器做网站/优化师培训
大三时候在跳蚤市场闲逛,从一位数学院的学长那里买了一些闲书,最近翻出来刚好有李荣华、刘播老师的《微分方程数值解法》和王仁宏老师的《数值逼近》,结合周善贵老师的《计算物理》课程,整理一下笔记。
本文整理常微分方程数值求解的欧拉法与龙格-库塔法。
一般地,动力学系统的时间演化可以用常微分方程的初值问题来描述,例如设一维简谐运动的回复力:
因此本文主要整理一阶常微分方程初值问题的数值解法。
一阶常微分方程初值问题
设
存在常数L,使得
假设
欧拉法
将区间
推导
1、根据泰勒展开式:
略去二阶小量,得:
以此类推,得到递推公式:
2、数值积分推导
由
以此类推,可得到:
为了提高精度,可以使用梯形积分代替矩形积分,即:
以此类推,得到改进的欧拉法:
Python计算实例
以
import math
from matplotlib import pyplot as pltt_0 = 0
y_0 = 1
tau = 0.1
i = 1
solve = []
Euler = []
t = []
while i < 100:if i == 1:y_n = y_0t_n = t_0Euler.append(y_n)solve.append(math.exp(t_n))t.append(t_n)func = y_ny_n = y_n + tau * funct_n = t_n + taui += 1plt.plot(t, Euler, c='green', label=' Euler method')
plt.plot(t, solve, c='red', label=' accuracy')
plt.fill_between(t, solve, Euler, facecolor='blue', alpha=0.2)
plt.title('Euler method', fontsize=19)
plt.xlabel('t', fontsize=19)
plt.ylabel('y', fontsize=19)
plt.legend()
plt.show()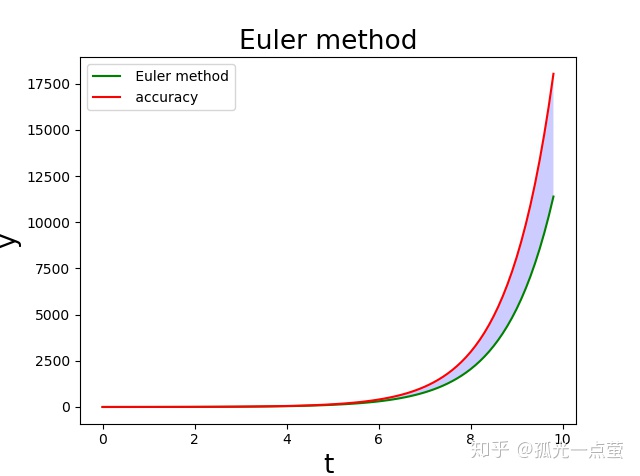
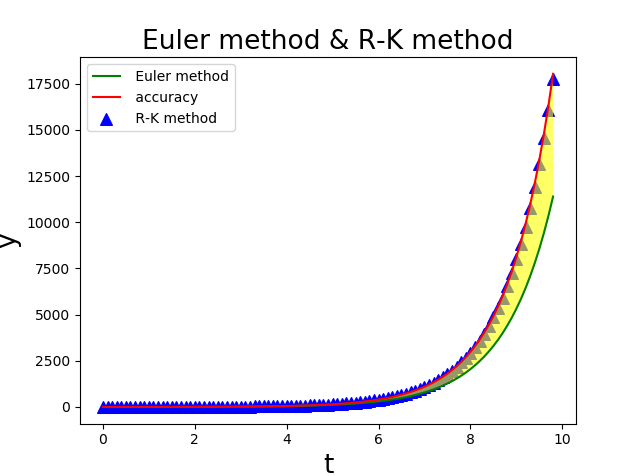
作图可以看到,当迭代步数较多后,欧拉法的结果逐渐落后于精确指数解的增长速度。下面分析欧拉法的误差来源。
在
在计算中,我们更关心精确解和数值解之间的误差
根据Lipschitz条件,可得:
由
局部截断误差
稳定性分析
如果计算的初值不能精确给定,例如存在测量、舍入误差等,在计算过程中,每一步传递的误差连续依赖于初始误差,则称算法稳定,否则该算法不稳定。
对于不同的初值
两式相减,得:
根据Lipschitz条件,可得:
龙格-库塔法
龙格库塔法的主要思想:在
将
令
以此类推,可以得到:
同时,我们可以写出泰勒展开的形式解:
其中:
通项为:
基本思路是,利用当前点的函数值
现在把
将
将
与泰勒展开式
2个方程有3个未知数,因此有无穷多个解,可采用
令
此即为二阶龙格-库塔法。
与上一节的欧拉法公式对比:
Python计算实例
仍以
import math
from matplotlib import pyplot as pltt_0 = 0
y_0 = 1
z_0 = 1
tau = 0.1
i = 1
j = 1
solve = []
Euler = []
R_K = []
t = []
while i < 100:if i == 1:y_n = y_0t_n = t_0R_K.append(y_n)solve.append(math.exp(t_n))t.append(t_n)func_n = y_nfunc_m = y_n + tau * func_ny_n = y_n + 0.5 * tau * (func_n + func_m)t_n = t_n + taui += 1
t = []
while j < 100:if j == 1:z_n = z_0t_n = t_0Euler.append(z_n)t.append(t_n)func = z_nz_n = z_n + tau * funct_n = t_n + tauj += 1plt.scatter(t, R_K, marker='^', c='blue', s=70, label=' R-K method')
plt.plot(t, Euler, c='green', label=' Euler method')
plt.plot(t, solve, c='red', label=' accuracy')
plt.fill_between(t, solve, Euler, facecolor='yellow', alpha=0.2)
plt.title('Euler method & R-K method', fontsize=19)
plt.xlabel('t', fontsize=19)
plt.ylabel('y', fontsize=19)
plt.legend()
plt.show()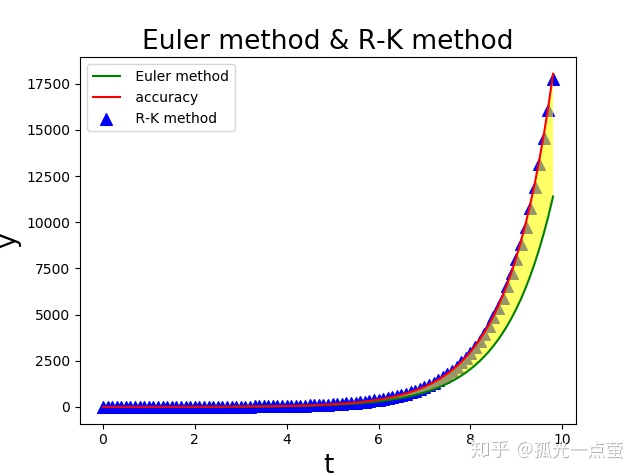
黄色部分表示数值解和精确解的偏离,可以看到,二阶龙格-库塔法(改进的欧拉法)精确度得到了很大的提升。
二阶龙格-库塔法中,泰勒展开到了
Reference:
1、周善贵,《计算物理》课程讲义
2、李荣华,刘播,《微分方程数值解法》
3、王仁宏,《数值逼近》
