单层神经网络
在神经网络中,当隐藏节点具有线性激活函数时,隐含层将无效化。监督学习的训练,正是一个修正模型以减少模型输出与标准输出之间的误差的过程。神经网络以权重形式存储信息。
根据给定信息修改权重的系统方法被称为学习规则。
1.delta规则
也被称为Adaline规则或者Widrow-Hoff规则,是一种梯度下降的数值方法。

这一规则的基本思想是,权重依据输出节点误差和输入节点值成比例地调整。

2.更新权重的策略
SGD(Stochastic Gradient Descent 随机梯度下降):依据每个训练数据计算误差,并立即调整权重。

Batch:使用训练数据的所有误差计算各个权重更新值,然后使用权重更新的平均值调整权重。

Mini Batch:SGD方法和Batch方法的混合。它选择训练数据集的一部分,并将它们用于Batch方法训练,即用平均权重更新来训练网络。若数据点的数量选择得当,Mini Batch可以兼顾SGD的速度和Batch方法的稳定性。
3.delta规则的SGD方法实现(MATLAB)
示例如下图所示,激活函数为Sigmoid函数,训练数据集为{([0,0,1],0),([0,1,1],0),([1,0,1],1),([1,1,1],1)}。
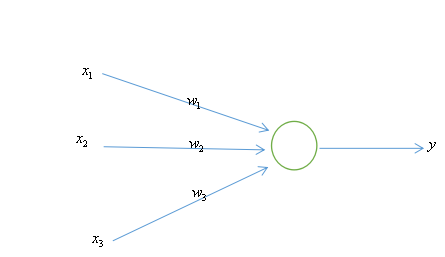
先定义Sigmoid函数:
function y = Sigmoid(x)y = 1 / (1 + exp(-x));
end 定义SGD方法:
function W = DeltaSGD(W, X, D)
% 以神经网络的权重和训练数据作为输入,返回训练后的权重
% W是传递权重的参数,X和D分别为传递训练数据的输入和标准输出的参数alpha = 0.9;N = 4; for k = 1:Nx = X(k, :)';d = D(k);v = W*x;y = Sigmoid(v);e = d - y; delta = y*(1-y)*e;dW = alpha*delta*x; % delta rule W(1) = W(1) + dW(1); W(2) = W(2) + dW(2);W(3) = W(3) + dW(3); end
end
测试一下效果:
clear allX = [ 0 0 1;0 1 1;1 0 1;1 1 1;];D = [ 0011];W = 2*rand(1, 3) - 1;for epoch = 1:10000 % trainW = DeltaSGD(W, X, D);
endN = 4; % inference
for k = 1:Nx = X(k, :)';v = W*x;y = Sigmoid(v)
end
得到结果为 0.0102 ,0.0083 ,0.9932 ,0.9917 。
4.delta规则的Batch实现(MATLAB)
定义Batch函数:
function W = DeltaBatch(W, X, D)alpha = 0.9;dWsum = zeros(3, 1);N = 4; for k = 1:Nx = X(k, :)';d = D(k);v = W*x;y = Sigmoid(v);e = d - y; delta = y*(1-y)*e;dW = alpha*delta*x;dWsum = dWsum + dW;enddWavg = dWsum / N;W(1) = W(1) + dWavg(1);W(2) = W(2) + dWavg(2);W(3) = W(3) + dWavg(3);
end
Batch方法的平均性特性使得训练数据的敏感性降低。速度比SGD慢。
测试该函数:
clear allX = [ 0 0 1;0 1 1;1 0 1;1 1 1;];D = [ 0011];W = 2*rand(1, 3) - 1;for epoch = 1:40000 W = DeltaBatch(W, X, D);
endN = 4;
for k = 1:Nx = X(k, :)';v = W*x;y = Sigmoid(v)
end
输出的结果为 0.0102,0.0083,0.9932,0.9917。
5.SGD和Batch的比较
比较两种方法的平均误差。将训练数据输入到神经网络中,并计算出均方差(E1,E2)
clear allX = [ 0 0 1;0 1 1;1 0 1;1 1 1;];D = [ 0011];E1 = zeros(1000, 1);
E2 = zeros(1000, 1);W1 = 2*rand(1, 3) - 1;
W2 = W1;for epoch = 1:1000 % trainW1 = DeltaSGD(W1, X, D);W2 = DeltaBatch(W2, X, D);es1 = 0;es2 = 0;N = 4;for k = 1:Nx = X(k, :)';d = D(k);v1 = W1*x;y1 = Sigmoid(v1);es1 = es1 + (d - y1)^2;v2 = W2*x;y2 = Sigmoid(v2);es2 = es2 + (d - y2)^2;endE1(epoch) = es1 / N;E2(epoch) = es2 / N;
endplot(E1, 'r')
hold on
plot(E2, 'b:')
xlabel('Epoch')
ylabel('Average of Training error')
legend('SGD', 'Batch')
结果如下:
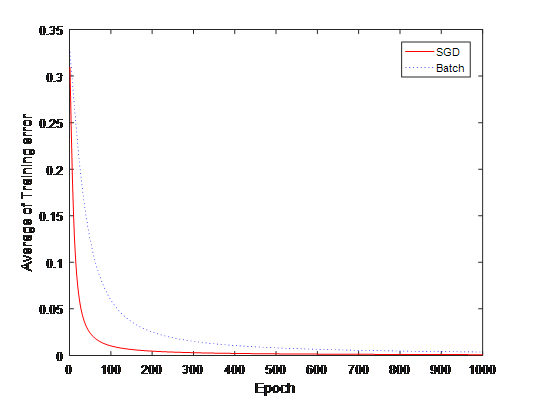
6.单层神经网络的局限性
我们知道,单层神经网络无法拟合异或。下面测试一下,输入改成异或数据,DeltaXOR与DeltaSGD代码一样。
clear allX = [ 0 0 1;0 1 1;1 0 1;1 1 1;];D = [ 0110];W = 2*rand(1, 3) - 1;for epoch = 1:40000 % trainW = DeltaXOR(W, X, D);
endN = 4; % inference
for k = 1:Nx = X(k, :)';v = W*x;y = Sigmoid(v)
end
结果为 0.5297,0.5000,0.4703,0.4409。这个结果明显存在问题。
单层神经网络只能解决线性可分问题,这是因为单层神经网络是一种将输入数据空间线性划分的模型。为克服单层神经网络的这种局限,出现了多层神经网络。
