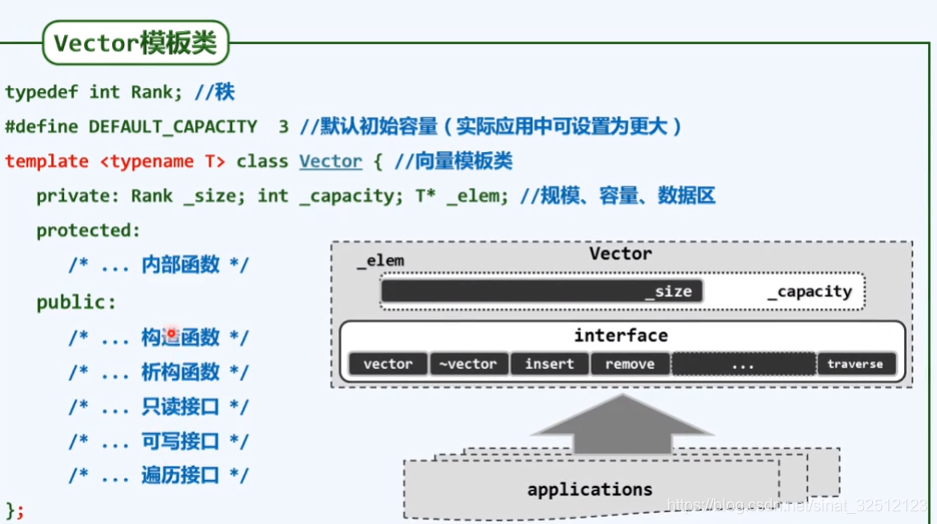
接口与实现

接口与实现

抽象数据类型(ADT,Abstract Data Type )与数据结构(Data Structure)


ADT相当于一种说明书

int n;
float x;
char c;
Vector myVector;
List  myList;

向量ADT

从数组到向量

向量ADT接口

接口操作实例

disordered存在多少个紧邻的逆序对是降序的；
当找不到想要找的那个元素时，返回-1，或则返回不超过所要找的那个元素的最大元素的秩；如果重复，则是最后面对应的秩。
用sort对整个向量排序，排成升序。

构造与析构

最后一个是解析：

复制

基于复制的构造
1.首先开辟出足够容量的空间
2.再将区间内的元素逐一复制过来

可扩充向量

静态空间管理

动态空间管理

扩容算法实现

增递式扩容

假如容量每次只加I，则为容量递增策略

加倍式扩容

容量加倍策略

分摊复杂度

无序向量

概述

Template<typename T>             //Vector{……}
Vector<int 或float或char……>     //myVector
Vector<BinTree>//forest;

循秩访问

元素访问
C++中的左值和右值

插入

右移

区间删除

为什么_size=lo?

单元素删除

查找

最终hi可能是查找的那个位置，也有可能是失败的位置。而当hi<lo时，则意味着失败。

唯一话：算法

证明它的正确性？

复杂度

遍历

后者的适用性更强
实例：

有序向量：唯一化

有序性

无序：比对（是否相等）
有序：比较（孰大孰小）

有序性及其甄别

唯一化（低效版）

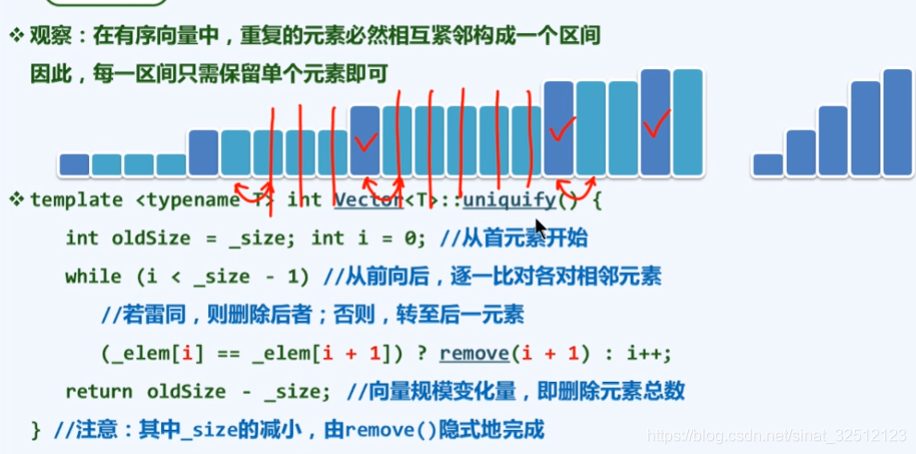
复杂度（低效版）

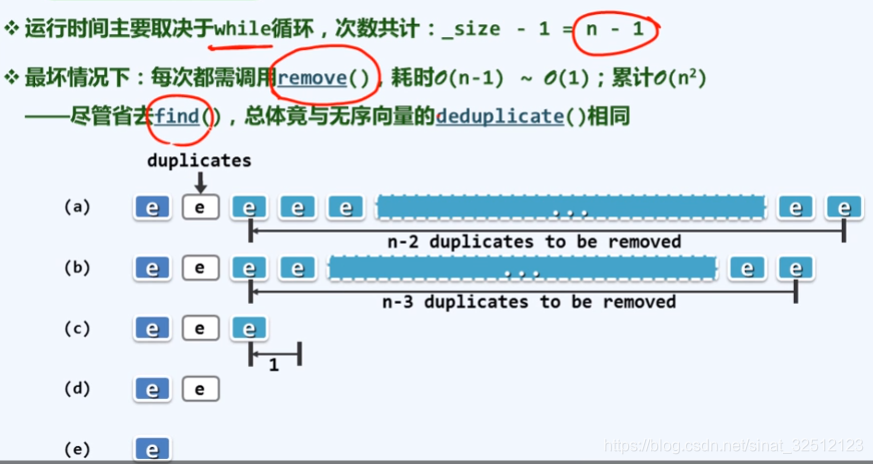
唯一话（高效版）

成批地删除？
从最下方的图来看，duplicates表示与i相同的元素。直接从j跳到i的后一位。
else的话开始下一个while.

实例与分析（高效版）

高效算法：实例与复杂度
共计n-1次迭代，每次常数时间，累计O(n)时间

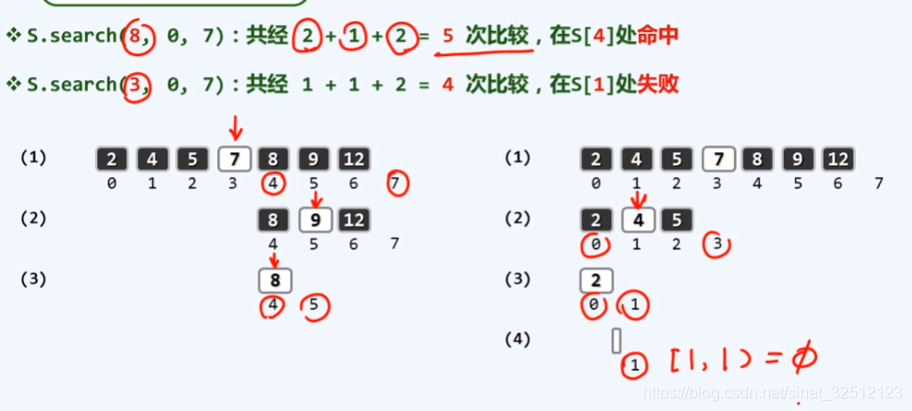
有序向量：二分查找

概述

之前的无序查找：

Vector::find(e,lo,hi)

有序查找中：

Vector::search(e,lo,hi)

接口

从语义上来理解

语义

1+V.search(e)表示e查到的位置再加1，
这样即使失败，我们也需要给出新元素插入的适当的位置。给后继者提供一个参考的依据。
如果查找的值有多个，则返回最后一个再加一的地方插入新的值。还有两种情况，见下图的最后两行。

原理

版本A：

实现

版本A：

建议用小于号

实例

顺序查找的话 复杂度是O(n)

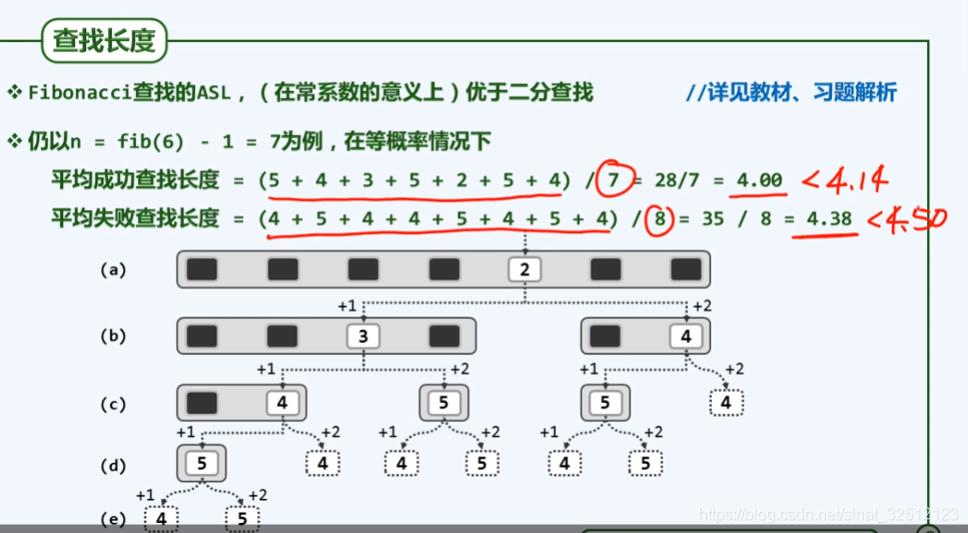
查找长度

版本A：

（a）（b）（c）是成功的情况，一共七种，平均=总次数/7种=29/7=4+
（d）是失败的情况，一共八种，平均=总次数/8种=36/8=4.5=$1.5{\log }_{2}8$

有序向量：Fibonacci查找

构思

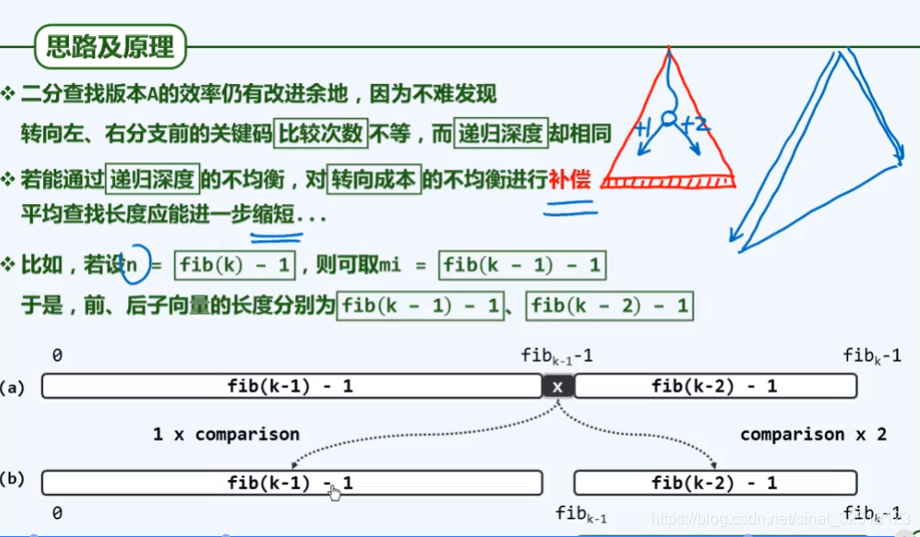
实现

实例

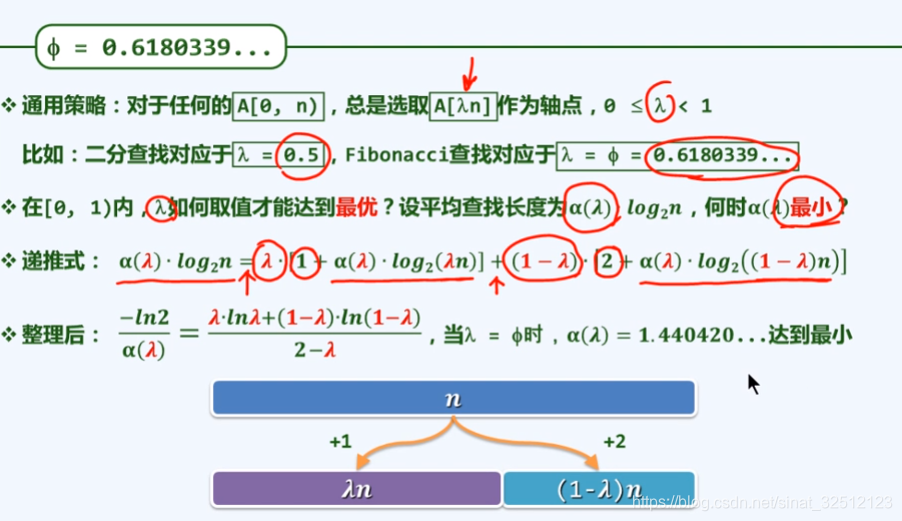
最优性

有序向量：二分查找（改进）

版本B

实现

语义

版本B

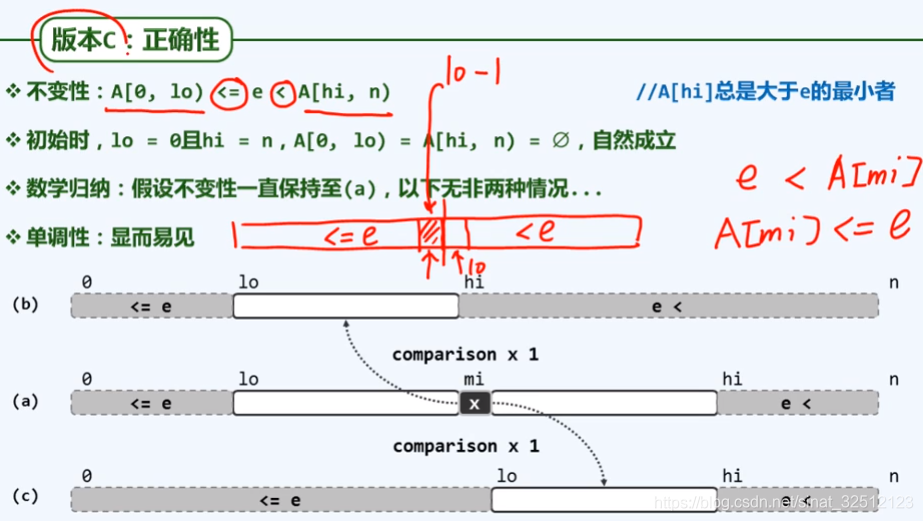
版本C

版本C的正确性

有序向量：插值查找

Interpolation Search

原理

## 实例

性能
最坏情况：O(hi-lo)=O(n),这和平凡的顺序查找没啥区别。
一般情况：平均而言的查找成本=？
最好情况：稍试即中、初试即中。

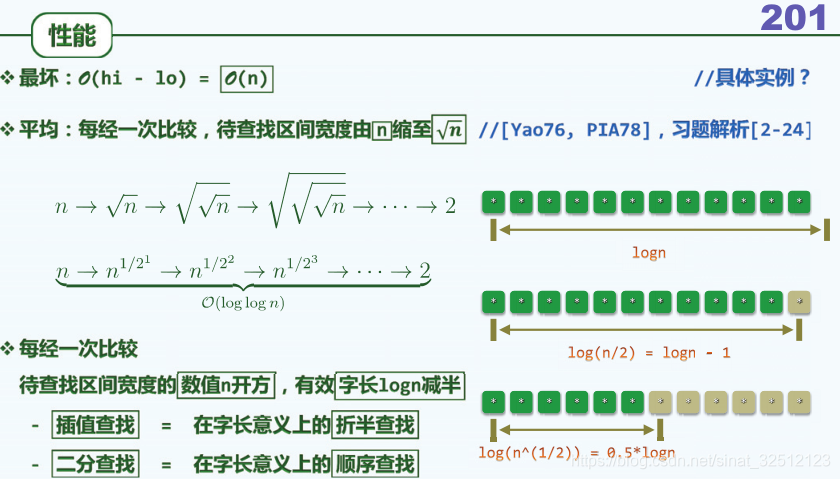
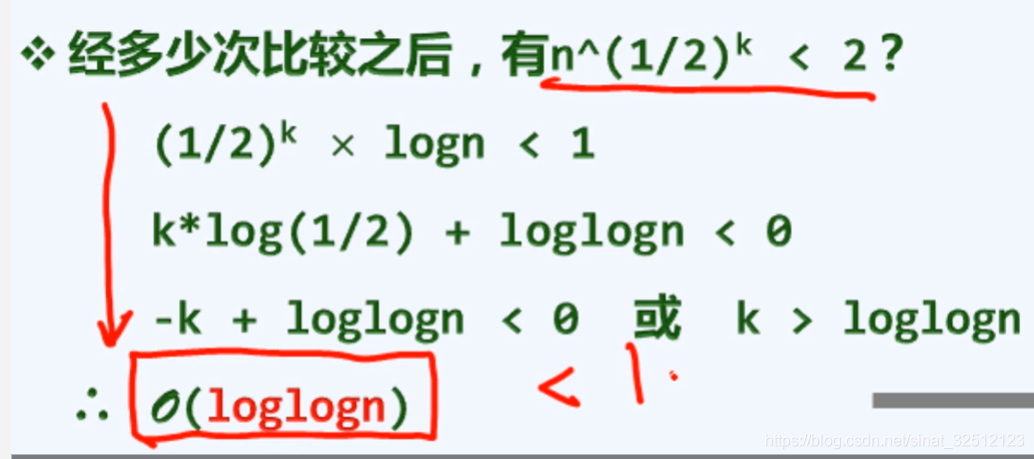
字宽折半

二进制位宽度

综合对比

大规模：插值查找
中规模：折半查找
小规模：顺序查找