自建网站 支付宝/郑州疫情最新动态



1.算法效率的度量方法

1.算法效率的度量方法

效率高一般指：算法的执行时间快。

事后统计方法

这种方法主要是通过设计好的测试程序和数据，利用计算机计时器对不同算法编制程序的运行时间进行比较，从而确定算法效率的高低。

但这种方法显然是有很大的缺陷的，不同测试环境差别不是一般的大！

事前分析估算方法

在计算机程序编写前，依据统计方法对算法进行估算。

2.高级语言编写的程序在计算机上运行耗时取决于下列因素：

－1.算法采用的策略，方案

－2.编译产生的代码质量

－3.问题的输入规模

－4.机器执行指令的速度 由此可见，抛开这些与计算机硬件、软件有关的因素，一个程序的运行时间依赖与算法的好坏和问题的输入规模。(所谓的问题输入规模是指输入量的多少)

3.函数渐进增长: 案例分析

1: 我们分析一下高斯先生的算法

算法1:



算法2:



算法1 执行 1+(n+1)+n=2n+2 次。

算法2 执行 1+1=2 次。

如果忽略头尾的开销，只把循环看过一个整体，2个算法的差距就是： n和1的区别。

2: 分析忽略的原因 n2 的故事



案例中，循环条件 i从1到100，每次让j循环100次，如果非常较真的研究总共精确执行次数，那是非常累的。

我们研究算法的复杂度，侧重的是研究算法随着输入规模扩大增长量的一个抽象，而不是精确的定位需要执行多少次。 因为如何这样的话，我们就又得考虑回编译器优化等问题，然后，就都是然后叻。。!

所以，对于刚才例子的算法，我们可以果断判定需要执行1002次。

看下图， n2 在数据量不断增加的过程中，增长趋势是什么样的



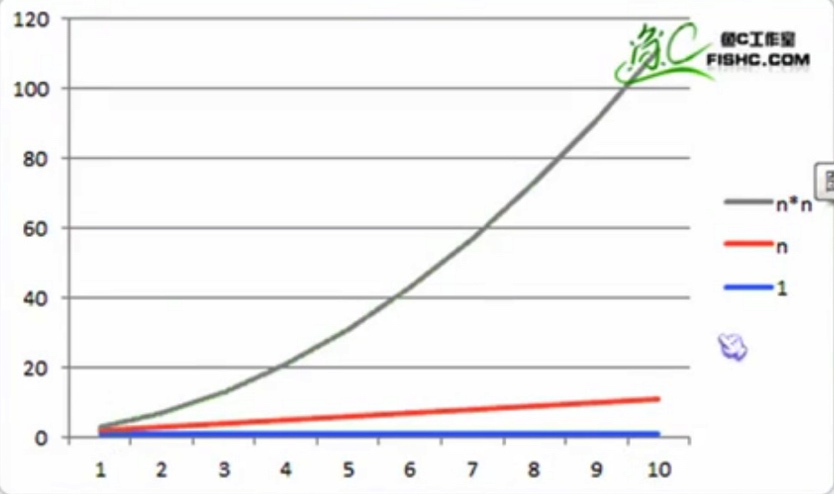
3: 分析忽略的原因 n 的故事

我们来测试一下算法A和B哪个更好？

A1: y=2n+3 A2: y=2n

B1: y=3n+1 B2: y=3n

我们来看图来分析：黑马反超





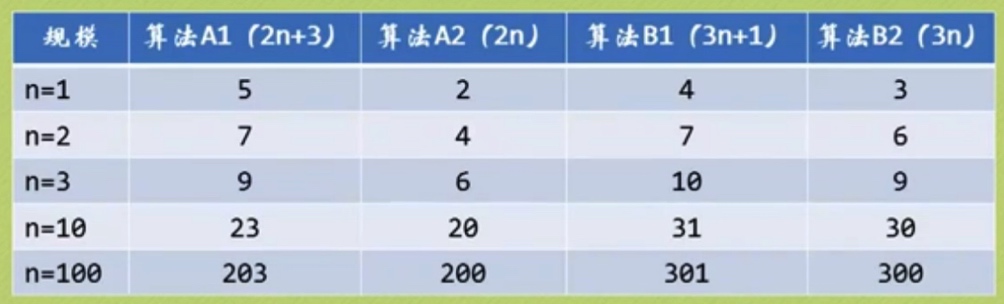
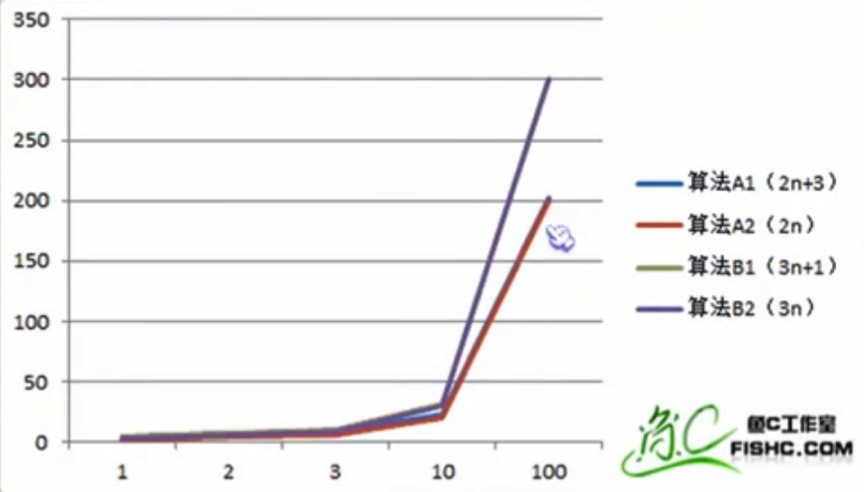
总结：

当n=1时，算法A1效率不如B1；

当n=2时，算法A1效率和B1相同；

当n>2时，算法A1效率开始优于B1；随着n的继续增加，效率逐步拉大；而方程后面的常数基本上可以忽略。

所以：总体上算法A1比B1优秀。

4: 分析忽略的原因 n和n2 的故事

我们来测试一下算法A和B哪个更好？

C1: y=4n+8 C2: y=n

D1: y=2n2 +1 D2: y=n2

我们来看图来分析：





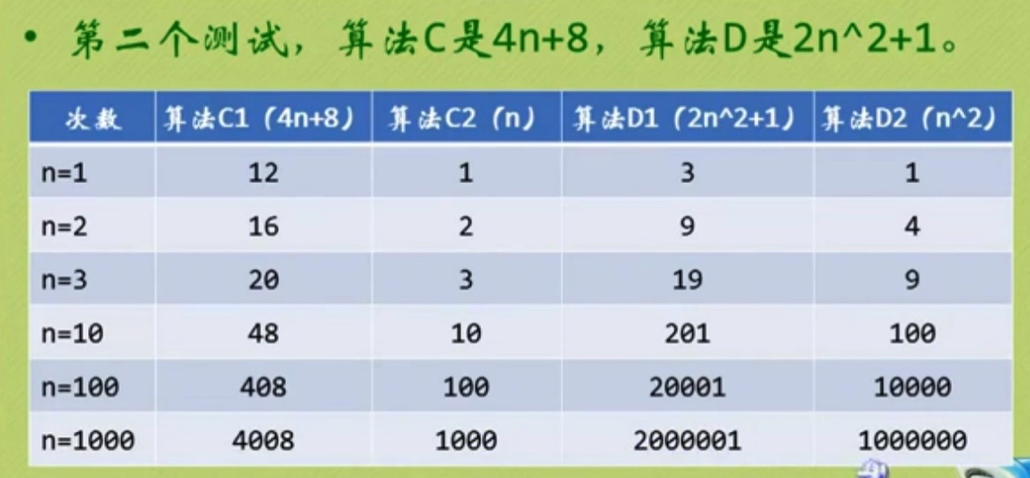
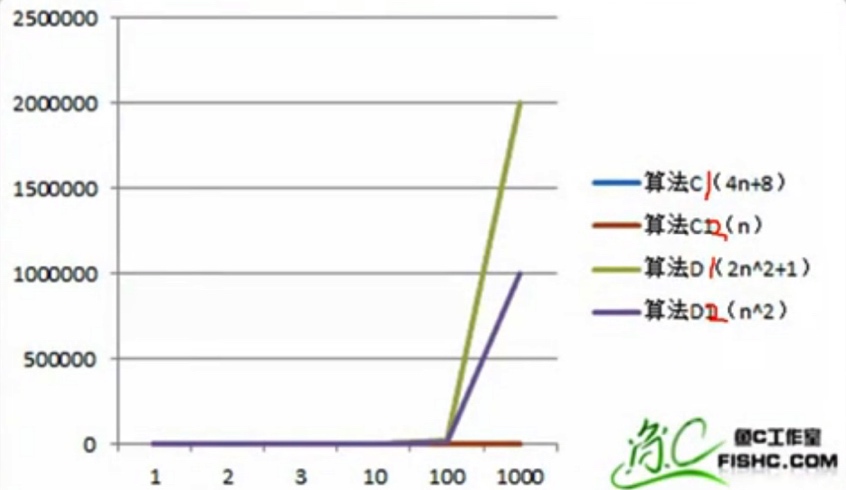
明显发现：

算法C1和C2基本上趋近一条相同的直线。

算法D1和D2相对于言比较明显，远大于C1和C2。

所以：总体上算法C1和C2 在 D1和D2面前，表明C算法变量X前面的常数基本可忽略不计。

5: 分析忽略的原因 n2 和n3 的故事

我们来测试一下算法A和B哪个更好？

E1: y=2n2 +3n+1 E2: y=n2

F1: y=2n3 +3n+1 F2: y=n3

我们来看图来分析：





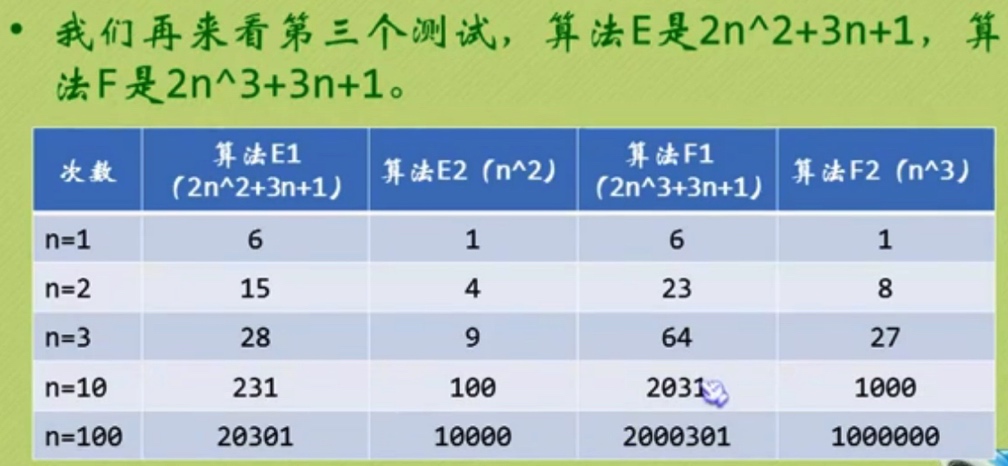
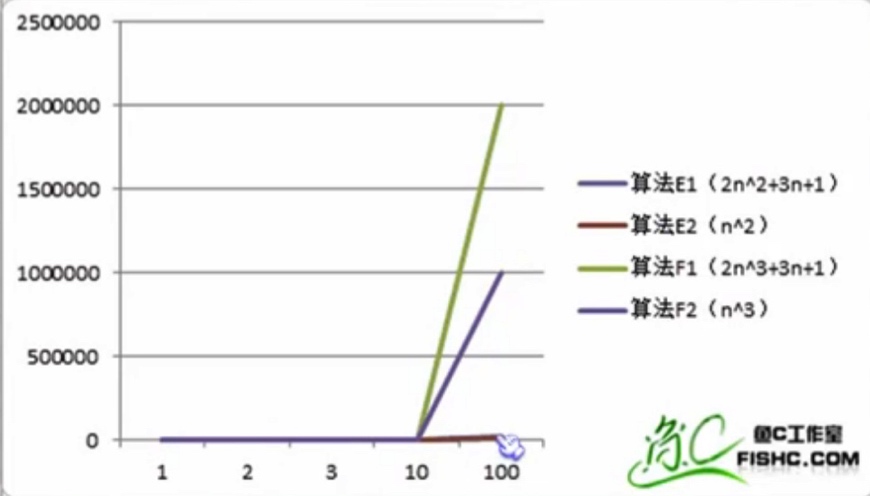
明显发现：

算法E1和E2基本上趋近一条相同的直线。

算法F1和F2相对于言比较明显，远大于E1和E2。

所以：总体上算法E1和E2 在 F1和F2面前，表明E算法变量X前面的常数基本可忽略不计。

6: 分析忽略的原因 n 、 n2 和n3 的故事

我们来测试一下算法A和B哪个更好？

G: y=2n2

H: y=3n+1

I: y=2n2 +3n+1 F2: y=n3

我们来看图来分析：







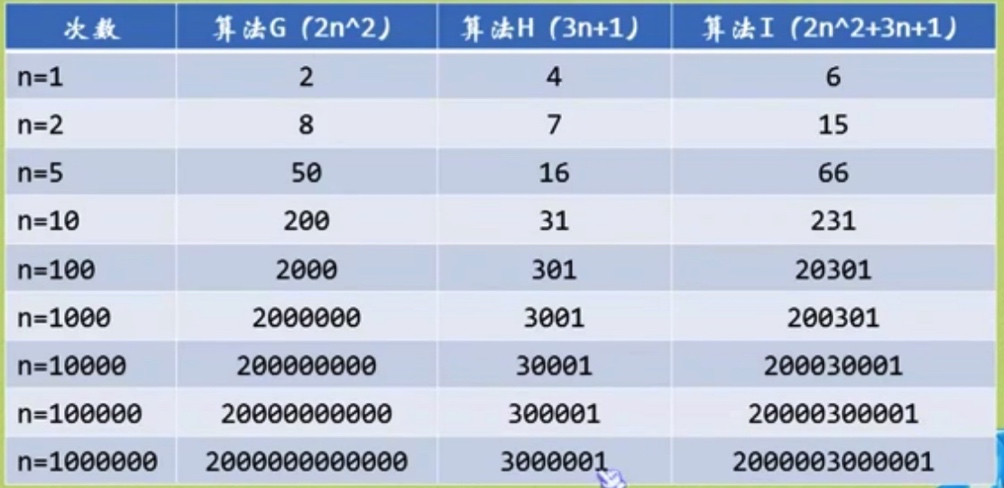
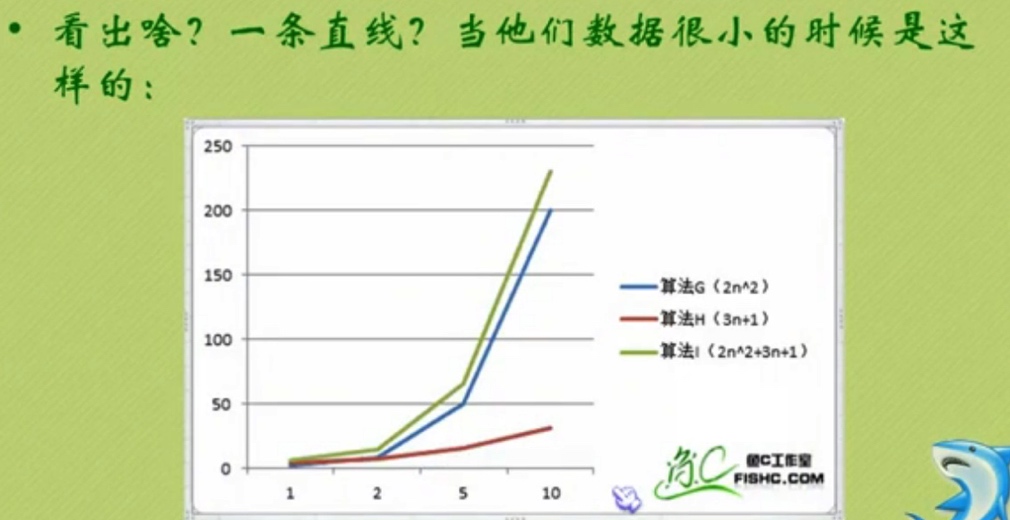
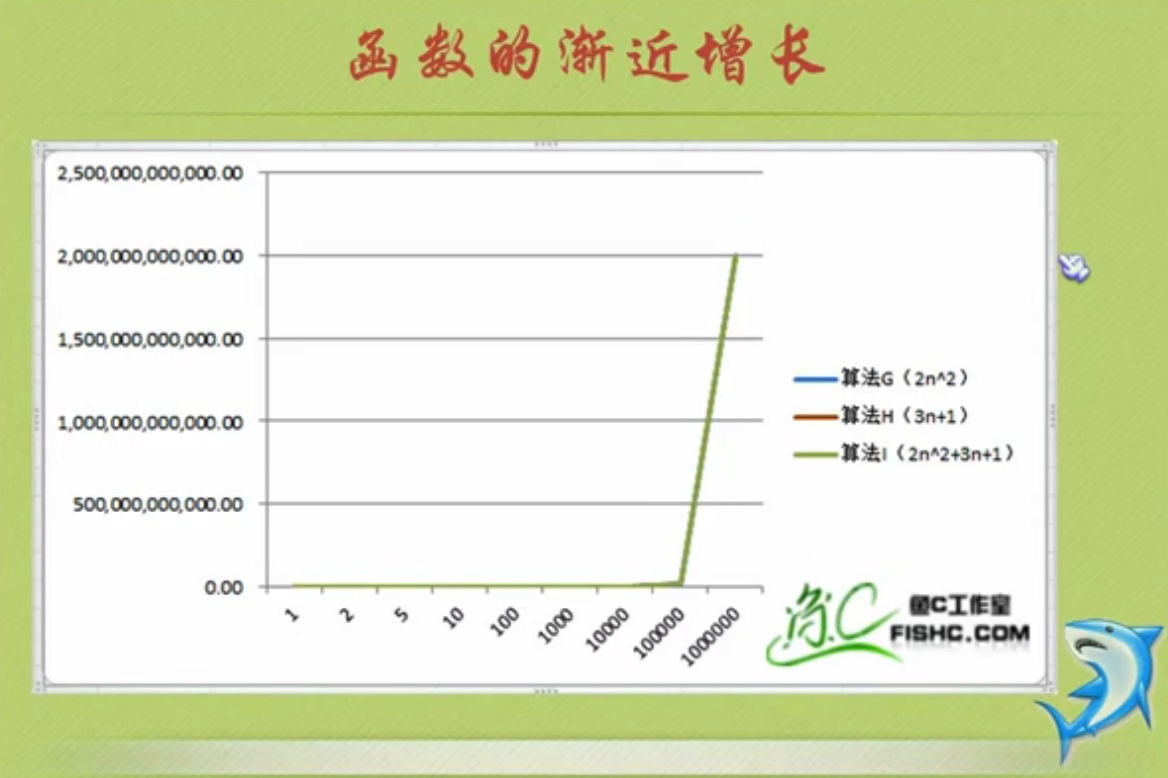
明显发现：

算法G和I基本上趋近一条相同的曲线。

所以：总体上算法在高次项面前，低次项基本可忽略不计。

1.在判断一个算法的效率时，我们应改关注 主项(最高项)的阶数；常数项和低次项常常可以忽略。

2.判断一个算法好不好，我们只通过少量的数据是不能做出准确判断的，很容易以偏概全

2.算法时间复杂度

1.概念

各种装逼术语，可忽略.. 需铭记： 执行次数＝时间 就行

时间复杂度的计算公式：

T(n)=O(f(n))

n表示问题规模

f(n)表示问题规模n的某个函数



2.符号表示 和 最优算法

大写的 O() 来表示算法时间复杂度的记发，我们称之为大O记法。

一般情况下，随着输入规模n的增大， T(n)增长最慢的算法称为最优算法。

我们三个求和算法的时间复杂度分别为：O(1), O(n), O(n2 )



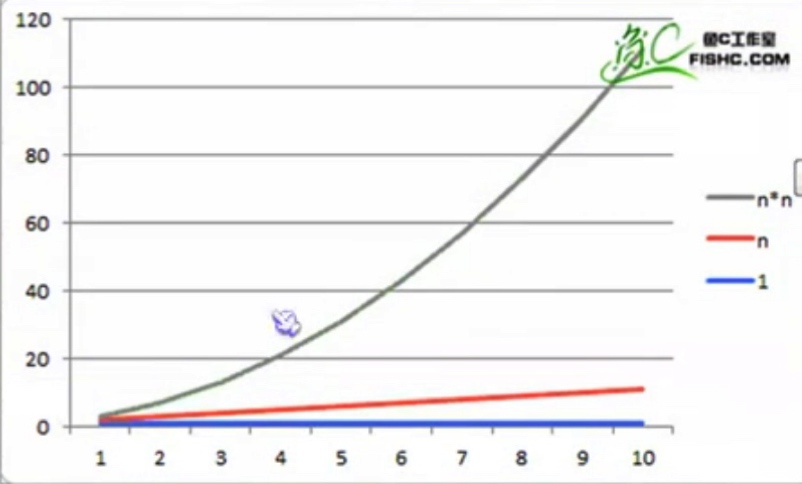
3.推导大O阶，整理以下攻略

1.攻略如下：

－用常数1取代运行时间中的所有加法常数。

－在修改后的运行次数函数中，只保留最高阶项。

－如果最高阶项存在且不是1，则去除与这个项相乘的常数。

－得到的最后结果就是大O阶

例如： y=2n2 +3n+1 最高阶 O(n2 )

2.常数阶－案例如下：



O(8)? 很多初学者常常犯这个错误。

分析如下：

按照概念： T(n)是关于问题规模n的函数。

没错，跟问题规模有关，跟其他的表亲戚都没关系。

所以： 我们记做 O(1) 就可以。(当然可以参考上述攻略)

————————————————————————————————————————————

我想起我的回北京以后的一次面试，问我时间复杂度，我傻逼了一回。

当时什么都不懂，只是很单纯的以为是次数的问题。

2.线性阶－案例如下：

线性阶：就是随着问题规模n的扩大，对于计算次数呈直线增长。

时间复杂度： O(n)



3.平方阶－案例如下：

平方阶：就是随着问题规模n的扩大，对于计算次数呈指数是2的乘方增长。

时间复杂度： O(n2 )

如果是 m层嵌套，就是 O(nm )



如果嵌套循环的次数不相同呢？

当i＝0， j循环n

当i＝1， j循环n-1

...

当i＝n-1， j循环1

结果： y=n+(n-1)+...+1= n(n+1)/2

根据攻略：

时间复杂度：O(n2 )

例如：



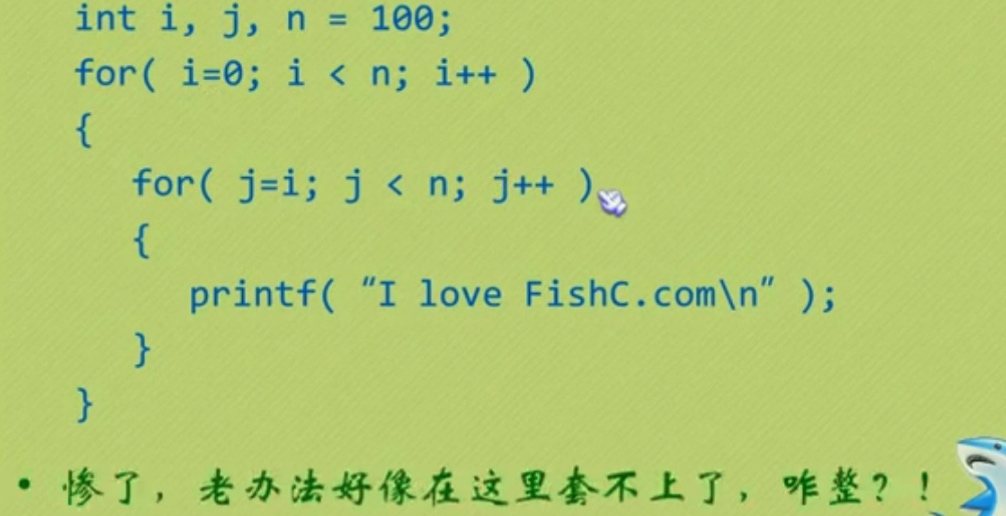
4.对数阶－案例如下：

对数阶：就是随着问题规模n的扩大，对于计算次数呈指数增长。

由于： 2x =n

所以： x = log(2)n

时间复杂度： o(logn)



3.函数调用的时间复杂度分析

1.考考大家学习情况

function时间复杂度： O(1)

整体的书简复杂度： O(n)



2.修改function的时间复杂度

思路：n表示常数。

count=1, 循环 n-1

...

count=n-1, 循环 1

总共：1+...+n-1 = n*(n-1)/2

整体的书简复杂度： O(n2 )



3.组合函数

公式： 0+n2 +n2 = 2n2

时间复杂度: O(n2 )



4.汇总： 常见的时间复杂度

想象一下：指数增长多块，意味着对数增长多慢。

汇总表



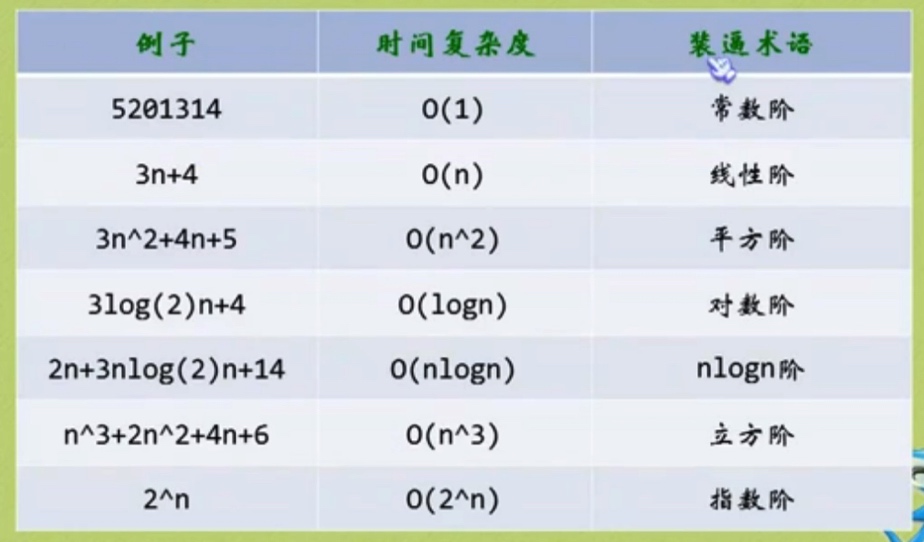
图形表：





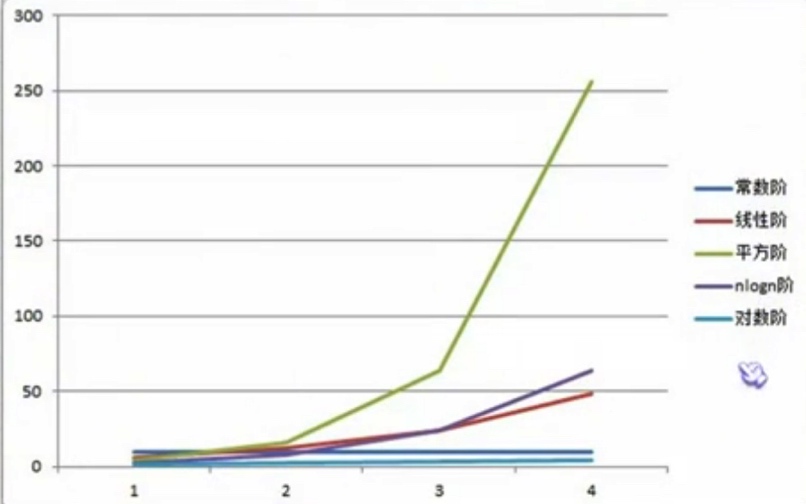
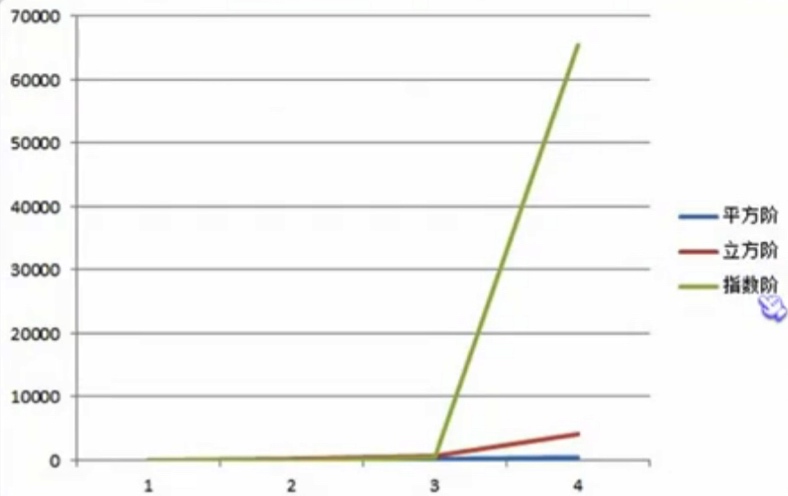
时间复杂度从小到大依次是：

O(1)< O(logn)< O(n)< O(nlogn)< O(n^2 )< O(n^3 ) < O(2^n )< O(n!) < o(n^n )

至于 O(nlogn)在后续博客中会写到。

可以想象：O(n3 )以后的， n值增长后结果会大的难以想象。

4.算法时间复杂度分析：最坏情况和平均情况



一般我们工作中，运行时间是指： 最坏情况的运行时间。

例如：

算法的时间复杂度: 最好是O(1),最坏是O(n),那么时间复杂度就是O(n)

5.算法空间复杂度

例如：要判断 今年是否是闰年？

时间复杂度： 可以是O(1), 我可以把数全部存到数组中。

空间复杂度： 就是O(n) 线性增长。

用空间来换取时间开销的小技巧，不过得分场景。

空间复杂度的计算公式：

S(n)=O(f(n))

n为问题的规模

f(n)为语句关于n所占存储空间的函数

常说的复杂度：通常都是指 时间复杂度；并且时间复杂度才是算法的潮流。