怎么架构网站/汨罗网站seo

随机变量:随机变量(random variable)表示随机试验各种结果的实值单值函数。随机事件不论与数量是否直接有关,都可以数量化,即都能用数量化的方式表
概率:,它反映随机事件出现的可能性(likelihood)大小
概率分布:是指用于表述随机变量取值的概率规律,分布形状
概率分布包括:离散概率分布(概率质量函数PMF),连续概率分布(概率密度函数PDF)
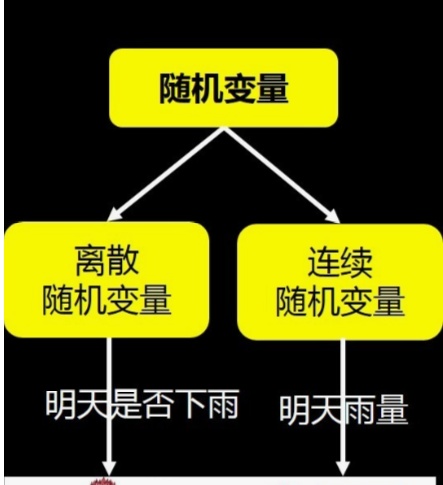
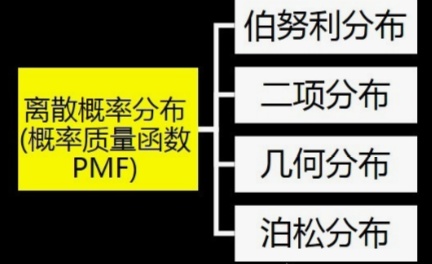
离散概率分布:伯努利分布,二项分布,几何分布,泊松分布
连续概率分布:幂律分布,正态分布
- 伯努利分布Bernoulli DIstribition
- 二项分布Binnomial Distribution
- 几何分布Geometric Distribution
- 泊松分布Poisson Distribution
- 正态分布Normal Distribution
学习思路:有什么用—如何检验—如何计算—Python实现
1.伯努利分布Bernoulli DIstribition(抛硬币概率)
特征:1.进行一系列相互独立的试验
2.每次实验都只会出现两种可能,成功或失败
3.单次试验成功的概率相同。
Python实现 :stats.bernoulli.pmf(X, p)

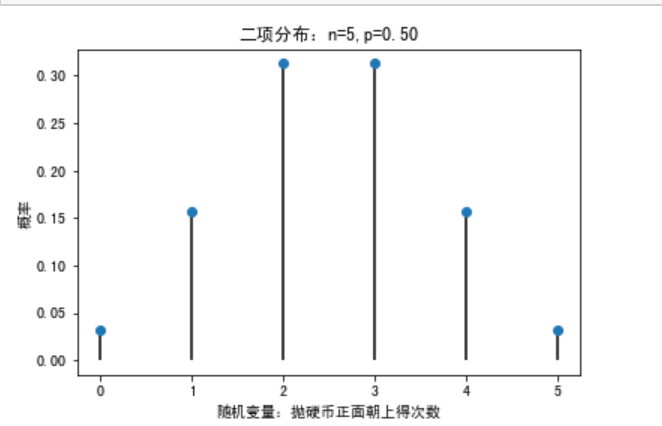
2.二项分布Binnomial Distribution(抛硬币5次中2次正面朝上的概率)
特征:1,进行一系列相互独立的试验
2,每次实验都只会出现两种可能,成功或失败
3,单次试验成功的概率相同。试验次数有限
4,感兴趣的是在有限试验次数内,获得成功的次数

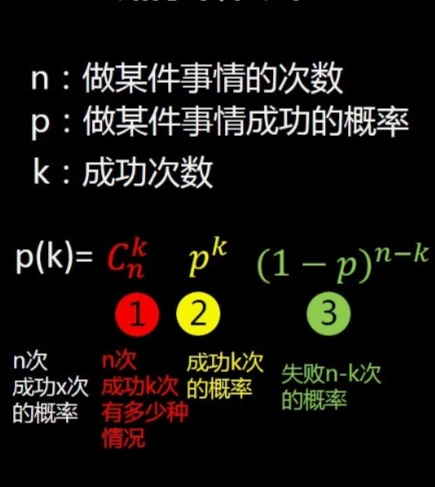
Python实现plist=stats.binom.pmf(X,n,p)
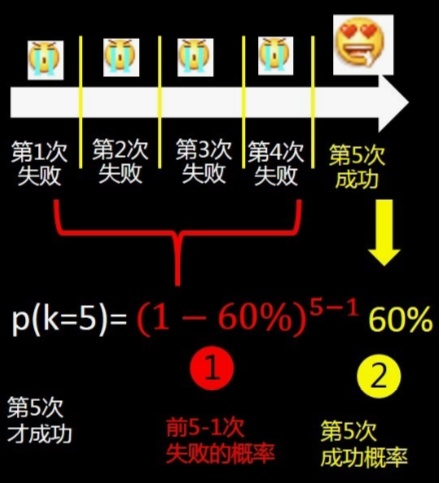
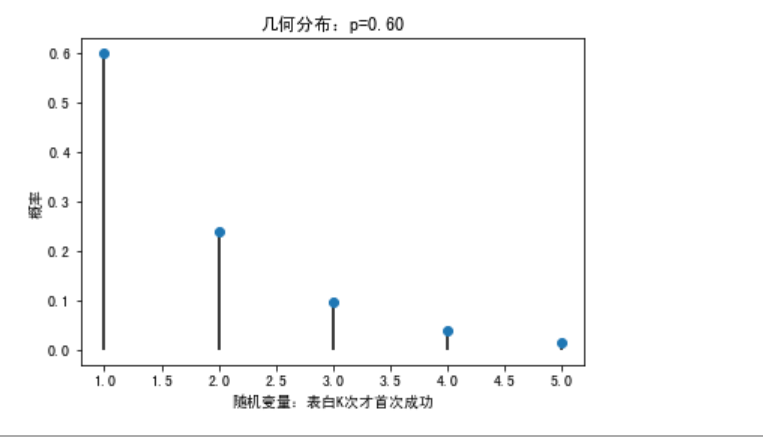
3.几何分布Geometric Distribution (表白K次中第一次成功的概率)
特征:1,进行一系列相互独立的试验
2,每次实验都只会出现两种可能,成功或失败
3.单次试验成功的概率相同
4.感兴趣的是,为了取得第一次成功需要进行多少次试

Python实现:plist=stats.geom.pmf(X,p)
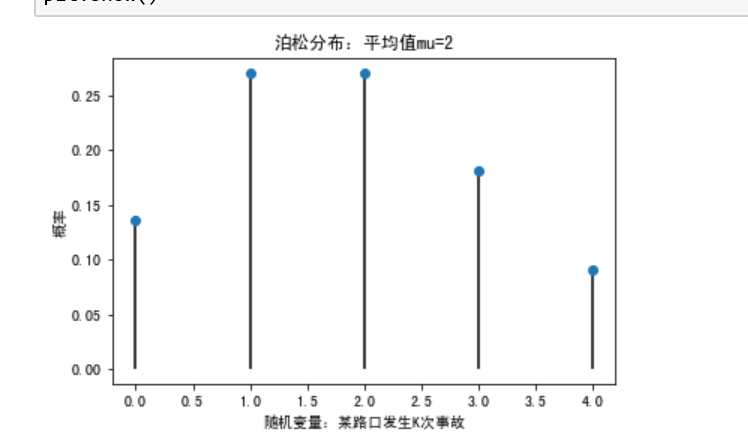
4.泊松分布Poisson Distribution (每天发生两次车祸的概率)
特征:1.单独事件在给定区间内随机、独立的发生
2.已知该区间内的事件平均发生次数,且为有限数值
3.感兴趣的是给定区间内事件发生的次数

Python实现:plist=stats.poisson.pmf(X,mu)
数据涵盖的是一个范围,这个范围内的任何一个数值都有可能成为事件结果。对于离散概率分布,我们关注的是取得一个特定数值的概率;而对于连续概率分布来说,我们关心的是取得一个特定范围的概率。
用概率密度函数来描述连续随机变量的概率分布。为了求特定数值范围内的概率,首先可画出概率密度函数,位于函数图形下方且介于这个特定数值范围之间的面积就是这个特定数值范围的概率
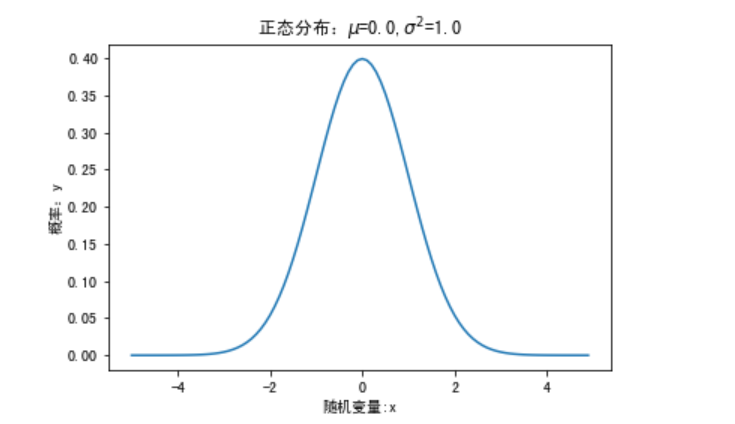
5.正态分布Normal Distribution
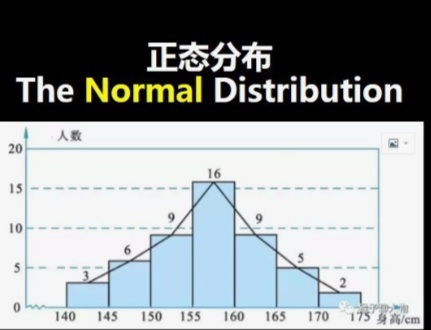
Python实现:y=stats.norm.pdf(X,mu,sigma)
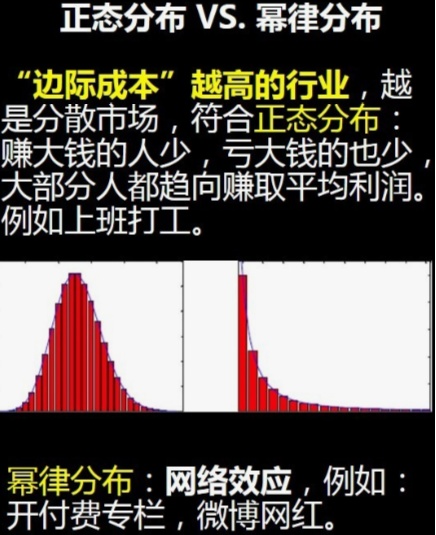
查找概率值:确定概率范围—算出标准分—查找Z表格
