当前位置：首页 > news >正文

松江品划做企业网站/中国十大seo

news 2025/6/30 0:00:11

松江品划做企业网站,中国十大seo,wordpress 太多重定向,阳泉市建设局网站如果你有使用过诸如PyTorch，Flux/Tracker，AutoGrad这一类基于运算符重载的自动微分库，就会发现，这些库有两个通病：只能使用框架所提供的函数和矩阵/张量类型，如果想要对一般的程序进行求导就不行了无法处理…

如果你有使用过诸如PyTorch，Flux/Tracker，AutoGrad这一类基于运算符重载的自动微分库，就会发现，这些库有两个通病：

只能使用框架所提供的函数和矩阵/张量类型，如果想要对一般的程序进行求导就不行了
无法处理控制流，因为简单的运算符重载无法记录下来控制流

在Yan LeCun等人的号召下，想要实现可微分编程(Differentiable Programming)如果没有上面这两个功能可不行。不能对控制流进行微分叫什么可微分编程？因为我们希望我们编写的任意在数学上成立的程序都可以进行自动微分。此外上篇文章的评论区里有人提到了TensorFlow的自动产生符号导数然后加入计算图的功能。而实际上如果对编译器数学的同学会知道这类符号计算就是一个简单的编译步骤。

这些问题在源对源(source to source)的自动微分下实现起来将非常自然，这篇文章将实现一个不带控制流的简单版本，而完整的版本已经在Julia中通过staged programming的方式实现了，这个包叫做 Zygote.jl 。它中文翻译很搞笑，叫卵子。使用这个包的人都用了个卵子自动微分。我在今年JuliaCon的周五Hackthon期间在Zygote的作者Mike的帮助下实现了一个简单版本的。

不过，在我们开始编写程序前，让我们来回顾一些基础知识。

Julia语言的编译过程

首先让我们来简单了解一下Julia语言是如何进行编译的。

首先，所有的代码本质上都是一些字符串(string)，存储在硬盘上的文本文件中
我们首先要解析(parse)这些字符串，得到一个抽象语法数(Abstract Syntax Tree，AST)
而 AST 里有一些节点是宏，这些宏是一些只接受编译时期变量的，里面描述了如何产生更多的 AST，在这一步将会运行这些宏，我们成为展开AST。你可以通过 macroexpand 宏查看这一步的编译结果
这个时候我们再将AST里的语法糖等节点全部替换为函数调用，并且使用SSA(Static Single Assignment)形式的IR作为更低级的表示。什么是SSA IR？我们将在后面介绍

到此位置我们完成了代码的初始化过程。

然后我们的函数会在被派发的时候才会被继续编译，这是因为对于一般的函数(generic function)我们是无法在编译时期就确定这个函数的变量类型的，从而无法产生定制的机器码。例如对机器来说 Int 和 Float64 即便都是加法，对整数来说调用的可能是 leaq 指令，而浮点数则可能是 vaddsd
然后我们开始进行类型推导(type inference)，这是为什么你可以不用写清楚到底是什么类型的原因。同时有了类型以后编译器才能做很多优化。这样我们就得到了带类型的IR(typed IR)，你可以用 code_typed 来查看这部分编译结果
然后我们用这个IR来产生LLVM IR
LLVM IR会用来产生机器码，你可以用 code_native 宏来获得这个编译结果

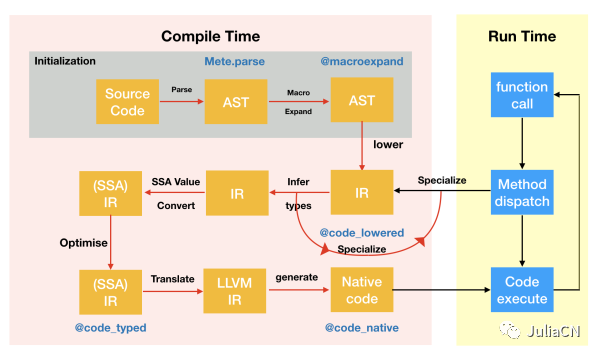
为了描述Julia是如何编译的，我从之前的JuliaCon的报告里拿出来一副图。

这张图更清楚一些，你可以看到与静态语言不同的是，每次函数调用都会经过编译过程。Julia中的编译(包括JIT编译)是以函数调用为界的。

SSA格式的中间表示

完整的介绍SSA需要很大的篇幅，足够写一本书了。但是不用担心，我们这里需要用到的部分很简单。你只需要知道下面几个概念就可以了

所有的变量都有且仅有一次赋值(有时候也会说这个是线性的)
大部分变量的值都来自于某个函数的调用(function call)
控制流都变成了分支语句(branching)

如果你已经阅读过我上篇文章，我相信你已经了解计算图这个概念，但是现在我们要重新思考什么是计算图。我们回顾一下上一节用到的图

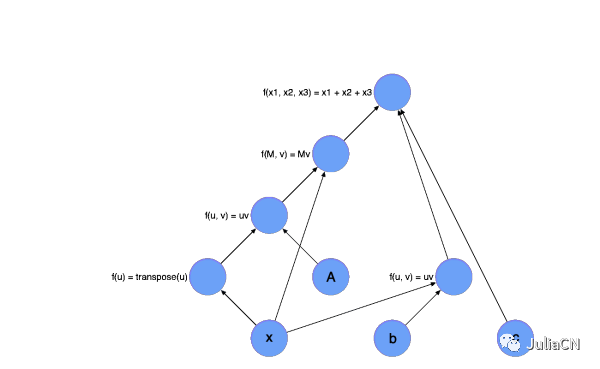
在进行AD的计算的时候，我们将计算过程表示为一个计算图。每个节点都会使用一个运算符(operator)然后获得一个中间值(一个节点)，接下来这个节点的值会和函数一起暂时存起来，在后向传播的时候使用。也就是说每个节点的中间变量都只会被赋值一次，否则就不能唯一对应一个算符。而每个节点有两个函数，一个是代表前向计算的函数，另外一个则是代表后向传播的导数函数。

很自然的，我想你已经发现了，这就是一个SSA的格式。而所谓的自动微分，其实就是我们正常的前向程序的某一个对偶的程序(也就是一个对偶的函数)。而实际上，没有控制流的计算图我们称之为 Wengert Lists 。大部分基于运算符重载的自动微分实际上都是实现了这个算法，有时候它也被称为Tape。而SSA格式则更加一般，它包含了控制流。所以我们可以通过对SSA格式来计算自动微分来实现对控制流的自动微分。这也是Zygote第一篇文章所提到的方法。

而由于后向传播的函数只是前向传播的函数的伴随(adjoint，实际上一些数学家也认为后向传播可以定义在一个对偶空间上，所以我们不妨就使用这个称谓)。我们不妨直接将这个函数写做一个前向传播函数+一个闭包的格式。

function forward(::typeof(your_function), xs...)# function declaration
    output = # function output
    output, function (Δ)# a closureendend

实现成闭包的好处是实现一些需要使用前向传播的中间值的导数的时候我们可以把这些中间值以闭包函数的状态(state)的方式托管给编译器，而不需要像我在上篇文章里一样，手动将其存在一个Node对象中。我们称这个返回的闭包函数为pullback。

所以假如我们想要获得一个下面这个函数的导数

function foo(x)
    a = bar(x)
    b = baz(x)return bend

如果手动做这件事情，我们只需要定义一个 forward 函数

function forward(::typeof(foo), x)
      x1, back1 = forward(baz, x)
      x2, back2 = forward(bar, x1)return x2, function (Δ)
         dx1 = back2(Δ)
         dx2 = back1(dx1)return dx2endend

实际上，一般的来说，一段没有控制流的程序的伴随，就是倒着把这段程序中的所有函数调用换成伴随程序的调用，变量换成其对应的伴随变量(adjoint variable)。但是我们如何通过一个函数定义来产生这个forward函数呢？有人可能会说宏，但是宏会要求我们在所有可以进行求导的函数前面都要这样标记，这是我们不希望的，我们希望未来使用这个自动微分的时候我们不需要写任何额外的东西。

而由于SSA格式的IR已经将所有的语法糖，函数都转换成低级表示了，这也就意味着仅仅需要定义一些原始表示，我们就可以用上面这个规则(实际上就是链式法则)组合出非常多的导数，而这些导数的生成都发生在编译时期，所以不会反复占用运行时间，并且这也能帮助我们未来进一步进行一些有针对性的优化。

所以我们想在SSA IR上来做这件事，但是怎么做呢？我们知道宏可以用来修改代码的解析过程(parsing)，而Julia里还有另外一个元素用来实现对类型推导和IR的修改，生成函数(generated function)。生成函数可以通过一个宏来声明

@generated function foo(a, b, c)return :(1 + 1)end

它看起来像是一个普通函数，但是注意它是发生在类型推导期间的

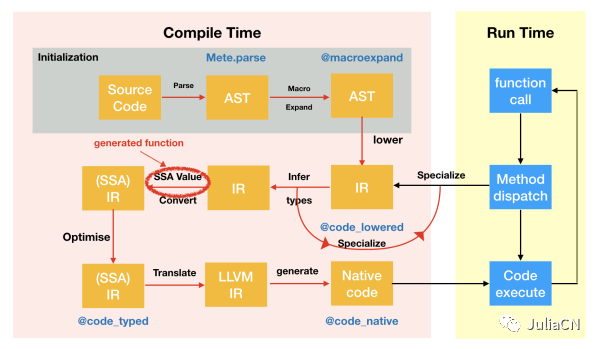
所以你只能知道函数变量 a, b, c的类型信息，我们可以通过类型信息产生两种格式的代码，一种是AST表达式，在Julia里叫Expr，另外一种就是我们的SSA IR，是一种叫CodeInfo的Julia对象。IRTools里提供了操作SSA IR的一些工具，我们将使用这个包来编写产生这个forward函数的代码。

我们可以通过 code_ir 宏来拿到函数的ir对象，这个对象是被IRTools处理过的，它的类型是IR。和 code_typed 宏或者 code_lowered 宏得到的对象不同的是，IR类型实现了一些方便的函数操作，并且IR类型中不会保存变量的名称，所有的变量都用 %数字来表示

julia> @code_ir foo(1.0)1: (%1, %2)%3 = (Main.baz)(%2)%4 = (Main.bar)(%3)return %4

注意，你会发现，即便这里 baz和bar这两个函数没定义也不会报错，这是因为Julia本质上还是一个动态语言，所以只要在真正运行的时候才会报错。

这个格式下，每一行代码都绑定了一个变量，等号右边我们称之为声明(statement)，左边是变量(variable)。你可以用类似字典的接口来使用这个对象，例如

julia> using IRTools: var
julia> ir[var(3)]
IRTools.Statement(:((Main.baz)(%2)), Any, 1)

它会给你一个声明对象，这个对象里记录了这段声明的表达式，这个宏给你的是没有经过类型推导的IR。所以后面的Any就是这个变量的类型。Any也是Julia中唯一的静态类型。为了简单起见，我们这里不介绍带类型的IR(因为原理上是类似的但是实现细节有一些不同)。最后数字1是指这段声明所在的行号。

前面的1是什么意思呢？在SSA格式中我们用这样的代码块来表示分支，我们不妨写一个ifelse语句看看

julia> function foo(x)if x > 1
               bar(x)else
               baz(x)endend
foo (generic function with 1 method)
julia> @code_ir foo(1.0)1: (%1, %2)%3 = %2 > 1
  br 3 unless %32:%4 = (Main.bar)(%2)return %43:%5 = (Main.baz)(%2)return %5

ifelse在低级表示中是通过branch语句表示的，实际上循环也是类似的。Julia里的循环只是对iterate函数的语法糖而已。所以我们只要能够对br语句进行微分，我们就可以对控制流微分了。

julia> function foo(x)for x in 1:10
               bar(x)end
           baz(x)end
foo (generic function with 1 method)
julia> @code_ir foo(1.0)1: (%1, %2)%3 = 1:10%4 = (Base.iterate)(%3)%5 = %4 === nothing%6 = (Base.not_int)(%5)
  br 3 unless %6
  br 2 (%4)2: (%7)%8 = (Core.getfield)(%7, 1)%9 = (Core.getfield)(%7, 2)%10 = (Main.bar)(%8)%11 = (Base.iterate)(%3, %9)%12 = %11 === nothing%13 = (Base.not_int)(%12)
  br 3 unless %13
  br 2 (%11)3:%14 = (Main.baz)(%2)return %14

那么这个IR是怎么获得的呢？为了获得IR，我们首先需要知道这个通用函数(generic function)被派发了哪个方法(method)，在Julia里每个通用函数都有一个方法表(method table)你可以通过这个函数的类型标签来获得具体的方法。例如这个foo函数，每次调用 foo(1.0) 的时候，Julia都会产生下面的标签

Tuple{typeof(foo), Float64}

查看全文

http://www.jmfq.cn/news/4897999.html